ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА РФ
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Ростовский государственный университет путей сообщения»
____________________________________________________________
ТЕХНИЧЕСКАЯ ДИАГНОСТИКА ЭЛЕМЕНТОВ И СИСТЕМ
Учебно-методическое пособие к практическим работам по дисциплине «Основы технической диагностики»
Ростов-на-Дону
2014
УДК 621.331:621.3.019.3:629.4
Техническая диагностика элементов и систем: учебно-методическое пособие к практическим работам // Ю.Г. Семенов / Рост. гос. ун-т путей сообщения. Ростов н/Д, 2014. – 36 с.
Учебно-методическое пособие предназначено для проведения практических работ по дисциплине, предметом которой являются основы технической диагностики объектов и систем. Пособие содержит варианты индивидуальных заданий, направленных как на аудиторную, так и на самостоятельную работу студентов, а также методические материалы для решения предлагаемых задач. Предназначены для студентов специальности 190901 «Системы обеспечения движения поездов». Могут быть использованы для проведения занятий со студентами всех форм обучения, а также служить в качестве задания на расчетно-графические и контрольные работы.
Табл. 20 Библ.: 7 назв.
Составитель:
канд. тех. наук Ю.Г. Семенов, доц. кафедры «Автоматизированные системы электроснабжения»
Рецензент:
доктор технических наук, проф. Соломин В.А. (РГУПС)
© Ростовский государственный университет путей сообщения, 2014
Содержание
Стр.
4
5
5
8
11
13
16
16
17
18
18
21
22
25
29
30
ВВЕДЕНИЕ….………………………………………………………………………
Вероятностные методы распознавания состояний объекта………............
Определение вероятностей состояний системы, представленной структурной схемой по надежности…………………………………….................
Определение состояния системы методом Байеса ………………...............
Определение достоверности и ошибок диагностики…………....................
Оптимальные статистические решения о состоянии объекта…..................
Прогнозирование состояния объекта и определение момента начала профилактики……………………………………………………………………
Вероятностное прогнозирование состояния при непрерывном изменении диагностического признака………………………………………………………....
Вероятностное прогнозирование состояния при дискретном изменении диагностического признака........................................................................................
Диагностика объектов, представленных функциональной моделью………..
Функциональная модель и таблица неисправностей………………………
Логический алгоритм локализации неисправности…………...……….......
Информационный алгоритм локализации неисправности………………...
Условные программы и стоимость диагностики …………………………..
Рекомендуемая литература…………………………………………………...…….
Приложения…………………………………………………………………...…......
Введение
Учебно-методическое пособие направлено на выработку и закрепление у студентов знаний и навыков по основам диагностики технических элементов и систем. Решение задач, приведенных в настоящих методических указаниях, требует предварительного изучения лекционного материала, а процесс решения – использования учебной [1, 2, 3] и справочной литературы [4]. Задачи, предлагаемые для решения, используют вероятностный подход к решению задач диагностики, как наиболее общий. Ряд задач, требующих большого объема или цикличности вычислений, могут быть решены с применением персональных ЭВМ с использованием компьютерных программ Excel или Mathcad. Задачи содержат индивидуальные данные для расчета, определяемые трехзначным кодом, задаваемым каждому студенту индивидуально. Номер схем выбирается по порядковому номеру в журнале учебной группы. Объем решений рассчитан как на аудиторную, так и на самостоятельную работу студентов. Материалы, изложенные в методических указаниях, позволяют формировать различные варианты заданий для выполнения расчетно-графических или контрольных работ. Пособие снабжено несколькими примерами расчета и справочными таблицами, заимствованными из [4] и необходимыми для численного решения ряда задач.
Вероятностные методы распознавания состояний объекта
Определение вероятностей состояний системы, представленной структурной схемой по надежности
Технические объекты могут быть представлены в виде структурных схем по надежности. Такие модели объектов используются для решения задач диагностики тогда, когда отсутствуют или нет возможности получить опытные данные об априорных вероятностях состояния объекта, необходимых в дальнейшем для использования вероятностных методов с целью постановки различных диагнозов объекта. Первой задачей диагностики является определение всего множества N состояний объекта и разбиение множества на подмножества работоспособных N1 и неработоспособных N2 состояний. При этом в рамках работоспособного состояния системы могут присутствовать функциональные состояния N3, означающие наличие скрытого (неявного) дефекта в системе. Следует учитывать вероятностный характер отказов отдельных блоков в объекте, а также то, что в объекте могут отказать как один блок, так и несколько блоков одновременно.
В задаче объект представлен одной из структурных схем, которая задается таблицей П1. Номер схемы задается в виде первого двузначного кода в скобках (XY). Значения вероятностей отказа отдельных блоков приведены в табл.1.1. Значения вероятностей выбираются по второму двузначному коду в скобках (VZ). Таким образом, задание для выполнения данной задачи представляется в виде (XY)-(VZ).
Предполагается:
отдельные блоки независимы по надежности;
в общем случае возможен одновременный отказ нескольких блоков;
известны на данный момент времени вероятности отказов отдельных блоков q1, q2, q3, q4, …, qn.
Требуется привести расчетную схему, определить общее количество N состояний объекта, подмножество работоспособных N1 и неработоспособных N2 состояний, а также вероятности каждого из состояний и вероятности неработоспособного и работоспособного состояний объекта. Определить тип состояний системы: с явной или неявной неисправностью, а также рассчитать вероятности состояний системы при наличии указанных неисправностей.
Ниже рассматривается пример решения задачи для схемы модели объекта, представленной на рис.1.1. Объект имеет n = 3 блока.
Рис.1.1. Пример структурной схемы модели объекта
Таблица 1.1
Вероятности отказов блоков и номер схемы
Номер схемы, код (XY) |
01 |
02 |
03 |
04 |
05 |
06 |
07 |
08 |
09 |
10 |
11 |
12 |
Код (VZ) |
01 |
02 |
03 |
04 |
05 |
06 |
07 |
08 |
09 |
10 |
11 |
12 |
q1 |
0,28 |
0,26 |
0,21 |
0,25 |
0,3 |
0,28 |
0,1 |
0,11 |
0,11 |
0,23 |
0,2 |
0,08 |
q2 |
0,1 |
0,24 |
0,3 |
0,18 |
0,18 |
0,16 |
0,12 |
0,29 |
0,2 |
0,1 |
0,23 |
0,28 |
q3 |
0,25 |
0,22 |
0,2 |
0,27 |
0,2 |
0,31 |
0,3 |
0,23 |
0,26 |
0,34 |
0,3 |
0,1 |
q4 |
0,27 |
0,1 |
0,16 |
0,2 |
0,11 |
0,12 |
0,3 |
0,21 |
0,32 |
0,21 |
0,14 |
0,35 |
q5 |
0,1 |
0,18 |
0,13 |
0,1 |
0,21 |
0,13 |
0,18 |
0,16 |
0,11 |
0,12 |
0,13 |
0,19 |
Номер схемы, код (XY) |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
Код (VZ) |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
q1 |
0,12 |
0,21 |
0,22 |
0,12 |
0,32 |
0,31 |
0,35 |
0,1 |
0,2 |
0,17 |
0,12 |
0,23 |
q2 |
0,31 |
0,27 |
0,28 |
0,22 |
0,18 |
0,11 |
0,25 |
0,18 |
0,09 |
0,11 |
0,25 |
0,19 |
q3 |
0,17 |
0,09 |
0,16 |
0,24 |
0,13 |
0,26 |
0,14 |
0,24 |
0,2 |
0,22 |
0,22 |
0,29 |
q4 |
0,2 |
0,26 |
0,1 |
0,11 |
0,22 |
0,13 |
0,1 |
0,33 |
0,22 |
0,2 |
0,21 |
0,1 |
q5 |
0,2 |
0,17 |
0,24 |
0,31 |
0,15 |
0,19 |
0,16 |
0,15 |
0,29 |
0,3 |
0,2 |
0,19 |
Задача решается в следующем порядке.
Определяется общее количество возможных состояний объекта:
N = 2n.
Составляются варианты состояний объекта с работающими и отказавшими блоками; в таблицу заносится условный код в виде «1» при работающем блоке и в виде «0» – при неработающем блоке.
Рассчитываются вероятности каждого из N состояний при условии независимости отдельных блоков:
,
где Si – i-е состояние объекта; j – номер отказавшего блока, j = 0, 1, 2, …, n; k – номер работающего блока, k = 0, 1, 2, …, n; k j; k + j = n.
Определяются работоспособные N1 состояния объекта, когда при различных состояниях блоков на общем выходе объекта присутствует правильный выходной сигнал y.
Определяется неработоспособные N2 состояния объекта, когда при различных состояниях блоков на общем выходе объекта правильный выходной сигнал y отсутствует.
Определяется тип неисправности объекта:
явная неисправность, когда объект полностью потерял работоспособность;
неявная (скрытая) неисправность, когда объект не потерял работоспособность, но в нем присутствует отказавший блок.
Из числа работоспособных состояний N1 выделяются неисправные, но работоспособные состояния N3 и рассчитывается вероятности такого состояния:
.
Определяется безусловная вероятность соответственно работоспособных и неработоспособных состояний объекта:
;
.
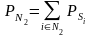Определяется безусловная вероятность неисправного состояния объекта с явными и неявными неисправностями:
,
Определяется безусловная вероятность исправного состояния объекта:
,
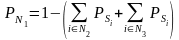Результаты расчетов сводятся в табл.1.2. и 1.3.
Таблица 1.2
Таблица результатов расчета *
Состояние системы Si |
Состояние блоков |
Формула PSi |
Значение PSi |
Ni |
Тип неисправности |
||||||
1 |
2 |
3 |
|||||||||
S0 |
1 |
1 |
1 |
(1-q1)(1-q2)(1-q3) |
0,28 |
N1 |
Нет |
||||
S1 |
0 |
1 |
1 |
q1(1-q2)(1-q3) |
0,07 |
N2 |
Явная |
||||
S2 |
1 |
0 |
1 |
(1-q1)q2(1-q3) |
0,12 |
N1 (N3) |
Неявная |
||||
S3 |
1 |
1 |
0 |
(1-q1)(1-q2) q3 |
0,28 |
N1 (N3) |
Неявная |
||||
S4 |
0 |
0 |
1 |
q1q2(1-q3) |
0,03 |
N2 |
Явная |
||||
S5 |
1 |
0 |
0 |
(1-q1)q2q3 |
0,12 |
N2 |
Явная |
||||
S6 |
0 |
1 |
0 |
q1(1-q2)q3 |
0,07 |
N2 |
Явная |
||||
S7 |
0 |
0 |
0 |
q1q2q3 |
0,03 |
N2 |
Явная |
||||
*Расчет приведен для вероятностей q1 = 0,2; q2 = 0,3; q3 = 0,5.
В столбце Ni серым цветом отмечены работоспособные, но неисправные состояния системы.
Таблица 1.3
Вероятности состояний объекта
Состояние |
Безусловная вероятность состояния |
Исправное |
0,28 |
Неисправное |
0,07 + 0,12 + 0,28 + 0,03 + 0,12 + 0,07 + 0,03 = 0,72 |
Работоспособное |
0,28 + 0,12 + 0,28 = 0,68 |
Неработоспособное |
0,07 + 0,03 +0,12 + 0,07 + 0,03 = 0,32 |
Неисправное работоспособное |
0,12 + 0,28 = 0,4 |