Impulse – единичный импульс, Filter – фильтр, Impulse Response – импульсная характеристика, Fourier Transform – преобразование Фурье, Frequency Response – частотная характеристика

Если импульсная характеристика фильтра спадает до нуля в течение конечного интервала времени, то такой фильтр называют фильтром с конечной импульсной характеристикой – КИХ (Finite Impulse Response - FIR). Если импульсная характеристика существует на бесконечно большом интервале, то фильтр с такой характеристикой называют фильтром с бесконечной импульсной характеристикой – БИХ (Infinite Impulse Response - IIR). Тип импульсной характеристики: КИХ или БИХ, зависит от способа вычисления выходного сигнала.

Основное различие между КИХ и БИХ фильтрами заключается в том, что у КИХ фильтров выходной сигнал зависит только от текущего и предыдущих значений входного сигнала, а у БИХ фильтров выходной сигнал зависит не только от текущего и предыдущих значений входного сигнала, но и от предыдущих значений выходного сигнала.

Рассмотрим в качестве примера кассовый аппарат в супермаркете. Пусть x[k] у нас будет стоимостью k-го товара, приобретаемого покупателем, причем 1  k N и N – общее количество товаров. Кассовый аппарат складывает стоимость каждого товара, чтобы выдавать промежуточную суммарную стоимость для первых k товаров y[k]:

y[k] =x[k] + x[k–1] + x[k–2] + x[k–3] + … + x[1] (B-2a)

Следовательно, общая стоимость всех товаров будет y[N]. Поскольку у[k] – это стоимость первых k товаров, а y[k–1] – это стоимость первых k–1 товаров, уравнение (B-2a) можно переписать в виде:

y[k] = y[k–1] + x[k] (B-2b)

C учетом налога с продаж 8% уравнения B-2a и B-2b примут вид

y[k] = 1.08x[k] + 1.08x[k–1]

+ 1.08x[k–2] + 1.08x[k–3] + … + 1.08x[1] (B-3a)

y[k] = y[k–1] + 1.08x[k] (B-3b)

Оба уравнения B-3a и B-3b одинаково описывают работу кассового аппарата. Различие заключается в том, что в уравнении B-3a выходной сигнал выражен через значения только входного сигнала, а в уравнении B-3b – через значения и входного, и выходного сигнала. Форму уравнения B-3a называют нерекурсивной (КИХ), а форму уравнения B-3b называют рекурсивной (БИХ).

Коэффициенты фильтра

В левой части уравнения B-3a постоянный множитель при каждом слагаемом равен 1.08, а в левой части уравнения B-3 постоянный множитель при слагаемом y[k–1] равен 1, а при слагаемом x[k] – 1.08. Эти множители называют коэффициентами фильтра. Для БИХ фильтра коэффициенты, на которые умножаются значения входного сигнала, называют прямыми коэффициентами, а те, на которые умножаются значения выходного сигнала, называют обратными коэффициентами.

Уравнения вида B-2a, B-2b, B-3a или B-3b, которые описывают работу фильтра, называются разностными уравнениями.

Достоинства и недостатки КИХ и БИХ фильтров

Преимуществом БИХ фильтров по сравнению с КИХ фильтрами является то, что обычно при выполнении одних и тех же операций для БИХ фильтров требуется меньшее количество коэффициентов. Следовательно, БИХ фильтры работают намного быстрее и не требуют дополнительной памяти, поскольку они используют промежуточные результаты.

Недостатком БИХ фильтров является нелинейность ФЧХ. БИХ фильтры вам подойдут, если в приложении не требуются данные о фазе, например, при простом контроле сигнала. В приложениях, где требуется линейная ФЧХ, следует использовать КИХ фильтры. Вследствие рекурсивного характера БИХ фильтры трудно проектировать и реализовывать.

M. Фильтры с бесконечной импульсной характеристикой

БИХ фильтры – это цифровые фильтры, выходной сигнал которых вычисляется как взвешенная сумма прошлых и текущего значения входной величины. С учетом обозначений отсчетов входной величины x[.] и выходной вtличины y[.], в общем случае разностное уравнение, описывающее БИХ фильтр, имеет вид:

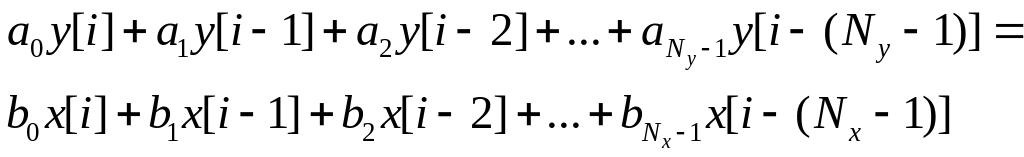
, (B-4)

где N_x – количество прямых коэффициентов (b[k]), N_y – количество обратных коэффициентов (a[j]). Текущий отсчет выходного сигнала под номером i является суммой масштабированного текущего и предыдущих отсчетов входного сигнала (соответственно x[i] и x[i–k] при j  0) и масштабированных предыдущих отсчетов выходного сигнала (y[i–j]). Обычно число N_x равно N_y, и его называют порядком фильтра.

Примечание: Во всех БИХ фильтрах, реализованных в LabVIEW, коэффициент a0 равен 1.

Реальные БИХ фильтры

Благодаря понижению порядка уменьшается количество арифметических операций и, следовательно, становится меньшей погрешность вычислений. Проблема фильтрации высокого порядка заключается в том, что вы быстро сталкиваетесь со случайными погрешностями для порядков более 20–30. Главным образом по этой причине предпочтение отдается каскадным структурам, а не прямым. За более подробной информацией по реализации каскадных структур обратитесь к справке LabVIEW Help. Разумно выбирать порядок в диапазоне от 1 до 20, верхний предел – 30. Более высокий порядок фильтра означает большее количество коэффициентов и более длительное время вычислений.

Импульсная характеристика фильтра, описываемого уравнением B-4, имеет бесконечную длину для ненулевых коэффициентов. Однако в практических приложениях импульсная характеристика устойчивых БИХ фильтров спадает до нуля для конечного количества отсчетов.

На практике частотная характеристика фильтров отличается от характеристики идеального фильтра. В зависимости от формы частотной характеристики среди БИХ фильтров можно выделить следующие виды:

• Фильтры Баттерворта

• Фильтры Чебышева

• Фильтры Чебышева II рода (инверсные фильтры Чебышева)

• Эллиптические фильтры

• Фильтры Бесселя

Далее рассматривается отклик каждого из этих фильтров на входное импульсное воздействие. Сигнал фильтруется с помощью Express VI Filter, а частотная характеристика вычисляется с помощью Frequency Response Function (Mag-Phase) VI без применения окон.

Фильтры Баттерворта

У фильтра Баттерворта нет пульсаций в полосе пропускания или в полосе заграждения. С учетом этого, его называют фильтром с максимально плоской АЧХ, которая является гладкой на всех частотах. На рис. B-29 приведен частотный отклик ФНЧ Баттерворта различных порядков.

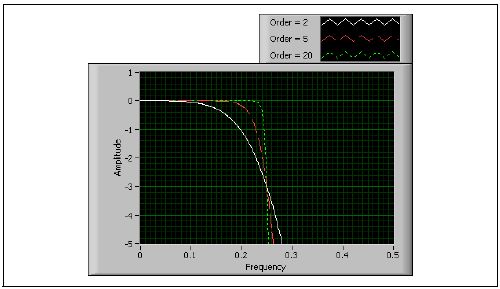
Рисунок B-29. АЧХ фильтра Баттерворта.

Область, где АЧХ фильтра равна 0 дБ или почти равна 0 дБ, называют полосой пропускания. Область, где АЧХ резко приближается к отрицательным значениям (дБ), называют полосой заграждения. Область между полосой пропускания и полосой заграждения, где АЧХ плавно изменяется от 0 в сторону отрицательных значений, называют переходной областью.

Преимуществом фильтров Баттерворта является гладкая, монотонно убывающая АЧХ в переходной области. Как видно на рис. B-29, чем выше порядок фильтра, тем круче переходная область.

Фильтры Чебышева

АЧХ фильтров Баттерворта не всегда точно аппроксимирует АЧХ идеального фильтра из-за медленного спада между полосой пропускания (полезная часть спектра) и полосой заграждения (нежелательная часть спектра). У фильтров Чебышева более узкая переходная область, чем у фильтра Баттерворта того же порядка. Однако это достигается за счет неравномерностей в полосе пропускания. В LabVIEW для фильтра Чебышева вы можете задать максимальное значение этой неравномерности (дБ). АЧХ фильтров Чебышева имеют в полосе пропускания равные по величине пульсации, монотонно убывающую характеристику в полосе заграждения, и более крутой спад в переходной области по сравнению с фильтром Баттерворта того же порядка.

На рис. B-30 приведен отклик ФНЧ Чебышева различных порядков, причем масштаб по оси y выражен в децибелах. С увеличением порядка повышается крутизна переходной области, а также растет количество пульсаций в полосе пропускания.

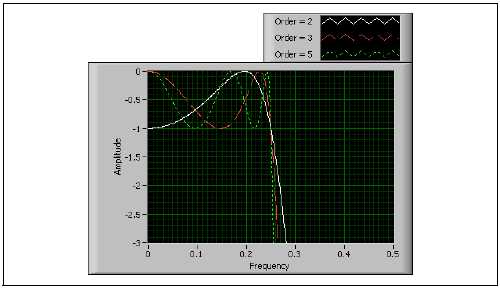
Рисунок B-30. АЧХ фильтра Чебышева

Преимуществом фильтров Чебышева по сравнению с фильтрами Баттерворта является более крутая переходная область между полосой пропускания и полосой заграждения у фильтров низкого порядка, за счет чего обеспечиваются меньшие абсолютные погрешности и более высокие скорости вычислений.

Фильтры Чебышева II рода или инверсные фильтры Чебышева

Фильтры Чебышева II рода, известные как инверсные фильтры Чебышева, похожи по своим свойствам на обычные фильтры Чебышева за исключением того, что в АЧХ фильтров II рода неравномерности – в полосе заграждения, а полоса пропускания максимально плоскоя. Для фильтров Чебышева II рода вы можете задать уровень ослабления (дБ) в полосе заграждения. У АЧХ фильтров II рода пульсации равной амплитуды в полосе заграждения, монотонно убывающая характеристика в полосе пропускания, причем их спад более крутой, чем у фильтров Баттерворта того же порядка. На рис. B-31 приведена АЧХ ФНЧ Чебышева II рода различных порядков.

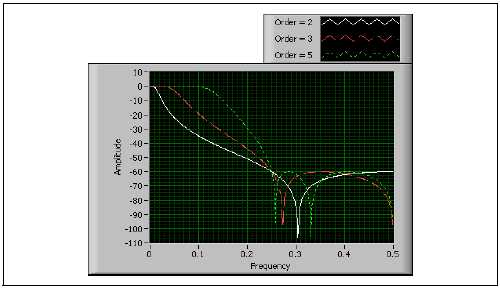
Рисунок B-31. АЧХ фильтра Чебышева II рода

Преимуществом фильтров Чебышева II рода по сравнению с фильтрами Баттерворта является более крутой перепад между полосой пропускания и полосой заграждения, при более низких порядках фильтров. Это обеспечивает меньшую абсолютную погрешность и более высокую скорость вычислений. Преимущество фильтров Чебышева II рода по сравнению с обычными фильтрами Чебышева заключается в том, что у них неравномерность в полосе заграждения, а не в полосе пропускания.

Эллиптические фильтры

Фильтры Чебышева I и II родов имеют более крутую переходную область по сравнению с фильтрами Баттерворта того же порядка, поскольку у них допускаются неравномерности в полосе пропускания (I род) или в полосе заграждения (II род). У эллиптических фильтров неравномерности распределены по полосе пропускания и по полосе заграждения. Для АЧХ таких фильтров характерны одинаковые неравномерности в полосе пропускания и в полосе заграждения. По сравнению с фильтрами Баттерворта или Чебышева того же порядка эллиптическая структура обеспечивает самый крутой перепад между полосой пропускания и полосой заграждения. Этим обусловлена их большая популярность в приложениях, в которых требуются узкие переходные области и допускаются неравномерности. На рис. B-32 приведена АЧХ эллиптического ФНЧ различных порядков.

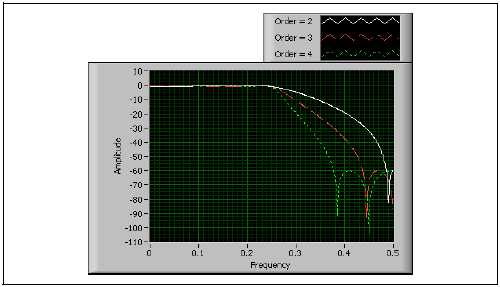
Рисунок B-32. АЧХ эллиптического фильтра

Обратите внимание на то, что крутой перепад АЧХ имеет место для эллиптических фильтров малого четного порядка. Для таких фильтров вы можете задать уровень пульсаций (в дБ) в полосе пропускания и ослабление (в дБ) в полосе заграждения.

Фильтры Бесселя

Фильтр Бесселя проектируют специально для прямоугольных входных воздействий, и поэтому он идеально подходит для цифровой фильтрации. Во многом, как и фильтр Баттерворта, фильтр Бесселя имеет гладкую АЧХ в полосе пропускания и в полосе заграждения. Подавление в полосе заграждения у фильтра Бесселя значительно меньше, чем у фильтра Баттерворта, если оба фильтра одного и того же порядка. Среди всех типов фильтров одинакового порядка фильтр Бесселя имеет самую широкую переходную область. Главным преимуществом этого фильтра является почти линейная ФЧХ в полосе пропускания.

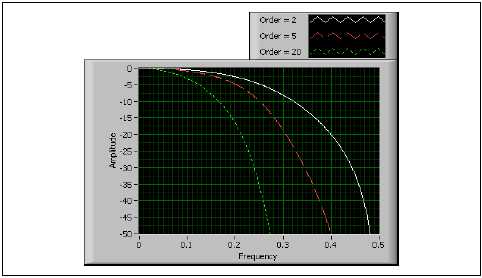
Рисунок B-33. АЧХ фильтра Бесселя

N. Сравнение БИХ фильтров

Рис. B-34 дает возможность сравнить отклик в низкочастотной области пяти различных типов БИХ фильтров одного и того же (пятого) порядка. АЧХ эллиптического фильтра имеет самую узкую переходную область, а АЧХ фильтра Бесселя – самую широкую.

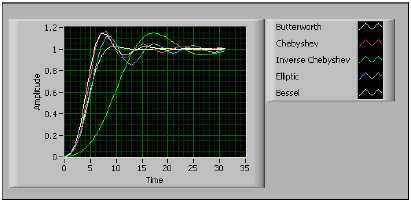
Рисунок B-34. Сравнение БИХ фильтров

В таблице B-7 приводится сравнение фильтров.

Таблица B-7. Сравнение БИХ фильтров

Тип БИХ фильтра	Особенности характеристик	Ширина переходной области для одного и того же порядка	Порядок, требуемый для заданных спецификаций фильтра
Баттерворта (Butterworth)	Нет неравномерностей		
Чебышева (Chebyshev)	Неравномерность в полосе пропускания		
Инверсный Чебышева (Inv. Chebyshev)	Неравномерность в полосе заграждения		
Эллиптический (Elliptic)	Неравномерности и в полосе пропускания, и в полосе заграждения	Самая узкая	Самый низкий
Бесселя (Bessel)	Нет неравномерностей	Самая широкая	Самый высокий

VI, реализующие цифровые фильтры в LabVIEW, справляются со всеми трудностями проектирования, вычислением, распределением памяти, промежуточными преобразованиями данных, они понятны пользователю. Чтобы обработать данные, вам не нужно быть экспертом в области цифровых фильтров или их теории. Вам нужно только задать значения элементов управления, такие как порядок фильтра, частоты среза, уровень неравномерности и ослабление в полосе заграждения.

Принятие решения, какой применять фильтр

Теперь после того как вы познакомились с различными типами фильтров и их характеристиками, возникает вопрос, а какой тип фильтра лучше всего подходит для вашего приложения. На выбор фильтра влияют требование линейности ФЧХ, допустимая неравномерность АЧХ, необходимость узкой переходной области. Блок-схема на рис. B-35 поясняет, как правильно выбирать фильтр. Возможно, вам потребуется поэкспериментировать с несколькими различными вариантами, прежде чем подберете наилучший из них.

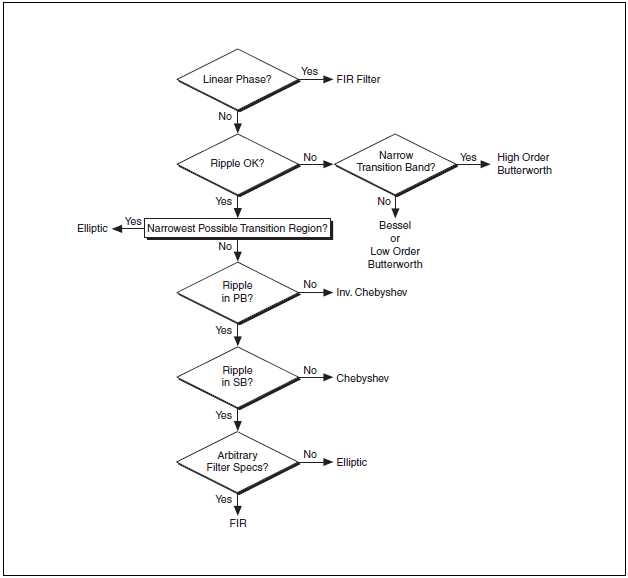
Рисунок B-35. Блок-схема выбора фильтра

Linear Phase? – ФЧХ линейная?; Ripple OK? – Неравномерность в норме?; Narrowest Possible Transition Region? – Переходная область достаточно узкая?; Ripple in PB? – Неравномерность в полосе пропускания?; Ripple in SB? – Неравномерность в полосе заграждения?; Arbitrary Filter Specs? – Спецификации фильтра произвольные? Narrow Transition Band? – Переходная область узкая?; FIR Filter – КИХ фильтр, High Order – высокого порядка, Low Order – низкого порядка.

O. Переходная характеристика БИХ фильтров

Сигнал на выходе обобщенного БИХ фильтра записывается в соответствии с формулой:

(B-5)

где N_x – количество прямых коэффициентов, N_y – количество обратных коэффициентов, a₀ принят равным 1. Для фильтра второго порядка, у которого N_x = N_y = 2, соответствующее разностное уравнение имеет вид:

(B-6)

Чтобы вычислить значение текущего отсчета (в i-й момент времени) сигнала на выходе фильтра, вам нужно знать два предыдущих отсчета выходного сигнала (в (i–1)-й и (i–2)-й момент времени) и текущий отсчет входного сигнала (в i-й момент времени), а также два предыдущих отсчета входного сигнала (в (i–1)-й (i–2)-й моменты времени).

Предположим, что вы начали процесс фильтрации с первого отсчета входных данных. В этот момент времени у вас нет предыдущих отсчетов входного (x[i–1] и x[i–2]) или выходного (y[i–1] и y[i–2]) сигнала. По умолчанию эти величины полагают равными нулю. Когда вы получаете второй отсчет данных, у вас уже есть предыдущий отсчет входного (x[i–1]) и выходного (y[i–1]) сигналов, но нет отсчетов x[i–2] и y[i–2], которые снова по умолчанию принимаются равными нулю. После начала обработки третьего отсчета входных данных, всем членам правой части уравнения B-6 присвоены ранее вычисленные значения. Имеет место некоторая задержка, по истечении которой ранее вычисленные значения присваиваются всем членам правой части описывающего фильтр разностного уравнения. Выходной сигнал фильтра в течение этого временного интервала называют переходной характеристикой. Для ФНЧ и ФВЧ длительность переходного процесса, или задержка, равна порядку фильтра. У ПФ и ЗФ эта задержка в 2 раза больше.

БИХ фильтры обладают следующими особенностями.

• Отсчеты с отрицательными индексами, которые получаются из уравнения B-4, при первом вызове VI принимаются равными нулю.

• Поскольку мы предполагаем, что начальное состояние фильтра равно нулю (отсчеты с отрицательными индексами), появляется переходный процесс пропорциональный порядку фильтра, перед тем как фильтр достигнет установившегося режима. Продолжительность переходной характеристики или задержка для ФНЧ и ФВЧ равна порядку фильтра.

• Продолжительность переходной характеристики в ЗФ и РФ в два раза превышает порядок фильтра.

При каждом вызове Filter VI на выходе появляется переходный процесс (рис. B-36), который вы можете удалить с помощью нескольких подряд вызовов VI при включенной памяти состояний VI. Для этого необходимо присвоить параметру init/cont значение TRUE (включить режим непрерывной фильтрации).

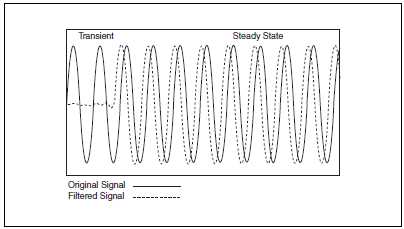
Рисунок B-36. Сигнал после фильтрации

• Количество элементов выходной отфильтрованной последовательности равно количеству элементов входной последовательности.

• Фильтр хранит значения внутренних переменных состояния по окончании фильтрации.

P. Фильтры с конечной импульсной характеристикой

В связи с тем, что текущее значение выходного сигнала БИХ фильтра зависит от его предыдущих значений, а также текущего и предыдущих значений входного сигнала, такой фильтр обладает памятью бесконечного размера, и, следовательно, импульсной характеристикой бесконечной длины.

У цифровых фильтров с конечной импульсной характеристикой (КИХ фильтров) импульсная характеристика имеет конечную длину. КИХ фильтры также называют нерекурсивными фильтрами, сверточными фильтрами или фильтрами скользящего среднего, поскольку выходной сигнал такого фильтра записывается с помощью свертки конечной длины:

,

где x – входная последовательность отсчетов, у – выходная отфильтрованная последовательность отсчетов, h – коэффициенты КИХ фильтра.

Текущий отсчет выходного сигнала КИХ фильтра зависит только от текущего и предыдущих отсчетов входного сигнала. А т.к. текущее значение выходного сигнала не зависит от его предыдущих значений, импульсная характеристика КИХ фильтра спадает до нуля в течение конечного интервала времени. Выходной сигнал обобщенного КИХ фильтра описывается формулой:

(B-5)

где M – количество звеньев фильтра, b₀, b₁, …, b_M–1 – коэффициенты фильтра.

КИХ фильтры обладают некоторыми важными свойствами:

• Для них можно добиться линейности ФЧХ, чтобы пропускать через них сигнал без фазовых искажений.

• Они всегда устойчивы. В процессе проектирования или разработки таких фильтров нет необходимости задумываться над вопросами устойчивости.

• КИХ фильтры имеют более простую структуру, и их легче реализовывать, чем БИХ фильтры.

• На рис. B-37 приведены типовые АЧХ и ФЧХ КИХ фильтров для нормированных частот. На ФЧХ возникают точки разрыва вследствие появления точек разрыва на АЧХ, вычисляемой с использованием абсолютных значений. Разрывы ФЧХ соответствуют значениям фазы, кратным . Однако ФЧХ полностью линейна.

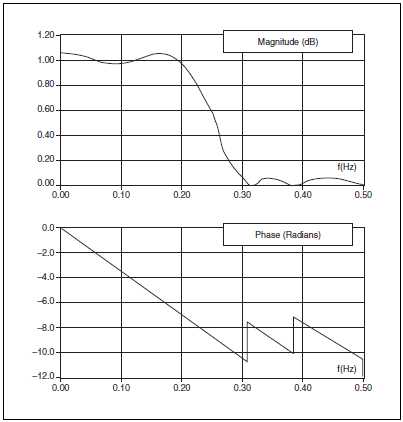
Рисунок B-37. Типовая АЧХ (дБ – вверху) и ФЧХ (рад – внизу) КИХ фильтров

Простейшим методом проектирования КИХ фильтров с линейной ФЧХ является метод с применением окон. При использовании такого метода следует начинать с построения идеальной частотной характеристики и вычисления соответствующей импульсной характеристики. Затем нужно обрезать полученную импульсную характеристику, чтобы получить конечное количество коэффициентов. Такое обрезание импульсной характеристики порождает так называемый эффект Гиббса – колебательный характер АЧХ возле резких перепадов (частот среза).

Вы можете уменьшить влияние эффекта Гиббса путем применения к импульсной характеристике сглаживающих окон. Уменьшение значений коэффициентов КИХ фильтра с каждой стороны позволяет уменьшить высоту боковых лепестков АЧХ. Недостаток этого метода заключается в том, что расширяется основной лепесток, а это приводит к расширению переходной области возле частот среза.

Выбор оконной функции похож на выбор между БИХ фильтрами Баттерворта и Чебышева тем, что ищется компромисс между шириной боковых лепестков возле частот среза и шириной переходной области.

Выводы

• Быстрое вычисление дискретного преобразования Фурье (ДПФ) возможно за счет использования алгоритма, называемого быстрым преобразованием Фурье (БПФ). БПФ можно применять тогда, когда количество отсчетов сигнала равно степени двойки.

• С помощью ДПФ/БПФ можно вычислить спектр мощности путем возведения в квадрат амплитуд отдельных спектральных составляющих. Эту функцию автоматически выполняет VI Power Spectrum в составе библиотеки расширенного спектрального анализа. Спектр на выходе данного VI формируется в единицах квадрата среднеквадратического напряжения ( ). Спектр мощности не дает никакой информации о фазе.

• ДПФ, БПФ и спектр мощности полезны для спектрального анализа стационарных и нестационарных сигналов. В результате БПФ получается усредненный спектральный состав за все время наблюдения сигнала. Наиболее предпочтительно использовать БПФ для анализа стационарных сигналов, когда спектральный состав незначительно меняется во времени в процессе измерения или когда вы хотите вычислить среднюю энергию по каждой гармонике.

• Чтобы уменьшить растекание спектра, конечный во времени сигнал умножается на оконную функцию.

• С помощью окон можно разделить два гармонических сигнала, у которых сильно различаются амплитуды, но очень близкие частоты.

• У реальных фильтров коэффициент передачи в полосе пропускания не всегда может быть равен 1, а ослабление в полосе заграждения не всегда может быть равно –. Между этими полосами существует некоторая переходная область конечной ширины.

• Ширина переходной области зависит от порядка фильтра, и она уменьшается при увеличении порядка.

• Сигнал на выходе КИХ фильтров зависит только от текущего и предыдущих отсчетов входного сигнала, а выходной сигнал БИХ фильтров зависит от текущего и предыдущего отсчетов входного сигнала, и, кроме того, еще от предыдущих отсчетов выходного сигнала.

• БИХ фильтры можно классифицировать в зависимости от наличия неравномерностей в полосе пропускания и/или в полосе заграждения.

• Т.к. текущий отсчет выходного сигнала зависит от его предыдущих отсчетов, то при каждом вызове VI на выходе БИХ фильтра возникает перепад, который можно устранить после первого вызова, присвоив элементу управления init/cont значение TRUE.

• Конфигурирование спектральных вычислений и параметров фильтрации для некоторого заданного входного сигнала облегчают Spectral Measurements Express VI и Filter Express VI.

Заметки

С

Приложение С Дополнительная информация и ресурсы

В этом приложении содержится дополнительная информация о технической поддержке National Instruments и ресурсах LabVIEW.

Техническая поддержка National Instruments

Обратитесь к следующим разделам отмеченного наградами веб-сайта National Instruments ni.com для получения технической поддержки и профессиональных услуг:

• Support (Поддержка) – техническая поддержка по адресу ni.com/support включают следующие разделы:

• Self-Help Technical Resources (Технические ресурсы для самостоятельного решения проблем) – обратитесь за ответами и решениями на сайт ni.com/support, где находятся программные драйвера и обновления, База знаний с возможностью поиска, руководства по продукции NI, мастера по пошаговому поиску и устранению неисправностей, тысячи образцов программ, учебных пособий, драйверов измерительных приборов и т.д. Зарегистрированные пользователи получают также доступ к дискуссионным форумам NI по адресу ni.com/forums. Специалисты по применению NI гарантируют ответ в режиме он-лайн на каждый заданный вопрос.

• Standard Service Program Membership (Членство в стандартной программе обслуживания) – эта программа позволяет ее участникам непосредственно обращаться к специалистам по применению NI в режиме «тет-а-тет» по телефону и электронной почте для получения технической поддержки, а также обеспечивает эксклюзивный доступ по требованию к учебным модулям через Services Resource Center (Услуги ресурсного центра). NI предлагает дополнительное членство в течение года после покупки, затем вы можете его продлить.

Для получения информации о других возможностях технической поддержки в вашем регионе, посетите сайт ni.com/services или обратитесь в местный офис по ni.com/contact.

• System Integration (Системная интеграция) – если вы столкнулись с ограничениями по времени, техническим ресурсам и иными сложностями при работе над проектом, члены National Instruments Alliance Partner (Альянс партнеров NI) могут вам помочь. NI Alliance Partner объединяет системных интеграторов, консультантов и поставщиков технических средств, которые проводят экспертизу и предоставляют пользователям всестороннюю помощь. Программа NI Alliance Partner гарантирует квалифицированную помощь специалистов при разработке систем и приложений. Для получения дополнительной информации свяжитесь с местным офисом NI или посетите сайт ni.com/alliance.

Если вы провели поиск по сайту ni.com и не нашли ответа на свои вопросы, обратитесь в ваш местный офис или в центральный офис NI. Номера телефонов наших офисов во всем мире можно найти в начале данного руководства. Вы можете также посетить раздел Worldwide Offices на сайте ni.com/niglobal для доступа к веб-сайтам филиалов, где имеется обновляемая контактная информация, телефоны службы поддержки, адреса электронной почты и информация о текущих событиях.

Другие учебные курсы National Instruments

National Instruments предлагает несколько учебных курсов для пользователей LabVIEW. Эти курсы продолжают обучение, начатое вами в настоящем курсе и продвигают знания на новый уровень. Посетите сайт ni.com/training для приобретения материалов курса или записи на практические курсы с инструктором, проводимые по всему миру.

Сертификация National Instruments

Сертификат NI подтверждает вашу квалификацию в работе с продукцией и технологиями NI. Предприятия средств автоматизации и измерений, ваши работодатели, клиенты и коллеги распознают ваш сертификат NI, как признак знаний и навыков, которые вы получили на практике. Посетите сайт ni.com/training для получения дополнительной информации о программе сертификации NI.

Ресурсы LabVIEW

Ниже описано, как вы можете получить дополнительную информацию о LabVIEW.

Публикации о LabVIEW

О программировании и применении LabVIEW написано много книг. Веб-сайт National Instruments содержит список всех книг о LabVIEW с ссылками на места, где их можно приобрести. Также приведена информация об издателях, чтобы вы могли напрямую связаться с издательством для получения дополнительной информации о содержании и порядке приобретения книг по LabVIEW и родственных книг о компьютерных измерениях и автоматизации.

Web-сайты

ni.com/products

ni.com/labview

ni.com/dataacquisition

ni.com/sensors

ni.com/signalconditioning

Заметки