I. Идеальные фильтры

Фильтры изменяют уровень нежелательных гармоник или подавляют их вовсе. В зависимости от частотного диапазона, в котором фильтры пропускают или ослабляют спектральные составляющие, их можно разделить на четыре типа:

• Фильтр нижних частот (ФНЧ - Lowpass) – пропускает нижние частоты, но ослабляет верхние частоты

• Фильтр верхних частот (ФВЧ -Highpass)– пропускает верхние частоты, но ослабляет нижние частоты

• Полосовой фильтр(ПФ - Bandpass) – пропускает определенную полосу частот.

• Заграждающий (режекторный) фильтр (ЗФ - Bandstop) – ослабляет определенную полосу частот.

На рис. B-23 приведена идеальная АЧХ для всех четырех типов фильтров (слева направо).

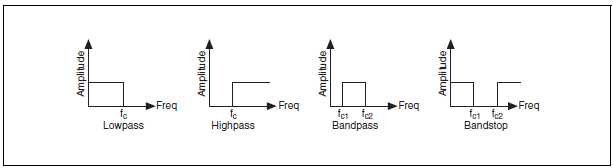
Рисунок B-23. АЧХ идеальных фильтров

ФНЧ пропускает все частоты ниже f_c, а ФВЧ – все частоты выше f_c. ПФ пропускает все частоты между f_c1 и f_c2, а ЗФ – ослабляет все частоты между f_c1 и f_c2. Значения частоты f_c, f _c1, f _c2 называют частотами среза, которые необходимо задавать при проектировании фильтров.

Диапазон частот, пропускаемых фильтром, называют полосой пропускания фильтра. Идеальный фильтр в полосе пропускания имеет единичный коэффициент передачи (0 дБ), так что амплитуда выходного сигнала не усиливается, но и не ослабляется. Полоса заграждения соответствует диапазону частот, которые совсем не пропускаются фильтром или ослабляются. На рис. B-24 приведены полосы пропускания (PB) и заграждения (SB) для различных типов фильтров.

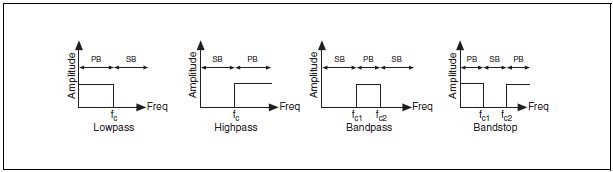
Рисунок B-24. Полосы пропускания и заграждения фильтров

ФНЧ и ФВЧ имеют одну полосу пропускания и одну полосу заграждения, ПФ имеет одну полосу пропускания и две полосы заграждения, ЗФ имеет две полосы пропускания и одну полосу заграждения.

Влияние фильтров на спектральный состав сигнала

Сигнал, который состоит из гармоник на частотах 10 Гц, 30 Гц и 50 Гц, пропускается через ФНЧ, ФВЧ, ПФ и ЗФ. У ФНЧ и ФВЧ частота среза равна 20 Гц, а у ПФ и ЗФ частоты среза равны 20 Гц и 40 Гц. На рис. B-25 показан спектр сигнала на выходе фильтра для каждого случая.

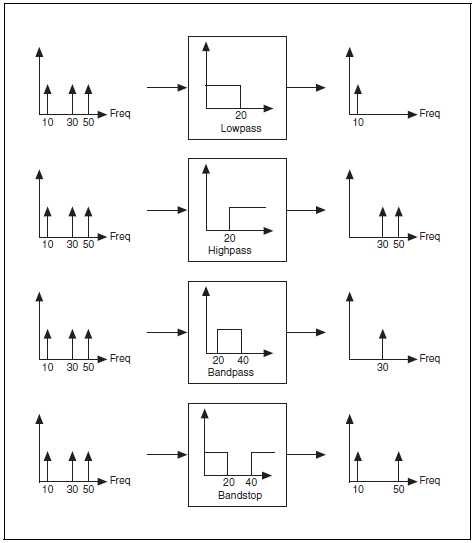
Рисунок B-25. Спектры сигналов на выходе фильтров

J. Реальные (неидеальные) фильтры

Переходная полоса фильтра

Идеальный фильтр должен иметь единичный коэффициент передачи (0 дБ) в полосе пропускания и нулевой коэффициент передачи (– дБ) в полосе заграждения. Однако, при практической реализации фильтра не все из этих критериев могут быть удовлетворены. На самом деле всегда существует некоторая переходная область конечной ширины между полосой пропускания и полосой заграждения, в которой коэффициент передачи фильтра постепенно меняется от единицы (0 дБ) в полосе пропускания до нуля (– дБ) в полосе заграждения. На рис. B-26 приведены полоса пропускания (PB), полоса заграждения (SB), переходная область (TR) для различных типов неидеальных фильтров, у которых полосой пропускания становится частотный диапазон, где коэффициент передачи фильтра изменяется от 0 дБ до –3 дБ. Несмотря на то, что самым распространенным является диапазон –3 дБ, в зависимости от приложения могут быть также использованы другие значения (–0.5 дБ, –1 дБ и т.д.).

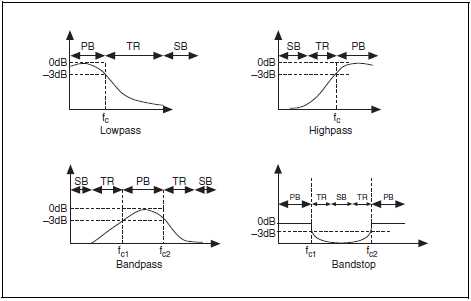
Рисунок B-26. Переходные полосы фильтров

Неравномерность в полосе пропускания и ослабление в полосе заграждения

Во многих приложениях допускается, чтобы коэффициент передачи фильтра в полосе пропускания немного отклонялся от единицы. Такое отклонение называют неравномерностью в полосе пропускания, которая представляет собой разность между действительным коэффициентом передачи и желаемым коэффициентом передачи, равным единице. Поскольку ослабление в полосе заграждения не может быть бесконечным, вам следует задать его желаемое значение. И неравномерность в полосе пропускания (Ripple – пульсации), и ослабление в полосе заграждения измеряются в децибелах (дБ):

дБ = 20 × log₁₀ (A_o(f)/ A_i(f)),

где log₁₀ означает логарифм по основанию 10, A_i(f) и A_o(f) – амплитуды отдельной гармоники на частоте f до и после фильтрации.

Например, для неравномерности –0.02 дБ на основании данной формулы имеем:

– 0.02 = 20 × log₁₀ (A_o(f)/ A_i(f)),

A_o(f)/ A_i(f) = 10^–0.001 = 0.9977,

откуда следует, что отношение амплитуды выходного сигнала к амплитуде входного сигнала близко к единице.

Если ослабление в полосе заграждения равно –60 дБ, то

– 0.60 = 20 × log₁₀ (A_o(f)/ A_i(f)),

A_o(f)/ A_i(f) = 10^–3 = 0.001,

откуда следует, что амплитуда выходного сигнала в 1000 раз меньше амплитуды входного сигнала. Понятия неравномерности в полосе пропускания и ослабления в полосе заграждения без соблюдения масштаба поясняются на рис. B-27.

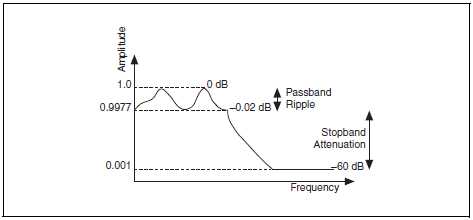
Рисунок B-27. Неравномерность в полосе пропускания

Примечание: Обычно ослабление записывают в децибелах без знака «минус», хотя, как правило, он в данном случае подразумевается.

K. Преимущества цифровых фильтров по сравнению с аналоговыми фильтрами

И на входе, и на выходе аналогового фильтра – аналоговый сигнал. И входная величина x(t), и выходная величина y(t) являются функциями непрерывной переменной t и могут принимать бесконечное множество значений. Аналоговые фильтры начали проектировать раньше цифровых примерно на 50 лет. Во многих книгах по проектированию аналоговых фильтров описываются простые, легко проверяемые схемы фильтров. Однако суть аналоговых фильтров часто скрыта от специалистов, поскольку требует продвинутых математических знаний и понимания процессов, происходящих в системе, на которые влияет фильтр.

Современные средства дискретизации и цифровой обработки сигналов делают возможной замену аналоговых фильтров на цифровые в приложениях, где требуется гибкость и возможность программирования. К таким приложениям относятся аудиотехника, телекоммуникации, геофизика и медицинский мониторинг. Ниже поясняются преимущества цифровых фильтров:

• Они являются программируемыми и, следовательно, их легко построить и протестировать.

• Их легче реализовать, поскольку для этого требуются только арифметические операции умножения и сложения/вычитания.

• Они стабильны (их параметры не меняются в зависимости от времени или температуры), и их поведение предсказуемо.

• Им не присущ дрейф в зависимости от температуры или влажности, а также не требуются прецизионные компоненты.

• Они обладают наилучшим соотношением «быстродействие-цена».

• Для них не существенна изменчивость производственного процесса или старение.

L. БИХ и КИХ фильтры

Еще одним классификационным признаком для фильтров является их импульсная характеристика – реакция фильтра на единичный импульс x[0] = 1, x[i] = 0 при i  0 (рис. B-28). Преобразование Фурье от импульсной характеристики называют частотной характеристикой фильтра, из которой следует, каким будет сигнал на выходе и каким будет коэффициент передачи на различных частотах. У идеального фильтра коэффициент передачи должен быть равным 1 в полосе пропускания и равным 0 в полосе заграждения. В полосе пропускания все спектральные составляющие передаются на выход без изменений, а полосе заграждения на выход ничего не передается.

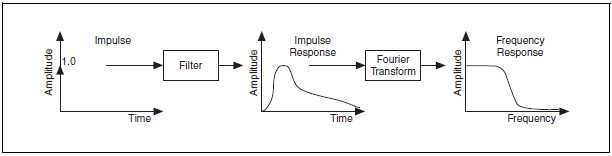
Рисунок B-28. Импульсная характеристика фильтра