Интегрирующий (двойного интегрирования)

Этот метод аналого-цифрового преобразования основан на интегрировании аналогового сигнала. У этого типа АЦП есть несколько преимуществ - высокое разрешение, хорошая линейность и подавление входных помех при помощи усреднения. Главный его недостаток – большое время преобразования. Поэтому интегрирующие АЦП обычно используются в цифровых мультиметрах и прочих измерительных устройствах, не требующих высокой скорости.

Дельта-Сигма модуляция

Самая передовая технология АЦП – дельта-сигма АЦП. В этих АЦП используются дельта-сигма модуляторы, а также дискретизация с запасом по частоте и цифровыми фильтрами для обеспечения высоких частот дискретизации, высокого разрешения и лучшей из всех типов АЦП линейности. Например, этот тип АЦП обладает 16-разрядным разрешением на частоте 48х10³ Отсчетов/с без дифференциальной нелинейности.

Таблица A-2. Преимущества/использование различных типов АЦП

Типы АЦП	Преимущества/Использование
С последовательным приближением	Высокое разрешение Высокая скорость Легко мультиплексировать Часто используется в платах DAQ Сигналы постоянного тока
Параллельный	Самая высокая скорость Отработанная технология Более дорогой
Интегрирующий	Высокое разрешение Хорошее подавление помех Хорошая линейность Отработанная технология Большое время преобразования Обычно используется в цифровых мультиметрах
Дельта-сигма	Высокое разрешение Отличная линейность Встроенная защита от искажения спектра Сигналы переменного тока

Заметки

В

Приложение В. Обработка сигналов

В этой лекции излагаются основы обработки сигналов.

Темы

1. Дискретное преобразование Фурье (ДПФ) и быстрое преобразование Фурье (БПФ)

2. Информация об амплитуде и фазе

3. Разрешение по частоте и симметрия ДПФ/БПФ

4. Спектр мощности

5. Утечки спектра и сглаживающие окна

6. Характеристики различных типов оконных функций

7. Выбор типа окна, который необходимо использовать

8. Фильтрация

9. Идеальные фильтры

10. Реальные фильтры

11. Преимущество цифровых фильтров по сравнению с аналоговыми фильтрами

12. БИХ и КИХ фильтры

13. Фильтры с бесконечной импульсной характеристикой

14. Сравнение БИХ фильтров

15. Переходная характеристика БИХ фильтров

16. Фильтры с конечной импульсной характеристикой

A. Дискретное преобразование Фурье (ДПФ) и быстрое преобразование Фурье (БПФ)

Отсчеты сигнала, полученные с устройства ввода-вывода, являются представлением этого сигнала во временной области. Такое представление дает амплитуды сигнала в моменты его выборки. Во многих случаях вам в первую очередь может потребоваться частотный состав сигнала, а не амплитуды отдельных отсчетов. Как известно, описание сигнала в виде отдельных частотных составляющих называют представлением сигнала в частотной области. Данное представление позволяет более глубоко проанализировать сигнал и систему, которая его сформировала.

Алгоритм, используемый для преобразования отсчетов из временной области в частотную область, известен под названием «дискретное преобразование Фурье (ДПФ)». Такое преобразование устанавливает соответствие между отсчетами сигнала во временной области и их представлением в частотной области (рис. B-1). ДПФ применяют в таких областях как спектральный анализ, прикладная механика, акустика, рентгенография, численный анализ, измерительная техника и телекоммуникации.

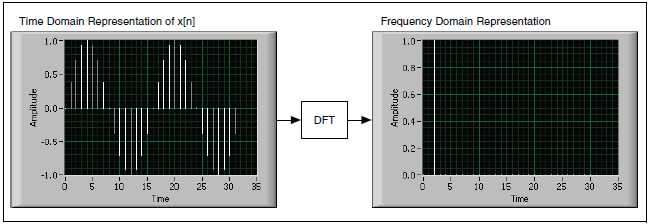
Рисунок B-1. Дискретное преобразование Фурье

Time Domain Representation of x[n] – представление сигнала x[n] во временной области, Frequency Domain Representation – представление сигнала в частотной области

Если вы получаете с устройства ввода-вывода N отсчетов во временной области и применяете к ним ДПФ, то результатом являются также N отсчетов, но уже в частотной области.

Если сигнал подвергнуть дискретизации с некоторой частотой f_s, то этой частоте соответствует интервал дискретизации t:

Дискретные сигналы обозначают как x[i], 0iN – 1 (таким образом, всего у вас N отсчетов). Если к этим N отсчетам применить дискретное преобразование Фурье, то результирующим представлением сигнала в частотной области будет (X[k], 0kN – 1).

, (B-1)

Обратите внимание на то, что представление сигнала во временной области x и представление сигнала в частотной области X состоят всего из N отсчетов. Аналогично интервалу t между отсчетами x во временной области в частотной области используют интервал f между частотными составляющими X

,

который называют разрешением по частоте. Чтобы улучшить разрешение по частоте (уменьшить f ), следует увеличить количество отсчетов N, оставляя постоянной частоту дискретизации f_s, или уменьшить частоту дискретизации f_s при неизменном количестве отсчетов N.

Быстрое преобразование Фурье (БПФ) – это алгоритм, который применяется для быстрого вычисления ДПФ, когда количество отсчетов (N) равно степени числа 2. По количеству полученных отсчетов LabVIEW определяет, какой алгоритм использовать. Во всех VI LabVIEW применяется набор функций БПФ.

Пример вычисления ДПФ

Обозначим X[0] постоянную составляющую или среднее значение сигнала. Чтобы увидеть результат вычисления ДПФ по уравнению B-1, рассмотрим постоянный во времени сигнал с уровнем +1 В. На рис. B-2 показаны четыре отсчета этого сигнала.

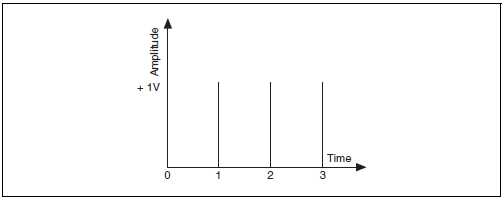
Рисунок B-2. Отсчеты сигнала постоянного тока

Значение каждого из этих отсчетов равно +1, и они образуют временную последовательность

Рассчитав ДПФ этой последовательности по уравнению B-1 и применив формулу Эйлера

получим:

Как и следовало ожидать, все частотные составляющие, кроме постоянной составляющей X[0], равны нулю. Однако, вычисленное значение X[0] зависит от количества отсчетов N. В нашем случае для N=4 X[0] = 4. Если N=10, что в результате вычислений у вас получилось бы X[0]=10. Эта зависимость от N также имеет место для других частотных составляющих X[.]. Обычно для получения правильного значения уровня частотной компоненты результат ДПФ делят на N.

B. Информация об амплитуде и фазе

Вы уже видели, из N отсчетов входного сигнала получается N отсчетов ДПФ. Таким образом, количество отсчетов сигнала во временной и в частотной области одно и тоже. Как следует из уравнения B-1, независимо от того, действительные или комплексные отсчеты входного сигнала x[i], составляющие сигнала в частотной области X[k] всегда комплексные, хотя их мнимая часть может быть равна нулю. Поскольку ДПФ является комплексным, оно состоит из двух частей: амплитуды и фазы. Для реальных сигналов (отсчеты x[i] вещественные), которые поступают с выхода одного из каналов устройства ввода-вывода, ДПФ обладает симметрией относительно отсчета по частоте с номером N/2:

для амплитуды |X[k]| = |X[N–k]|,

для фазы Arg (X[k]) = – Arg (X[N–k])

Как известно, амплитуда X[k] является четной симметричной функцией, а фаза X[k] – нечетной симметричной функцией. Четной называют такую функцию, которая симметрична относительно оси y, а нечетной – функцию, которая симметрична относительно начала координат (рис. B-3).

Рисунок B-3. Четная симметрия (Even) и нечетная симметрия (Odd)

Такая симметрия ведет к дублированию информации, которая содержится в N отсчетах ДПФ. В связи с этим нужно вычислять или отображать только половину отсчетов ДПФ, а вторую половину можно получить за счет симметрии.

Примечание: Если входной сигнал комплексный, ДПФ получается несимметричным, и таким методом пользоваться нельзя.

C. Разрешение по частоте и симметрия ДПФ/БПФ

Если интервал дискретизации составляет t секунд и принято, что первый отсчет (при k = 0) соответствует моменту времени 0 секунд, k-й отсчет (k > 0, k – целое) соответствует моменту времени kt секунд. Аналогично смысл разрешения по частоте заключается в том, что k-я составляющая спектра ДПФ соответствует частоте kf Гц. Это справедливо только для половины отсчетов. Другая половина описывает спектральные составляющие с отрицательными частотами. В зависимости от того, четно или нечетно количество отсчетов N, у вас может по-разному интерпретироваться частота, которая соответствует k-му отсчету ДПФ.

Четное число отсчетов

Предположим, что число отсчетов N четное. Введем обозначение .

В таблице B-1 приведены частоты, которым соответствует каждый элемент комплексной последовательности (массива) X, полученной в результате ДПФ.

Таблица B-1. Соответствие частот элементам массива X

Элемент массива	Частота
X[0]	постоянная составляющая
X[1]	f
X[2]	2f
X[3]	3f
…	…
X[p–2]	(p–2) f
X[p–1]	(p–1) f
X[p]	pf (частота Найквиста)
X[p+1]	–(p–1)f
X[p+2]	–(p–2)f
…	…
X[N–3]	–3f
X[N–2]	–2f
X[N–1]	–1f

p-й элемент X[p] соответствует частоте Найквиста. Отрицательные элементы во втором столбце за пределами частоты Найквиста представляют собой отрицательные частоты.

Например, при N = 8, p = N/2 = 4 имеем:

X[0]	постоянная составляющая
X[1]	f
X[2]	2f
X[3]	3f
X[4]	3f (частота Найквиста)
X[5]	–3f
X[6]	–2f
X[7]	–f

Значение амплитуд компонентов пар X[1] и X[7], X[2] и X[6], X[3] и X[5] одинаково. Различие между ними заключается в том, что X[1], X[2] и X[3] соответствуют положительным частотам, а X[5], X[6] и X[7] – отрицательным частотам. Следует учесть, что составляющей X[4] соответствует частота Найквиста.

Рассматриваемая комплексная последовательность частотных компонентов для N = 8 приведена на рис. B-4.

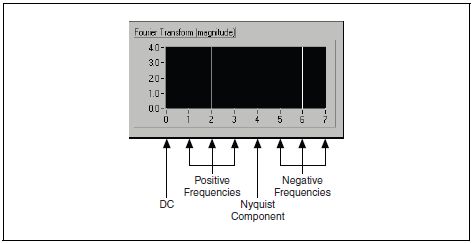
Рисунок B-4. Двустороннее преобразование для N = 8

Такую форму представления спектра, где видны спектральные составляющие и на положительных, и отрицательных частотах, называют двусторонним преобразованием Фурье.

Нечетное число отсчетов

Предположим, что число отсчетов N нечетное. Введем обозначение . В таблице B-2 приведены частоты, которым соответствует каждый элемент комплексной последовательности (массива) X, полученной в результате ДПФ.

Таблица B-2. Соответствие частот элементам массива X

Элемент массива	Частота
X[0]	постоянная составляющая
X[1]	f
X[2]	2f
X[3]	3f
…	…
X[p–1]	(p–1) f
X[p]	pf
X[p+1]	–pf
X[p+2]	–(p–1) f
…	…
X[N–3]	–3f
X[N–2]	–2f
X[N–1]	–f

При нечетном N, значение N/2 является числом дробным. Следовательно, нет компонента, равного частоте Найквиста.

Например, при N = 7, p = (N–1)/2 = (7–1)/2 = 3 имеем:

X[0]	постоянная составляющая
X[1]	f
X[2]	2f
X[3]	3f
X[4]	–3f
X[5]	–2f
X[6]	–f

Значение амплитуд компонентов пар X[1] и X[6], X[2] и X[5], X[3] и X[4] одинаково. Однако X[1], X[2] и X[3] соответствуют положительным частотам, а X[4], X[5] и X[6] – отрицательным частотам. Поскольку N является нечетным числом, на частоте Найквиста нет спектральной составляющей.

Рис. B-5 иллюстрирует приведенную выше таблицу для N = 7.

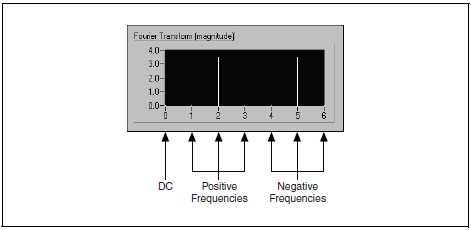
Рисунок B-5. Двустороннее преобразование для N = 7

Это тоже двустороннее преобразование Фурье, поскольку здесь есть спектральные составляющие и на положительных, и на отрицательных частотах.

Быстрые преобразования Фурье

Непосредственное применение ДПФ (уравнение B-1) к N отсчетам требует выполнения примерно N² сложных математических операций, и этот процесс занимает слишком много времени. Однако, если размер последовательности отсчетов является степенью числа 2,

для m = 1, 2, 3, …

вы можете реализовать вычисление ДПФ с помощью примерно N log₂ (N) операций. Это значительно ускоряет процесс выполнения ДПФ. В литературе по сигнальным процессорам (DSP) такие алгоритмы называют быстрыми преобразованиями Фурье (БПФ). БПФ – это быстродействующий алгоритм для вычисления ДПФ при количестве отсчетов (N), равном степени числа 2.

К преимуществам БПФ относятся быстрое выполнение и эффективное использование памяти, поскольку VI в процессе вычислений замещает ранее полученные данные новыми. Размер входной последовательности должен быть равен степени числа 2. Последовательность произвольного размера эффективно может выполнять ДПФ, однако ДПФ работает медленнее, чем БПФ, и использует больший объем памяти, поскольку в процессе его выполнения необходимо хранить промежуточные результаты.

Дополнение последовательности отсчетов нулями

Чтобы размер входной последовательности стал равными степени числа 2, ее дополняют нулями так, чтобы полное количество отсчетов равнялось ближайшей большей степени двойки. Например, имеющиеся у вас 10 отсчетов сигнала можно дополнить шестью нулями (рис. B-6), чтобы итоговое количество отсчетов стало равным 16 (=2⁴).

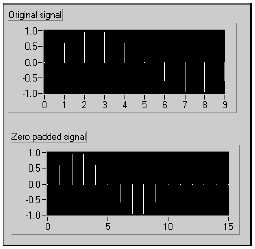
Рисунок B-6. Дополнение последовательности отсчетов нулями

Original signal – исходный сигнал, Zero padded signal – сигнал, дополненный нулями

Помимо повышения быстродействия, дополнение количества отсчетов до степени двойки способствует также улучшению разрешения по частоте за счет увеличения количества отсчетов N (как вы помните, ).

D. Спектр мощности

ДПФ или БПФ реального сигнала является комплексным, т.е. каждая спектральная составляющая имеет действительную и мнимую часть. Мощность каждой составляющей можно получить путем возведения в квадрат ее амплитуды. Поэтому мощность k-й спектральной составляющей (k-го элемента ДПФ/БПФ) записывается как |X[k]|². Как известно, график, на который нанесены мощности каждой спектральной составляющей, называют спектром мощности. В связи с тем, что ДПФ/БПФ реального сигнала обладает симметрией, мощность составляющей на положительной частоте kf равна мощности на соответствующей отрицательной частоте – kf, что не относится к постоянной составляющей и составляющей на частоте Найквиста. Полная мощность постоянной составляющей и составляющей на частоте Найквиста соответственно записываются как |X[0]² и |X[N/2]².

Потеря информации о фазе

Из-за того, что мощность получается путем возведения в квадрат амплитуды ДПФ/БПФ, спектр мощности всегда получается вещественным, и вся информация о фазе теряется. Чтобы получить информацию о фазе, следует применять ДПФ/БПФ, которое дает результат в комплексной форме.

Спектр мощности годится для приложений, в которых информация о фазе не требуется, например, для вычисления мощности гармонических составляющих сигнала. Вы можете подать синусоидальный сигнал на вход нелинейной системы и пронаблюдать мощность гармоник на выходе.

Частотный интервал между спектральными составляющими

Частотный интервал между спектральными составляющими выражается как f=f_s/N. В таблице B-3 спектр мощности сигнала x[n] обозначен как Sxx. Если N – четное, введем обозначение . В данной таблице приведен формат последовательности компонентов Sxx (выходного массива), соответствующей спектру мощности.

Таблица B-3. Интерпретация элементов массива компонентов ДПФ/БПФ

Элемент массива	Интерпретация
Sxx[0]	Мощность постоянной составляющей
Sxx[2] = Sxx[N–1]	Мощность на частоте f
Sxx[3] = Sxx[N–2]	Мощность на частоте 2f
Sxx[4] = Sxx[N–3]	Мощность на частоте 3f
…	…
Sxx[p–2] = Sxx[N–(p–2)]	Мощность на частоте (p–2)f
Sxx[p–1] = Sxx[N–(p–1)]	Мощность на частоте (p–1)f
Sxx[p]	Мощность на частоте Найквиста

На рис. B-7 приведен спектр мощности в соответствии с таблицей B-3 для синусоидального сигнала амплитудой 2 В, у которого число отсчетов N = 8.

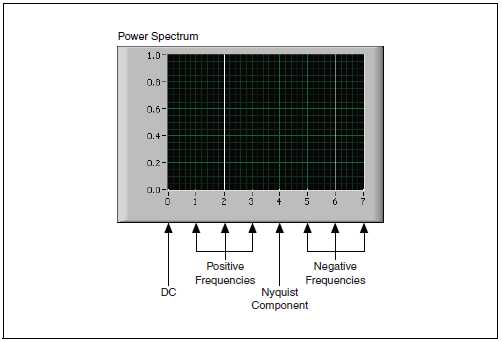
Рисунок B-7. Спектр мощности для N = 8

Power Spectrum – спектр мощности; DC – постоянная составляющая, Positive Frequencies – положительные частоты, Nyquist Component – частота Найквиста, Negative Frequencies – отрицательные частоты

Результат вычисления спектра мощности имеет размерность В²_rms (квадрат среднеквадратического напряжения). Так, если амплитуда входного сигнала (пиковое значение – peak) равна V_pk = 2 В, его среднеквадратическое значение V_rms = , т.е. . Это значение равномерно распределяется между спектральными составляющими в области положительных и отрицательных частот (рис. B-7).

Для нечетного N введем обозначение . В таблице B-4 приведен формат последовательности Sxx на выходе ДПФ/БПФ (выходного массива), соответствующей спектру мощности.

Таблица B-4. Интерпретация элементов выходного массива ДПФ/БПФ

Элемент массива	Интерпретация
Sxx[0]	Мощность постоянной составляющей
Sxx[1] = Sxx[N–1]	Мощность на частоте f
Sxx[2] = Sxx[N–2]	Мощность на частоте 2f
Sxx[3] = Sxx[N–3]	Мощность на частоте 3f
…	…
Sxx[p–2] = Sxx[N–(p–2)]	Мощность на частоте (p–2)f
Sxx[p–1] = Sxx[N–(p–1)]	Мощность на частоте (p–1)f
Sxx[p]= Sxx[p]	Мощность на частоте pf

На рис. B-8 приведен спектр мощности в соответствии с таблицей B-4 для N = 7.

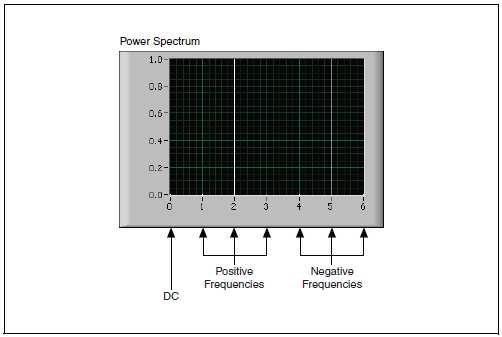
Рисунок B-8. Спектр мощности для N = 7

Power Spectrum – спектр мощности; DC – постоянная составляющая, Positive Frequencies – положительные частоты, Negative Frequencies – отрицательные частоты

Express VI Spectral Measurements

Express VI Spectral Measurements, расположенный на палитре Signal Analysis, позволяет легко выполнять измерения различных спектральных характеристик сигнала. К таким измерениям, в том числе, относятся получение спектра мощности и пикового значения сигнала. С помощью страницы конфигурирования Express VI настраивается тип спектра: амплитудный, среднеквадратический, спектр мощности или спектральная плотность мощности, а также режим вычислений: линейный или логарифмический (дБ). Кроме того, вы можете задать тип окна, параметры усреднения и разрешить отображение спектра фазы. За более подробной информацией об окнах обратитесь к разделу Растекание спектра и сглаживающие окна.

E. Растекание спектра и сглаживающие окна

В практических приложениях вы можете получить только конечное количество отсчетов измеряемого сигнала. Когда вы применяете ДПФ/БПФ для нахождения частотного состава сигнала, делается допущение, что данные представляют собой один период периодически повторяющегося сигнала (рис. B-9). На этом рисунке дискретизации подвергается первый период. Затем сигнал, соответствующий этому периоду, периодически повторяется по оси времени.

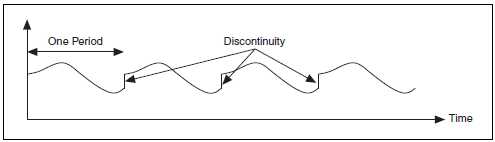
Рисунок B-9. Разрывы (Discontinuity) в повторяющейся выборке сигнала

В связи с тем, что принято допущение о периодичности сигнала, между соседними периодами появляются точки разрыва. Такое явление возникает, когда вы подвергаете дискретизации нецелое количество периодов. Эти искусственные точки разрыва проявляются в спектре в виде паразитных составляющих на очень высоких частотах, которых нет в исходном сигнале. Частоты таких компонент могут быть выше частоты Найквиста и, как вы уже видели ранее, они создадут ложные спектральные составляющие где-нибудь в диапазоне между 0 и fs/2. Таким образом, спектр, полученный с помощью ДПФ/БПФ, не будет соответствовать действительному спектру исходного сигнала, т.е. он будет «размазанным». Это проявляется так, будто бы энергия одной спектральной составляющей «растеклась» по другим частотам. Такое явление называют растеканием (или утечками) спектра.

На рис. B-10 изображен синусоидальный сигнал и соответствующее ему преобразование Фурье. Дискретизированный во временной области сигнал показан на графическом индикаторе Graph 1. Поскольку преобразование Фурье требует периодичности сигнала, то этот сигнал должен быть периодически продолжен во времени, как это показано на индикаторе Graph 2. Соответствующее спектральное представление этого сигнала приведено на индикаторе Graph 3. Поскольку запись сигнала во времени на индикаторе Graph 2 является периодической и не имеет точек разрыва, ее спектр состоит из одной линии, соответствующей частоте исходного сигнала. Отсутствие точек разрыва на индикаторе Graph 2 обусловлено дискретизацией в течение целого количества периодов, в нашем случае одного периода.

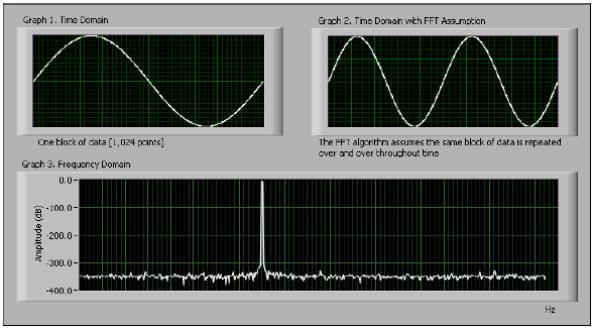
Рисунок. B-10. Синусоидальный сигнал и его преобразование Фурье

На рис. B-11 приведен спектр для сигнала, который продискретизирован на нецелом количестве периодов, например 1.25. Теперь на индикаторе Graph 1 видны 1.25 периода синусоидального сигнала. Если такой сигнал периодически продолжить, то результирующий сигнал на индикаторе Graph 2 содержит разрывы. Соответствующий спектр выведен на индикатор Graph 3, на котором энергия растекается по широкому диапазону частот. Это и есть растекание спектра, т.е. энергия от одной из линий (гармоники) БПФ растекается по всем другим гармоникам.

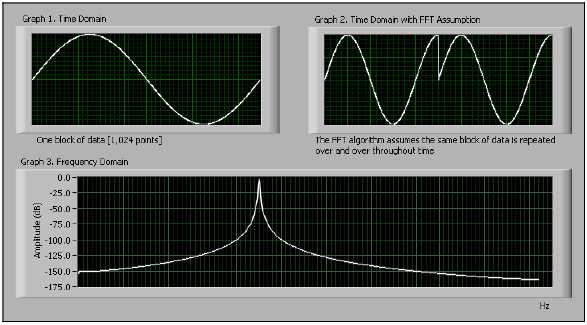
Рисунок B-11. Спектральное представление сигнала при дискретизации нецелого количества периодов исходного сигнала

Растекание спектра имеет место вследствие конечного времени регистрации сигнала. Одним из путей преодоления этого эффекта является регистрация сигнала в течение бесконечного интервала времени, от – до +, результатом чего будет вычисление с помощью БПФ одной линии на соответствующей частоте. Но поскольку время регистрации сигнала ограничено, то для уменьшения растекания спектра применяют так называемые оконные функции.

Степень растекания спектра зависит от перепада сигнала в точке разрыва. Чем больше перепад, тем сильнее растекание, и наоборот. Для уменьшения перепадов в точках разрыва на границах каждого периода можно применять оконные функции. Наложение оконной функции заключается в умножении записи сигнала во временной области на оконную функцию конечной длины, амплитуда которой гладко и плавно изменяется до нуля по краям. Это демонстрируется на рис. B-12, где на исходный сигнал во временной области накладывается окно Хэмминга. Сигнал после наложения оконной функции плавно спадает до нуля по краям. При спектральном анализе конечного количества отсчетов вы можете использовать оконные функции для сведения к минимуму перепадов в точках разрыва дискретизируемого сигнала. Сглаживающая оконная функция, примененная к данным до их преобразования в частотную область, сводит до минимума эффект растекания спектра.

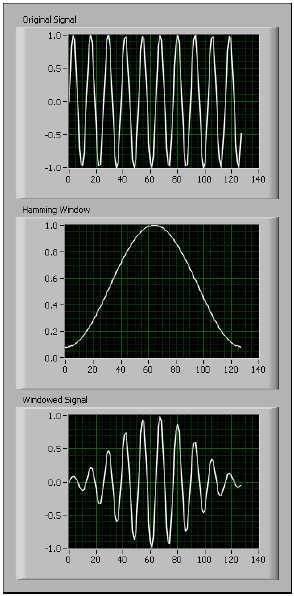
Рисунок B-12. Наложение оконной функции Хэмминга на исходный сигнал

Original Signal – исходный сигнал, Hamming Window – оконная функция Хэмминга, Windowed Signal – сигнал с наложенной оконной функцией

Если запись сигнала во времени состоит из целого количества периодов (рис. B-10), то допущение о периодичности не приводит к появлению точек разрыва, и следовательно, эффект растекания спектра в данном случае отсутствует. Проблема возникает только при наличии нецелого количества периодов.

Есть несколько причин, по которым следует применять оконные функции:

• Необходимость задания времени наблюдения сигнала

• Уменьшение растекания спектра

• Разделение сигнала с малой амплитудой от сигнала с большой амплитуды, когда эти сигналы имеют очень близкие частоты

F. Характеристики различных типов оконных функций

Наложение окна на сигнал во временной области эквивалентно умножению данного сигнала на оконную функцию. Поскольку умножение сигналов во временной области соответствует свертке в частотной области, спектр сигнала с наложенным окном является сверткой спектра исходного сигнала и спектра окна. Наложение окна изменяет форму сигнала во временной области и влияет на наблюдаемый вами спектр.

В зависимости от приложения, одно из окон может оказаться более полезным, чем другие. При использовании Express VI Spectral Measurements вы можете выбрать одной из следующих окон: rectangular (none), Hanning, Hamming, Blackman-Harris, Exact Blackman, Blackman, Flat Top, 4 Term B-Harris, 7 Term B-Harris, Low Sidelobe. Кроме того, в палитре Analyze»Signal Processing»Windows доступны оконные функции Exponential, General Cosine, Cosine Tapered, Force, Kaiser-Bessel и Triangle.

Rectangular (None)

Прямоугольная оконная функция равна единице на всем временном интервале. Математически ее можно записать как

для n = 0, 1, 2, … N – 1

где N – длина окна. Применение прямоугольного окна эквивалентно не использованию вообще какого-либо окна, поскольку прямоугольная функция обрезает сигнал в конечном временном интервале. Такое окно дает самое большую степень растекания спектра. На рис. B-13 приведено прямоугольное окно для N = 32.

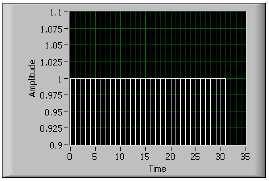
Рисунок B-13. Прямоугольное окно

Прямоугольное окно полезно применять для анализа перепадов, длительность которых короче длительности окна. Его также используют для того, чтобы отслеживать скорость вращения вала машины и, в зависимости от скорости, регулировать частоту дискретизации. В подобных приложениях такая регулировка позволяет обнаруживать основную компоненту вибрации машины и связанные с ней гармоники.

Hanning

Окно Ханнинга имеет форму, похожую на полупериод косинусоидального сигнала и определяется уравнением:

w[n] = 0.5 – 0.5 cos(2n/N) для n = 0, 1, 2, …, N – 1

На рис. B-14 приведено окно Ханнинга для N = 32.

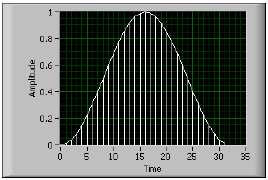
Рисунок B-14. Окно Ханнинга

Окно Ханнинга полезно применять для анализа перепадов, длительность которых больше длительности окна, а также в приложениях общего назначения.

Hamming

Окно Хэмминга является модифицированной версией окна Ханнинга. Его форма также похожа на форму косинусоидального сигнала и определяется выражением:

w[n] = 0.54 – 0.46 cos(2n/N) для n = 0, 1, 2, …, N – 1

На рис. B-15 приведено окно Хэмминга для N = 32.

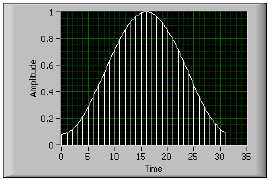
Рисунок B-15. Окно Хэмминга

Окна Ханнинга и Хэмминга чем-то похожи. Но во временной области окно Хэмминга не приближается по краям вплотную к нулю, как окно Ханнинга.

Blackman-Harris

Окно Блэкмана-Харриса, также как и окно Ханнинга, целесообразно использовать для измерения низкоуровневых составляющих, например, искажений, в большом входном сигнале.

Окно Блэкмана-Харриса состоит из трех слагаемых:

w[n] = 0.422323 – 0.49755 cos(2n/N) + 0.07922 cos(4n/N)

для n = 0, 1, 2, …, N – 1.

На рис. B-16 приведено окно Блэкмана-Харриса для N = 32.

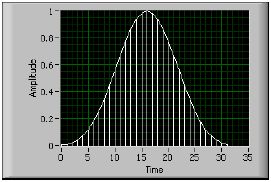
Рисунок B-16. Окно Блэкмана-Харриса

Exact Blackman

Точное окно Блэкмана такое же, как и окно Блэкмана-Харриса, только у него меньший спад на концах. Его можно определить как

w[n] = a₀ – a₁ cos(2n/N) + a₂ cos(4n/N)

для n = 0, 1, 2, …, N – 1.

a₀ = 7938/18608

a₁ = 9240/18608

a₂ = 1430/18608

На рис. B-17 приведено точное окно Блэкмана для N = 32.

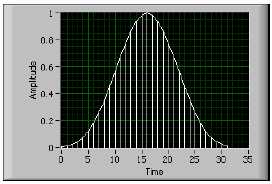
Рисунок B-17. Точное окно Блэкмана

Blackman

Окно Блэкмена похоже на окна Ханнинга и Хэмминга, но оно имеет дополнительную косинусную компоненту, которая еще сильнее уменьшает пульсации. Его можно определить как

w[n] = 0.42 – 0.5 cos(2n/N) + 0.08 cos(4n/N)

для n = 0, 1, 2, …, N – 1.

На рис. B-18 приведено окно Блэкмана для N = 32.

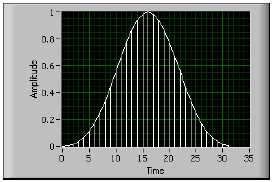
Рисунок B-18. Окно Блэкмана

Flat Top

Окно с плоской вершиной состоит из большего количества косинусных составляющих, чем любое из других окон, изученных ранее. Вторая гармоническая компонента обуславливает опускание оконной функции ниже нуля. Это окно определяется выражением

w[n] = 0.21557895 – 0.41663158 cos(2n/N) + 0.277263158 cos(4n/N) – 0.083578947 cos(6n/N) + 0.006947368 cos(8n/N)

для n = 0, 1, 2, …, N – 1.

На рис. B-19 приведено окно с плоской вершиной для N = 32.

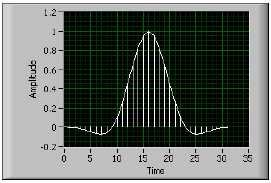
Рисунок B-19. Окно с плоской вершиной

4 Term B-Harris

Четырех-комопнентное окно Блэкмана-Харриса является расширением обычного окна Блэкмана-Харриса путем добавления еще одной косинусной составляющей. Такое окно можно определить как

w[n] = 0.35875 – 0.48829 cos(2n/N)

+ 0.14128 cos(4n/N) – 0.01168 cos(6n/N)

для n = 0, 1, 2, …, N – 1.

На рис. B-20 приведено окно Блэкмана-Харриса-4 для N = 32.

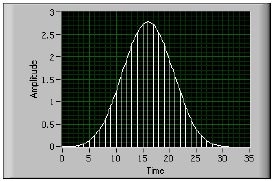
Рисунок B-20. Окно Блэкмана-Харриса-4

7 Term B-Harris

Семи-комопнентное окно Блэкмана-Харриса является расширением обычного окна Блэкмана-Харриса путем добавления четырех косинусных составляющих. Его можно определить как

w[n] = 0.27105 – 0.43329 cos(2n/N) + 0.21812 cos(4n/N)

– 0.06593 cos(6n/N) + 0.01081 cos(8n/N)

– 7.7658E–4 cos(10n/N) + 1.3887E–5 cos(12n/N)

для n = 0, 1, 2, …, N – 1.

На рис. B-21 приведено окно Блэкмана-Харриса-7 для N = 32.

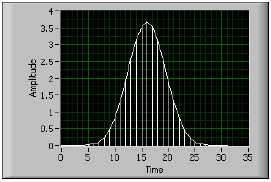
Рисунок B-21. Окно Блэкмана-Харриса-7

Low Sidelobe

Окно с низким уровнем боковых лепестков еще больше уменьшает уровень основного лепестка. Это окно можно определить как

w[n] = 0.323215218 – 0.471492057 cos(2n/N) + 0.17553428 cos(4n/N) – 0.028497078 cos(6n/N) + 0.001261367 cos(8n/N)

для n = 0, 1, 2, …, N – 1.

На рис. B-22 приведено окно с низким уровнем боковых лепестков для N = 32.

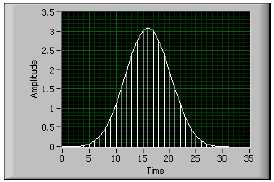
Рисунок B-22. Окно с низкими боковыми лепестками

G. Выбор типа окна, который необходимо использовать

Тип выбираемого вами окна зависит от типа сигнала и от того, что вы исследуете. Для правильного выбора окна требуется знать анализируемый сигнал. В таблице B-5 приведены различные типы сигналов и окна, которые можно вместе с ними использовать.

Таблица B-5.Окна для различных типов сигналов

Тип сигнала	Окно
Перепады, длительность которых меньше длительности окна	Прямоугольное
Перепады, длительность которых больше длительности окна	Ханнинга
Приложения общего назначения	Ханнинга
Отслеживание последовательности	Прямоугольное
Системный анализ (измерения частотных характеристик)	Ханнинга (для случайного воздействия), прямоугольное (для псевдослучайного воздействия)
Разделение двух гармоник с очень близкими друг к другу частотами, но с сильно отличающимися амплитудами	Кайзера-Бесселя
Разделение двух гармоник с очень близкими друг к другу частотами, но почти одинаковыми амплитудами	Прямоугольное

Если у вас недостаточно априорных сведений о сигнале, то следует поэкспериментировать с различными окнами, чтобы найти наиболее подходящее.

Таблица B-6.Описание окон

Окно	Уравнение	Форма	Приложения
Прямоугольное (отсутствие окна)			Перепады, длительность которых меньше длительности окна; отслеживание последовательности; разделение двух гармоник с близкими частотами, и почти одинаковыми амплитудами; анализ реакции системы на воздействие
Ханнинга	w[n] = 0.5 – 0.5 cos(2n/N)		Приложения общего назначения; системный анализ; перепады, длительность которых больше длительности окна;
Хэмминга	w[n] = 0.54 – 0.46 cos(2n/N)		
Блэкмана-Харриса	w[n] = 0.422323 – 0.49755 cos(2n/N) + 0.07922 cos(4n/N)		Те же, что у Блэкмана
Точное Блэкмана	w[n] = 7938/18608 – 9240/18608 cos(2n/N) + 1430/18608 cos(4n/N)		Те же, что у Блэкмана

Таблица B-6.Описание окон (продолжение)

Блэкмана	w[n] = 0.42 – 0.5 cos(2n/N) + 0.08 cos(4n/N)		Перепады сигналов; те же, что у Ханнинга и Хэмминга, но добавляется еще одна косинусная составляющая для уменьшения пульсаций
С плоской вершиной	w[n] = 0.21557895 – 0.41663158 cos(2n/N) + 0.277263158 cos(4n/N) – 0.083578947 cos(6n/N) + 0.006947368 cos(8n/N)		Точные измерения амплитуды отдельной гармоники, когда рядом с ней нет больше никаких частотных составляющих
Блэкмана-Харриса-4	w[n] = 0.35875 – 0.48829 cos(2n/N) + 0.14128 cos(4n/N) – 0.01168 cos(6n/N)		Те же, что у Блэкмана
Блэкмана-Харриса-7	w[n] = 0.27105 – 0.43329 cos(2n/N) + 0.21812 cos(4n/N) – 0.06593 cos(6n/N) + 0.01081 cos(8n/N) – 7.7658E–4 cos(10n/N) + 1.3887E–5 cos(12n/N)		Те же, что у Блэкмана
С низким уровнем боковых лепестков	w[n] = 0.323215218 – 0.471492057 cos(2n/N) + 0.17553428 cos(4n/N) – 0.028497078 cos(6n/N) + 0.001261367 cos(8n/N)		

H. Фильтрация

Фильтрация – это процесс, в результате которого изменяется спектральный состав сигнала. Это один из наиболее распространенных приемов обработки сигналов. В качестве примера из повседневной жизни можно привести регулировку тембра высоких и низких частот в стереосистеме. При изменении положения регуляторов тембра происходит настоящая фильтрация аудио сигнала. В качестве других приложений, где полезна фильтрация, можно упомянуть подавление помехи и выполнение децимации (низкочастотной фильтрации сигнала и уменьшения частоты дискретизации).