Измерение деформации с помощью тензодатчика

Деформации, которые превышают несколько m ( × 10^-3), измеряются редко. Поэтому при измерении деформации требуется точно измерять очень маленькие изменения сопротивления. Предположим, например, что испытуемый образец подвергается сильной деформации в 500 . У датчика с коэффициентом тензочувствительности GF = 2 наблюдается относительное изменение электрического сопротивления только на 2 ×(500 ×10–6) = 0.1%. Для датчика с номинальным сопротивлением 120 Ом соответствующее абсолютное изменение сопротивления составляет 0.12 Ом.

Чтобы измерять такие маленькие изменения сопротивления и компенсировать температурную чувствительность, о которой речь шла в предыдущем разделе, тензодатчики всегда включаются в мостовую схему, на которую подано питание от источника напряжения или тока. Обычный мост Уитстона (рис. 7-14) состоит из четырех резистивных плеч. К одной из диагоналей моста подключен источник питающего напряжения V_EX.

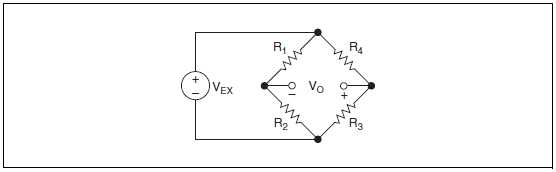
Рисунок 7-14. Обычный мост Уитстона

Выходное напряжение моста вычисляется по формуле:

Здесь очевидно, что если R₁/R₂ = R₃/R₄, то напряжение V_O равно нулю. Говорят, что при выполнении этих условий мост находится в состоянии равновесия (сбалансирован). Любое изменение сопротивление какого-либо из плеч моста приводит к появлению на выходе ненулевого напряжения. Таким образом, если вы замените резистор R₄ на активный тензодатчик (рис. 7-15), то любое изменение сопротивления этого датчика выведет мост из равновесия, и напряжение на выходе моста станет не равным нулю. Если номинальное сопротивление тензодатчика обозначено R_G, а изменение сопротивления, вызванное деформацией – R, то выражение для R можно записать так: R = R_G × GF × . Полагая R₁ = R₂ и R₃ = R_G, из уравнения моста, приведенного выше, можно выразить отношение V_O/V_EX как функцию деформации:

.

Обратите внимание на то, что наличие множителя 1/(1 + GF × /2) указывает на нелинейный характер зависимости выходного напряжения четвертьмостовой схемы от деформации.

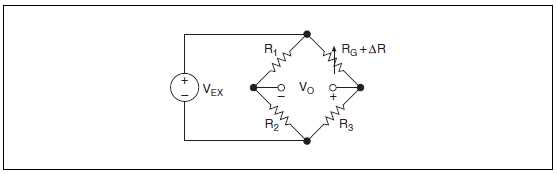
Рисунок 7-15. Схема моста с активным тензодатчиком вместо резистора

Включение в мостовую схему двух тензодатчиков (тензочувствительных элементов) позволяет избежать влияния температуры. Например, на рис. 7-16 приведена схема, где один из датчиков является активным (R_G+R), а второй датчик размещен перпендикулярно направлению деформации. поэтому деформация мало влияет на второй датчик, называемый пассивным датчиком. Однако любые изменения температуры одинаково влияют на оба датчика. В связи с этим отношение их сопротивлений не изменяется, напряжение V_O остается постоянным, и влияние изменений температуры сводится к минимуму.

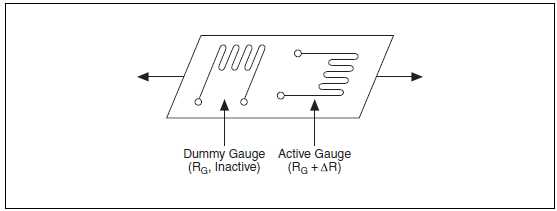
Рисунок 7-16. Активный (Active) и пассивный (Dummy) тензодатчики

В качестве альтернативы можно увеличить чувствительность моста к деформации в два раза, сделав оба датчика активными, хотя и в разных направлениях. На рис. 7-17 показана гнущаяся балка с одним датчиком (R_G + R), смонтированным по направлению растяжения, и другим датчиком (R_G – R), смонтированным по направлению сжатия. На выходе этой полумостовой схемы (рис. 7-17) зависимость напряжения от деформации более линейна, а значение напряжения примерно в два раза превышает напряжение на выходе четвертьмостовой схемы:

.

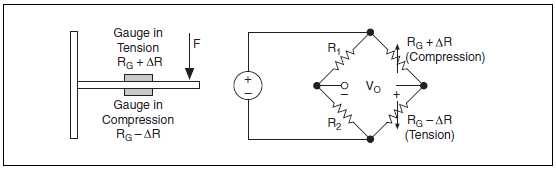
Рисунок 7-17. Полумостовая схема

Gauge in Tension – датчик в направлении растяжения, Gauge in Compression – датчик в направлении сжатия, Compression – сжатие, Tension – растяжение

Наконец, вы можете еще больше увеличить чувствительность схемы, включив во все плечи моста активные тензодатчики. Два из них монтируются по направлению растяжения, а остальные два – по направлению сжатия. На рис.7-18 приведена полномостовая схема.

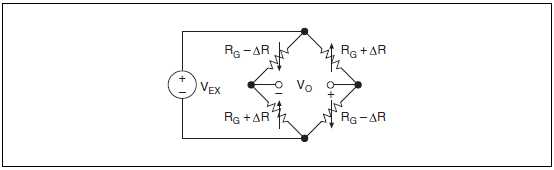
Рисунок 7-18. Полномостовая схема

.

Уравнения, приведенные здесь для схем на основе моста Уитстона, подразумевают, что изначально мост находится в состоянии равновесия, и что он выдает на выходе нулевое напряжение, если нет никакой деформации. Однако, на практике из-за отклонений сопротивлений резисторов и деформации, обусловленной креплением датчика, возникает некоторое начальное напряжение смещения. Это напряжение обычно корректируется двумя способами. Во-первых, для восстановления равновесия моста вы можете использовать специальную балансировочную схему, с помощью которой регулируется сопротивление моста и выходное напряжение приводится к нулю. Во вторых вы можете измерить начальное напряжение при отсутствии деформации и компенсировать его программным путем. Уравнения измерения деформации для четвертьмостовой (Quarter-Bridge), полумостовой (Half-Bridge) и полномостовой (Full-Bridge) схем с учетом начальных напряжений смещения приведены в параграфе Уравнения измерения деформации. В этих уравнениях учитывается также влияние сопротивлений подводящих проводников.