Вычисление весов превышений
Таблица 11
Номер измерения |
Длина, измеренная на карте, (км) |
Коэффициент извилистости |
Длина, измеренная на местности, (км) |
Вес превышения |
h1 |
0,675 |
1,1 |
0,743 |
1,35 |
h2 |
0,65 |
1,1 |
0,715 |
1,40 |
h3 |
1,325 |
1,2 |
1,590 |
0,63 |
h4 |
1,35 |
1,1 |
1,485 |
0,67 |
h5 |
1,325 |
1,2 |
1,590 |
0,63 |
h6 |
1,2 |
1,1 |
1,320 |
0,76 |
h7 |
0,675 |
1,1 |
0,743 |
1,35 |
h8 |
0,65 |
1,1 |
0,715 |
1,40 |
После вычисления по программе "ОМ" матрица весовых коэффициентов будет иметь следующий вид:
Qtxt = Q5x5= |
|
δHN |
δHK |
δHD |
δHL |
δHC |
δHN |
0,5259 |
0,2072 |
0,3925 |
0,3247 |
0,3581 |
|
δHK |
|
0,5145 |
0,3358 |
0,4011 |
0,3690 |
|
δHD |
|
|
1,2369 |
0,9072 |
1,0692 |
|
δHL |
|
|
|
1,2035 |
1,0581 |
|
δHC |
|
|
|
|
1,4173 |
На основании анализа диагональных элементов матрицы Q можно отметить, что наиболее слабым репером, относительно которого необходимо выполнять оценку точности, является Рn C. А необходимая точность измерения превышений на 1 км хода может быть вычислена по формуле:
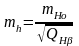(12)
mh = |
2.4 |
мм |
Следовательно, при построении нивелирной сети первой степени необходимо применять инструменты и методику измерений, соответствующие II классу геометрического нивелирования со средней квадратической ошибкой измерения превышения на 1 км хода - 2 мм.
Для нивелирной сети второй степени, изображённой на рис. 12, матрица параметрических уравнений поправок выглядит следующим образом:
Anxt = A5x4= |
|
δH1 |
δH2 |
δH3 |
δH4 |
δh9 |
0 |
0 |
0 |
0 |
|
δh10 |
-1 |
0 |
-1 |
0 |
|
δh11 |
0 |
-1 |
+1 |
+1 |
|
δh12 |
1 |
0 |
0 |
0 |
|
δh13 |
0 |
+1 |
0 |
-1 |
а веса запроектированных измерений имеют следующие численные значения:
Таблица 12