Определение наиболее слабого пролёта
Название опор |
QXi |
QXi + QXi+1 |
QYi |
QYi + QYi+1 |
I |
0,1814 |
|
0,0987 |
|
|
|
0,4006 |
|
0,1918 |
II |
0,2165 |
|
0,0747 |
|
|
|
0,3658 |
|
0,2013 |
III |
0,1826 |
|
0,1217 |
|
|
|
0,3325 |
|
0,1417 |
IV |
0,1471 |
|
0,029 |
|
Таким образом, наиболее слабым как по оси абсцисс, так и по оси ординат является пролет между опорами II-III. Подставляя максимальные суммы диагональных элементов в формулы (9), получим
μраз= |
1,2 |
s |
mβраз= |
1,2 |
s |
|
|
|
|
|
|
μраз= |
0,8 |
s |
mβраз= |
0,8 |
s |
Следовательно, углы при разбивке опор прямой угловой засечкой необходимо откладывать по программе полигонометрии 4 класса с mβ = 2".
2.2.2. Расчёт точности в линейной засечке
На стадии возведения тела опоры мостового перехода появляется возможность установить геодезический инструмент вблизи проектного центра.
Поэтому, в этом случае, проектируют другие, более простые в организационном плане способы разбивки.
Это можно сделать одним из трех возможных способов разбивки:
1) обратная угловая засечка;
2) линейная засечка;
3) комбинированная засечка.
Широкое внедрение в топографо-геодезическое производство высокоточных светодальномеров позволяет опоры мостового перехода разбивать линейной засечкой. В этом случае матрица параметрических уравнений поправок А в общем виде для варианта, изображенного на рис. 8, имеет следующий вид:
|
|
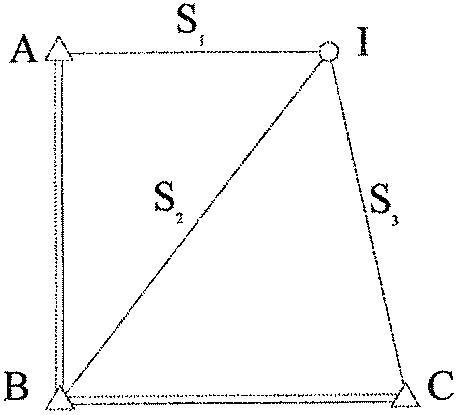
δX1 |
δY1 |
A3X2= |
VS1 |
+cos(αAI) |
+cos(αAI) |
VS2 |
+cos(αBI) |
+cos(αBI) |
|
|
VS3 |
+cos(αCI) |
+cos(αCI) |
Рис. 8. Линейная засечка
Если для нашего варианта разбивка опор мостового перехода предусмотрена линейной засечкой, то один из возможных вариантов, проектирования представлен на рис. 9.
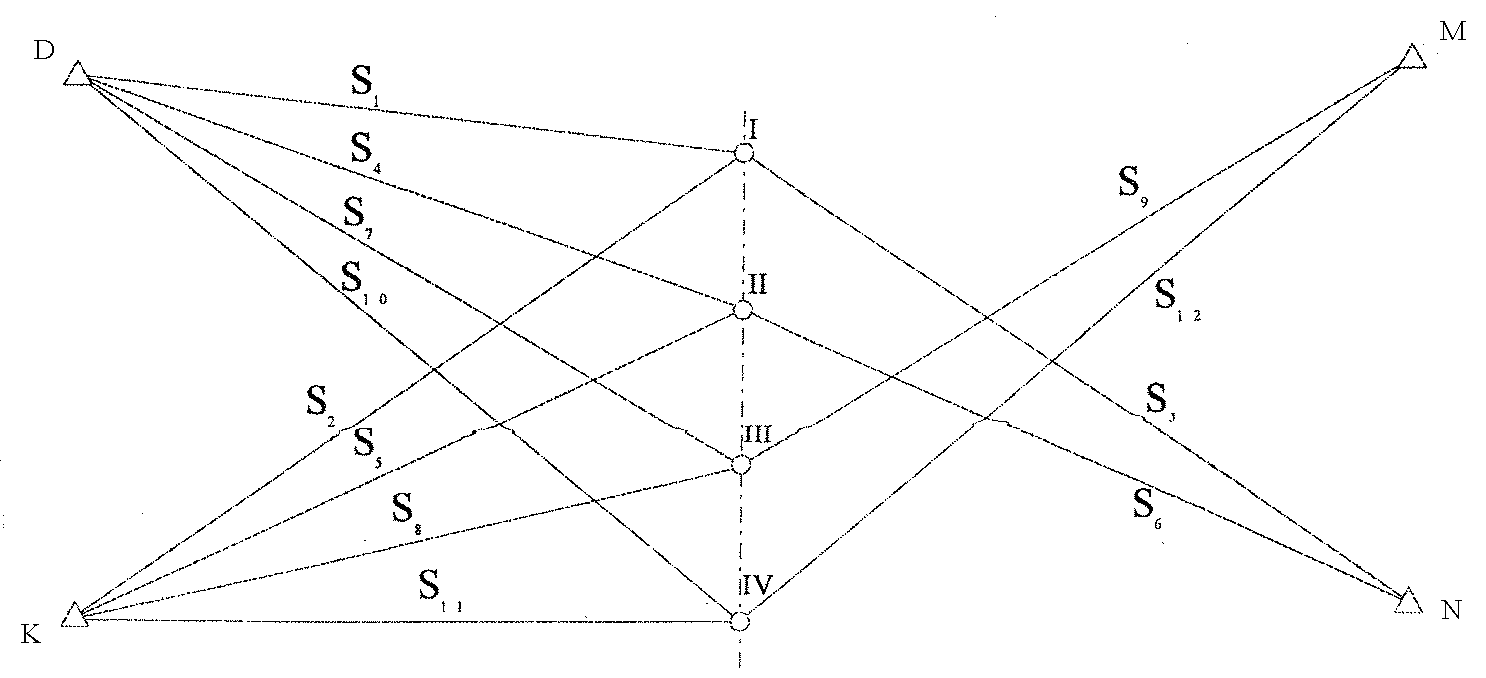
Рис. 9. Проект разбивки опор мостового перехода линейной засечкой
В этом случае матрицы параметрических уравнений А в индексном виде записываются следующим образом:
|
|
δXI |
δYI |
AI |
VS1 |
+cos(α 3I) |
+sin(α 3I) |
VS2 |
+cos(α 1I ) |
+sin(α 1I) |
|
|
VS3 |
+cos(α 2I) |
+sin(α 2I) |
|
|
||
|
|
δXIII |
δYIII |
AIII |
VS7 |
+cos(α 3 III) |
+sin(α 3 III) |
VS8 |
+cos(α 1 III) |
+sin(α 1 III) |
|
|
VS9 |
+cos(α 2 III) |
+sin(α 2 III) |
|
|
δXII |
δYII |
AII |
VS1 |
+cos(α 3 II) |
+sin(α 3 II) |
VS2 |
+cos(α 1 II) |
+sin(α 1 II) |
|
|
VS3 |
+cos(α 2 II) |
+sin(α 2 II) |
|
|
||
|
|
δXIV |
δYIV |
AIV |
|
+cos(α 3 IV) |
+sin(α 3 IV) |
Vs8 |
+cos(α 1 IV) |
+sin(α 1 IV) |
|
|
Vs9 |
+cos(α 2 IV) |
+sin(α 2 IV) |
;
;
Таблица для вычисления коэффициентов
Стороны |
α |
sin α |
cos α |
DI |
280 00 |
-0,94 |
0,34 |
NI |
240 00 |
-0,96 |
-0,26 |
KI |
180 00 |
0,00 |
-1,00 |
DII |
305 00 |
-0,69 |
0.72 |
NII |
229 00 |
-0,91 |
-0.41 |
KII |
180 00 |
0,00 |
-1,00 |
DIII |
315 00 |
-0,59 |
0,81 |
NIII |
241 00 |
-0,93 |
-0.36 |
LIII |
180 00 |
0,00 |
-1,00 |
DIV |
326 00 |
-0,48 |
0.87 |
NIV |
248 00 |
-0,97 |
-0.24 |
LIV |
180 00 |
0,00 |
-1,00 |
В численном виде матрицы параметрических уравнений поправок имеют следующий вид:
|
|
δXI |
δYI |
|
|
|
δXI |
δYI |
AI= |
Vβ1 |
0,530 |
-0,848 |
|
AII= |
Vβ1 |
0,682 |
-0,731 |
|
Vβ2 |
-0,809 |
-0,588 |
|
|
Vβ2 |
-0,719 |
-0,695 |
|
Vβ3 |
-0,839 |
0,545 |
|
|
Vβ3 |
-0,777 |
0,629 |
|
|
δXI |
δYI |
|
|
|
δXI |
δYI |
AIII= |
Vβ1 |
0,743 |
-0,669 |
|
AIV= |
Vβ1 |
0,883 |
-0,469 |
|
Vβ2 |
-0,656 |
-0,755 |
|
|
Vβ2 |
-0,602 |
-0,799 |
|
Vβ3 |
0,719 |
0,695 |
|
|
Vβ3 |
0,766 |
0,643 |
Вычисления по программе "ОМ" привели к следующим матрицам весовых коэффициентов:
|
|
δXI |
δYI |
QI = |
δXI |
0,1841 |
0,0283 |
|
δXI |
|
0,1079 |
|
|
|
|
|
|
δXIII |
δYIII |
QIII = |
δXI |
0,1934 |
-0,0227 |
|
δXI |
|
0,1271 |
|
|
δXII |
δYII |
QII = |
δXI |
0,2065 |
0,0028 |
|
δXI |
|
0,074 |
|
|
|
|
|
|
δXIV |
δYIV |
QIV = |
δXI |
0,1418 |
-0,005 |
|
δXI |
|
0,02 |
;
;
Элементы матриц весовых коэффициентов и вычисления, позволяющие определить наиболее слабые пролёты, приведены в табл. 7.
Таблица 7