2.2. Расчёт точности в геодезических фигурах разбивки
Расчет необходимой точности измерений в запроектированных фигурах разбивки (mβ и ms) выполняется, исходя из допуска (3), который накладывается на СКО проекций межосевого размера S между центрами опор мостового перехода на соответствующие координатные оси.
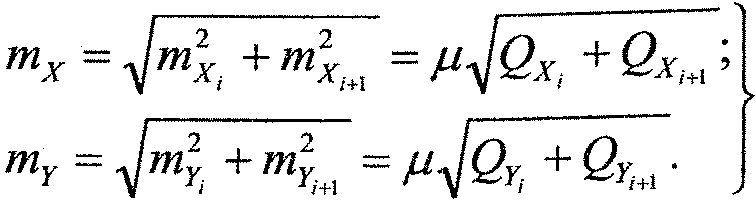
(8)
Заменяя в формулах (7) СКО проекций межосевого размера на установленный допуск на фигуры разбивки (3) и выражая неизвестную СКО единицы веса, получаем
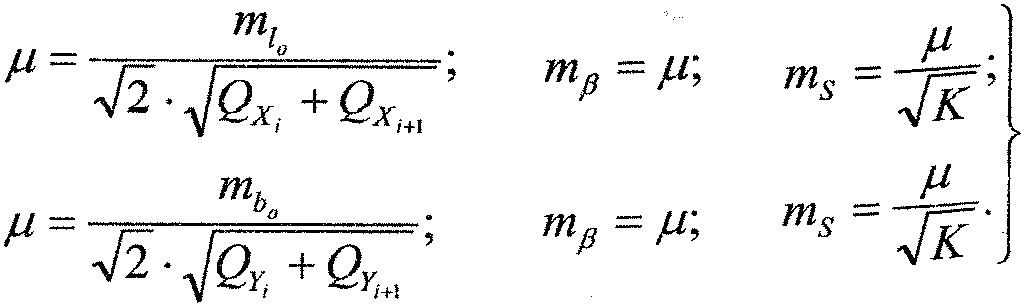
(9)
Следует отметить, что расчет необходимой точности измерения углов и длин линий в фигурах разбивки выполняется относительно наиболее слабого пролета между центрами опор мостового перехода. Наиболее слабым будет являться тот пролёт, который характеризуется максимальной суммой диагональных элементов матриц весовых коэффициентов (QXi + QXi+1 )max и (QYi + QYi+1 )max.
2.2.1. Расчёт точности в прямой угловой засечке
При строительстве мостового перехода такой способ разбивки применяется на стадии возведения фундаментов под тело опор [3]. Общий вид такой фигуры разбивки приведен на рис. 5.
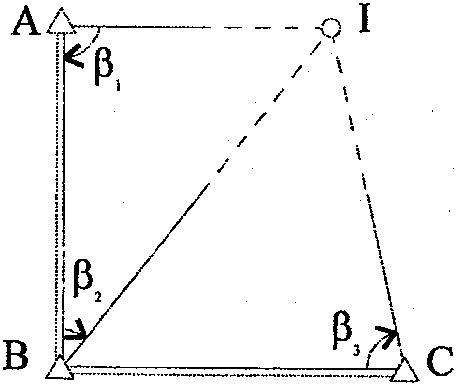
Рис. 5. Геодезическая фигура разбивки в виде прямой угловой засечки
Для расчета необходимой точности измерений в такой фигуре разбивки необходимо составить матрицу параметрических уравнений поправок, имеющую в соответствии с работой [1] следующий вид.
Anxt = A3x2 = |
|
δX1 |
δY1 |
Vβ1 |
-aIA |
-bIA |
|
Vβ2 |
aIB |
bIB |
|
Vβ3 |
aIC |
bIC |
Вычисление коэффициентов матрицы А выполняется по следующим формулам:
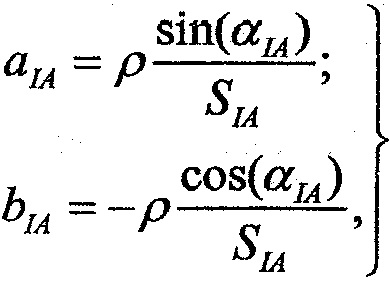
(10)
где аIА, SIА - соответственно, дирекционный угол и длина линии, снимаемые с графической точностью с проекта фигуры разбивки. Размерность SIА должна обеспечивать значения коэффициентов около единицы и быть равной, размерности mlO и тbO в формулах (9).
Используя составленную матрицу параметрических уравнений поправок А для запроектированной фигуры разбивки по программе "ОМ", вычисляют матрицу весовых коэффициентов определяемых параметров Q [1].
Qtxt = Q2x2 = |
|
δX1 |
δY1 |
δX1 |
QX1 |
QX1Y1 |
|
δX1 |
|
QY1 |
Диагональные элементы матрицы Q характеризуют точность разбиваемой опоры соответственно по оси X и по оси Y. Пусть для разбивки четырех опор мостового перехода запроектированы геодезические фигуры разбивки в виде четырёх прямых угловых засечек, изображенных на рис. 6.
В качестве исходных для проектирования фигур разбивки необходимо выбирать такие пункты ИГС, которые обеспечивают выполнение следующих условий:
1. Угол засечки (угол между направлением на исходные пункты с разбиваемой опоры) должен находиться в диапазоне 30° ≤ γ ≤50° .
2. Минимальные длины линий от исходных пунктов, до разбиваемой опоры.
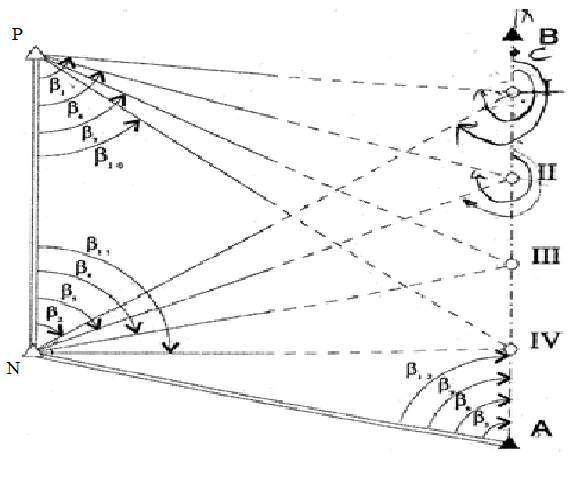
Рис 6. Схема разбивки опор мостового перехода прямой угловой засечкой
Для каждой разбиваемой опоры, в соответствии с работой [1], необходимо составить матрицу параметрических уравнений поправок. Для данного проекта (рис. 6) они будут иметь следующий вид:
В этом случае матрицы параметрических уравнений А в индексном виде записываются следующим образом:
|
|
δXI |
δYI |
AI |
Vβ1 |
- а I D |
- b I D |
Vβ2 |
а I K |
b I K |
|
|
Vβ3 |
а I A |
b I A |
|
|
||
|
|
δXIII |
δYIII |
AIII |
Vβ7 |
- а III D |
- b III D |
Vβ8 |
а III K |
b III K |
|
|
Vβ9 |
а III A |
b III A |
|
|
δXII |
δYII |
AII |
Vβ1 |
- а II D |
- b II D |
Vβ2 |
а II K |
b II K |
|
|
Vβ3 |
а II A |
b II A |
|
|
||
|
|
δXIV |
δYIV |
AIV |
Vβ1 |
- а IV D |
- b IV D |
Vβ2 |
а IV K |
b IV K |
|
|
Vβ3 |
а IV A |
b IV A |
;
;
Для вычисления коэффициентов матрицы А целесообразно составить таблицу следующего вида:
Таблица 3
Таблица для вычисления коэффициентов
Стороны |
α |
sin α |
cos α |
S (см) |
a |
b |
IP |
280 00 |
-0,94 |
0,34 |
900 00 |
-2,41 |
0,88 |
IN |
240 00 |
-0,96 |
-0,26 |
1050 00 |
-1,73 |
-0,46 |
IA |
180 00 |
0,00 |
-1,00 |
800 00 |
0,00 |
-2,36 |
IIP |
305 00 |
-0,69 |
0.72 |
1000 00 |
-1,51 |
1,56 |
IIN |
229 00 |
-0,91 |
-0.41 |
975 00 |
-1,88 |
-0,84 |
IIA |
180 00 |
0,00 |
-1,00 |
725 00 |
0,00 |
-3,06 |
IIIP |
315 00 |
-0,59 |
0,81 |
1100 00 |
-1,10 |
1,52 |
IIIN |
241 00 |
-0,93 |
-0.36 |
900 00 |
-2,20 |
-0,84 |
IIIA |
180 00 |
0,00 |
-1,00 |
525 00 |
0,00 |
-2,06 |
IVP |
326 00 |
-0,48 |
0.87 |
1200 00 |
-0,80 |
1,44 |
IVN |
248 00 |
-0,97 |
-0.24 |
775 00 |
-2,67 |
-0,67 |
IVA |
180 00 |
0,00 |
-1,00 |
400 00 |
0,00 |
-6,88 |
В численном виде матрицы параметрических уравнений поправок имеют следующий вид:
|
|
δXI |
δYI |
|
|
|
δXI |
δYI |
AI= |
Vβ1 |
0,530 |
-0,848 |
|
AII= |
Vβ1 |
0,682 |
-0,731 |
|
Vβ2 |
-0,809 |
-0,588 |
|
|
Vβ2 |
-0,719 |
-0,695 |
|
Vβ3 |
0 |
0,545 |
|
|
Vβ3 |
0 |
0,629 |
|
|
δXI |
δYI |
|
|
|
δXI |
δYI |
|
AIII= |
Vβ1 |
0,743 |
-0,669 |
|
AIV= |
Vβ1 |
0,883 |
-0,469 |
|
|
Vβ2 |
-0,656 |
-0,755 |
|
|
Vβ2 |
-0,602 |
-0,799 |
|
|
Vβ3 |
0 |
0.695 |
|
|
Vβ3 |
0 |
0,643 |
|
Вычисления по программе "ОМ" привели к следующим матрицам весовых коэффициентов:
|
|
δXI |
δYI |
QI = |
δXI |
0,6652 |
0,1531 |
|
δXI |
|
0,7369 |
|
|
|
|
|
|
δXIII |
δYIII |
QIII = |
δXI |
0,6735 |
0,2715 |
|
δXI |
|
0,8693 |
|
|
δXII |
δYII |
QII = |
δXI |
0,7025 |
0,2483 |
|
δXI |
|
0,7962 |
|
|
|
|
|
|
δXIV |
δYIV |
QIV = |
δXI |
0,7256 |
0,1675 |
|
δXI |
|
0,6887 |
;
Для определения наиболее слабого пролета, образуемого центрами опор мостового перехода, относительно которого следует выполнить расчет необходимой точности измерений, запишем диагональные элементы матриц весовых коэффициентов в таблицу следующего вида.
Таблица 4