2. Расчёт необходимой точности измерений в запроектированном геодезическом обосновании

Расчет необходимой точности измерений в исходной сети (m_β и m_s) и фигурах разбивки (m_{β раз} и m_{s раз}) выполняется, исходя из заданного предельного отклонения пролетного строения мостового перехода от проектной длины

Δ_l = 40 мм и ширины Δ_b = 30 мм [4]. Переход от предельных значений к средним квадратическим ошибкам, при доверительной вероятности Р = 95%, выполняется по формулам:

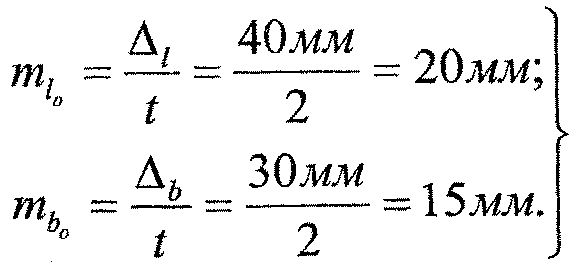
(1)

При расположении оси X параллельно оси мостового перехода заданные СКО можно разложить на следующие составляющие:

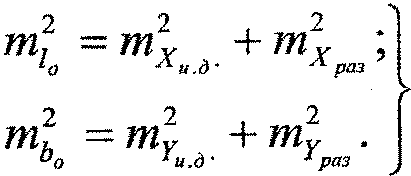
(2)

где m_{X и.д.}, m_{Y и.д.}. - ошибки исходной геодезической сети;

m_{X раз.}; m_{Y раз.} Ошибки фигур разбивки.

Применяя принцип равного влияния, получим допустимые СКО на исходную инженерно - геодезическую сеть и фигуры разбивки

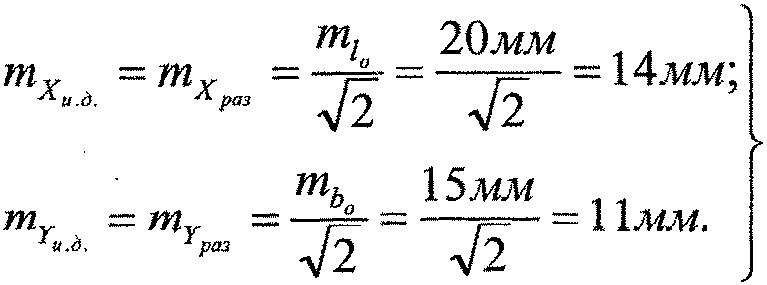
(3)

Допуск на исходную геодезическую сеть относится к СКО положения пункта в наиболее слабом месте по оси X (m_{X и.д.}) и по оси Y (m_{Y и.д.}) относительно ближайшего исходного пункта.

Допуск на фигуры разбивки относится к наиболее грубо определяемой СКО проекции межосевого расстояния между центрами опор мостового перехода на ось абсцисс (m_{X раз}) и ось ординат (m_{Y раз}).

2.1 Расчёт точности в инженерно-геодезических сетях

Расчет необходимой точности измерений (m_β и m_s) в ИГС выполняется, исходя из допустимой СКО положения пункта в наиболее слабом месте (3). Причем допуски на составляющие ошибки по оси абсцисс и ординат разные. Поэтому на основании работы [1] необходимая точность угловых и линейных измерений может быть вычислена по следующим формулам:

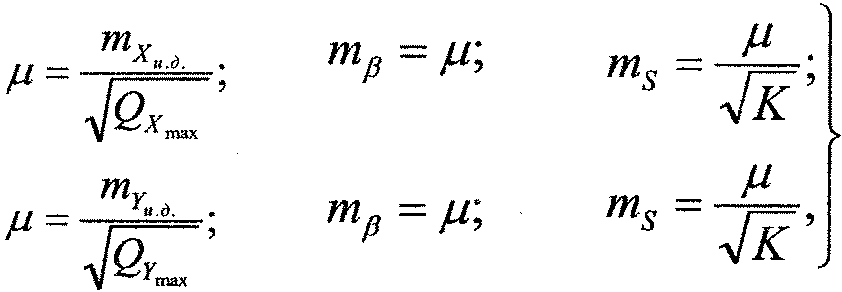
(4)

где Qx_max, Qy_max - соответственно максимальные диагональные элементы матрицы весовых коэффициентов Q;

m_β, m_s - неизвестные средние квадратические ошибки угловых и линейных измерений в ИГС;

К - априорно задаваемый коэффициент соотношения средних квадратических ошибок измерений [1].

(5)

Как показали исследования, выполненные в пособии [1], для ИГС с небольшим числом избыточных измерений коэффициент К целесообразно задавать К > 4.

Пусть в качестве исходной плановой инженерно-геодезической сети запроектировано построение, изображенное на рис. 3.

Для вычисления необходимой точности измерений в запроектированной ИГС необходимо вычислить матрицу весовых коэффициентов Q. Получение такой матрицы наиболее целесообразно выполнять по программе "Prourav". Исходную информацию для работы по программе следует составлять в виде, приведённом в работе [1]. Следует отметить, значение СКО измеренного угла всегда должно задаваться в виде 1, а СКО измеренной линии задано значением 0,5, исходя из априорно заданного коэффициента К = 4 в соответствии с рекомендациями, полученными в работе [1].

На рис. 3 приняты следующие обозначения:

- исходные пункты ИГС, которые в нашем случае совпадают со знаками, закрепляющими ось мостового перехода;

- определяемые пункты;

- измеренные базисы.

Каталог координат

	X	Y
A	67700	14950
B	68600	16100
C	68350	15800
D	67700	16300
E	67075	15700
F	68200	14450
J	68950	15500

Рис. 3. Проект исходной ИГС

В результате вычислений получена следующая матрица весовых коэффициентов: