2. Теоретические сведения

2.1. Классификация динамических звеньев

Элементы, из которых составлены различные системы автоматиче­ского регулирования называются звеньями. Они могут значительно раз­личаться как по физической природе процессов, происходящих в них, так и по своему конструктивному выполнению. Если работа звеньев описы­вается одинаковыми дифференциальными уравнениями, то их к одному типу. При теоретическом исследовании САР последнее положение явля­ется наиболее существенным. Поэтому в теории автоматического регули­рования принято различать элементы по математическому описанию и, в случае совпадения последнего, считать их принадлежащими одному типу так называемых динамических звеньев, из которых составляются структурные схемы САР.

Все звенья по виду своих статических характеристик (т.е. функцио­нальной связи выходной и входной величин после окончания переходных процессов) делятся в основном на три класса: позиционные (или ста­тические), интегрирующие и дифференцирующие.

Дифференциальные уравнения и передаточные функции звеньев САР исследуемых в работе приведены в табл. 1.

Таблица 1. Дифференциальные уравнения и передаточные

функции звеньев САР

В динамическом режиме звенья, относящиеся к одному классу, мо­гут вести себя существенно различно в зависимости от того, какими диф­ференциальными уравнениями они описываются.

Исследование звеньев можно осуществлять и на физических моде­лях в электрических цепях, если математическое описание работы звена и модели совпадает по форме.

В лабораторной работе исследуются четыре звена: позиционные -апериодическое первого порядка и колебательное; интегрирующее перво­го порядка без замедления и дифференцирующее первого порядка с за­медлением. Указанные звенья выполнены в виде простейших электриче­ских цепей, схемы которых показаны на рис.1. Входной величиной X(t) является напряжение U_BX, а выходной Y(t) - напряжение U_ВЫХ.

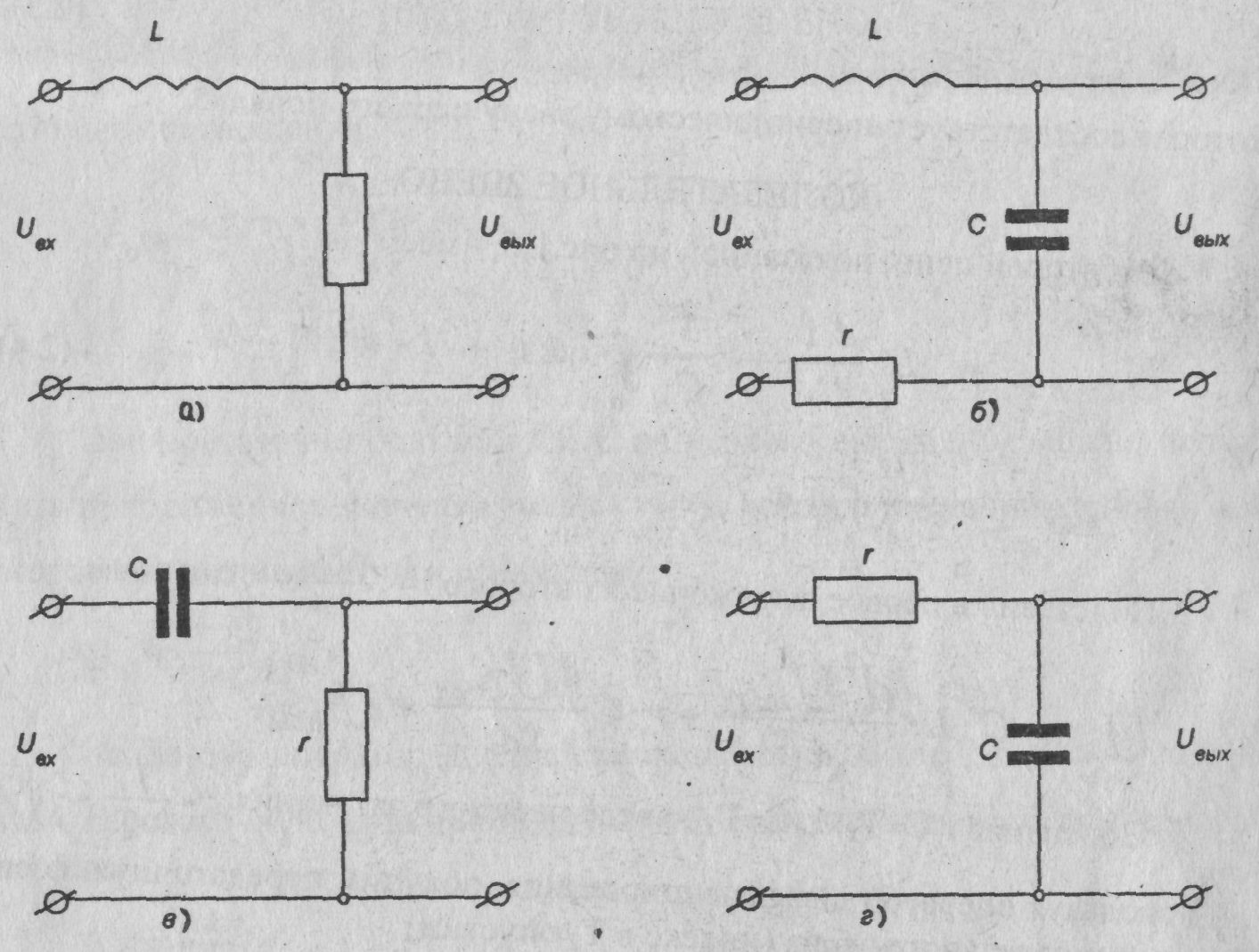
Рис. 1. Принципиальные схемы электрических моделей звеньев

Апериодическое звено 1-го порядка. Действительно, для первой цепи (рис.1,а) можно записать:

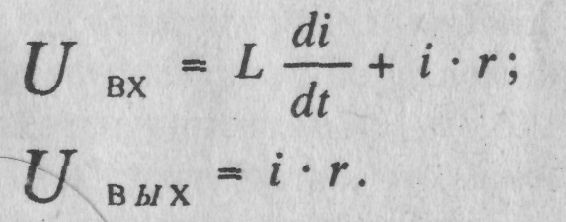(2.1)

Из последнего выражения запишем передаточную функцию

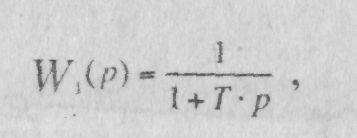(2.3)

которая соответствует апериодическому звену первого порядка.

Колебательное звено. Для второй цепи, показанной на рис. 1,б, имеем

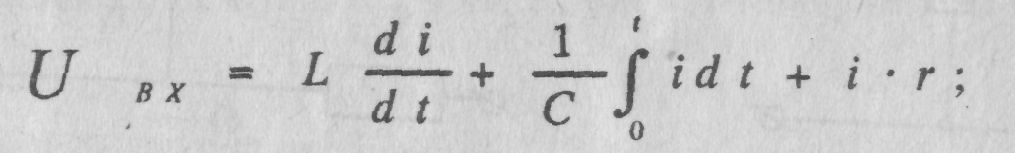(2.4)

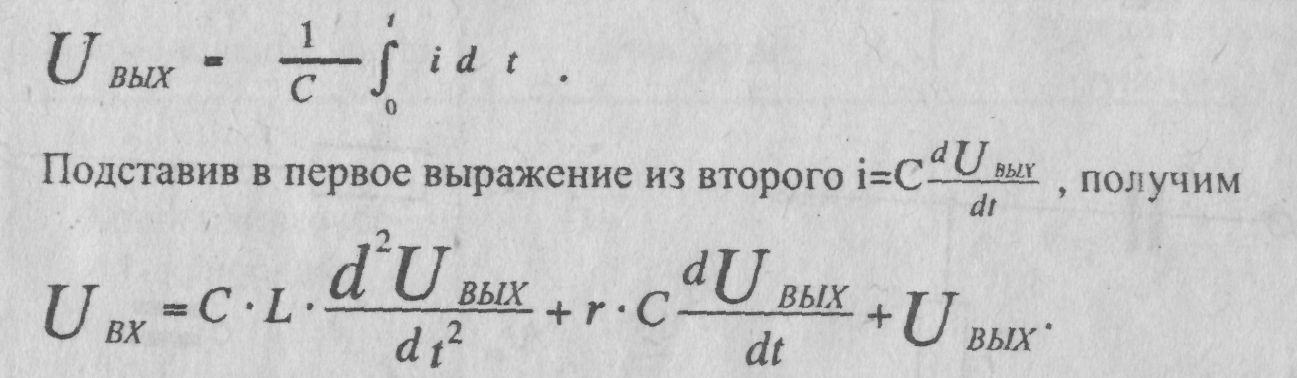
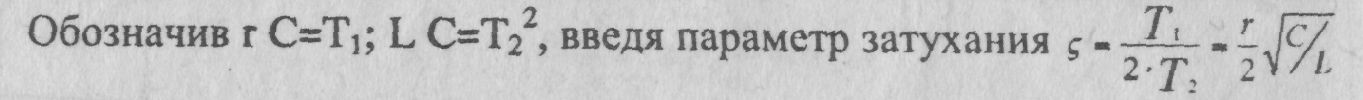
и используя оператор дифференцирования, получим передаточную функ­цию колебательного звена (индекс в Т₂ опустим)

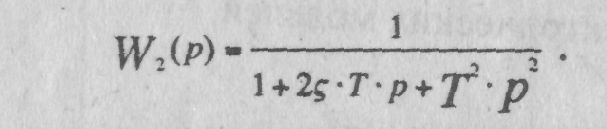(2.5)

Дифференцирующее звено. Для цепи (рис.1,в) можно записать следующие выражения:

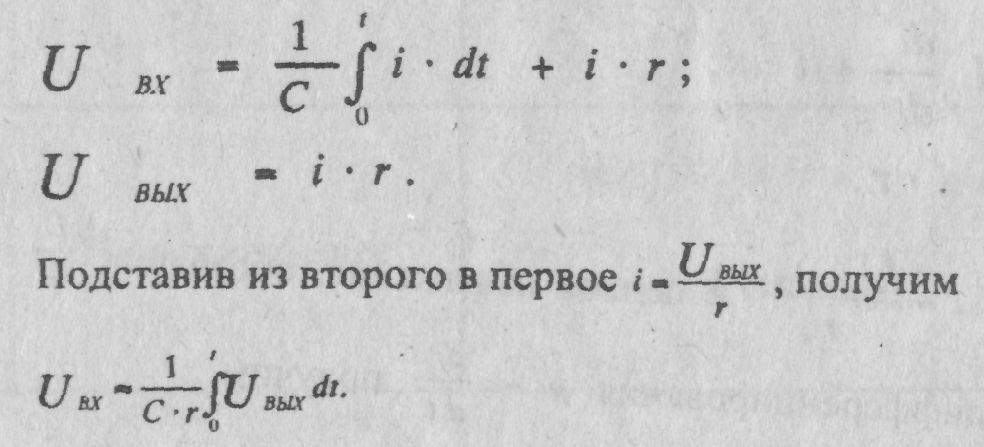(2.6)

Введя оператор дифференцирования р и обозначив rC=k=T получа­ем передаточную функцию дифференцирующего звена с замедлением

W₃(p)=kp. (2.7)

Интегрирующее звено. Для последней цепи, изображенной на рис.1,г, справедливы сле­дующие соотношения:

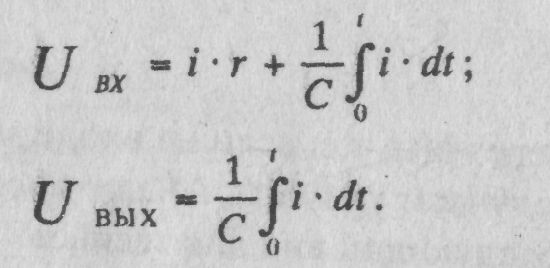(2.8)

При достаточно больших г и С из первого выражения можно полу-

второе уравнение дает нам следующее:

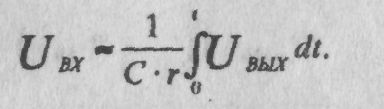
Используя оператор дифференцирования и обозначив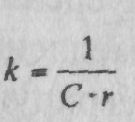

получаем передаточную функцию идеального интегрирующего звена первого порядка

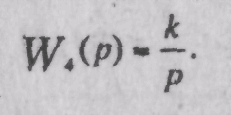(2.9)

В общем случае динамические свойства звеньев САР могут быть описаны либо с помощью дифференциальных уравнений, либо посредст­вом графических характеристик. В теории автоматического регулирова­ния (ТАР) применяются два типа характеристик: временные и частотные.

Удобство их использования заключается в том, что они могут быть построены не только по уравнению (с которым связаны однозначно), но и сняты экспериментально, что очень ценно для практики. Важным являет­ся и то обстоятельство, что можно решить обратную задачу - по экспери­ментальным характеристикам составить дифференциальное уравнение звена.