Строительство и горное дело
Строительство — обмеры зданий, контроль отклонения плоскостей стен и несущих колонн от вертикали (в том числе в динамике), анализ вибраций стен и остекления. Обмеры котлованов, создание трёхмерных моделей стройплощадок для оценки объёмов земляных работ.
Архитектура — построение трёхмерных моделей городской среды для оценки влияния предлагаемых новостроек на облик города.
Морские технологии
Измерение глубины моря. Для этой задачи используется дифференциальный лидар авиационного базирования. Красные волны почти полностью отражаются поверхностью моря, тогда как зелёные частично проникают в воду, рассеиваются в ней, и отражаются от морского дна. Технология пока не применяется в гражданской гидрографии из-за высокой погрешности измерений и малого диапазона измеряемых глубин.
Поиск рыбы. Аналогичными средствами можно обнаруживать признаки косяков рыбы в приповерхностных слоях воды. Специалисты американской государственной лаборатории ESRL утверждают, что поиск рыбы лёгкими самолётами, оборудованных лидарами, как минимум на порядок дешевле, чем с судов, оборудованных эхолотами.
Системы подводного зрения. У истоков подводного применения лидаров на море стояла корпорация Kaman, запатентовавшая работоспособную технологию в 1989 году. Интенсивное (по сравнению с воздушной средой) рассеивание света в воде долгое время ограничивало действие подводных лидаров десятками метров. Импульс лазера способен «пробить» и большие расстояния, но при этом полезный отражённый сигнал оказывается неразличим на фоне паразитной засветки. Kaman преодолела эту проблему с помощью электронных затворов, открывавших оптический путь к CCD-приёмнику только на короткий период ожидаемого отклика.
Промышленные и сервисные роботы
Системы машинного зрения ближнего радиуса действия для роботов, основанные на сканирующем лидаре IBM, формируют цилиндрическую развёртку с углом охвата горизонта 360° и вертикальным углом зрения до +30..-30
Военные технологии
Здесь лидары получили самое широкое распространение и выполняют функции ооптико-локационной локации, разведки, наведения на цель итп.
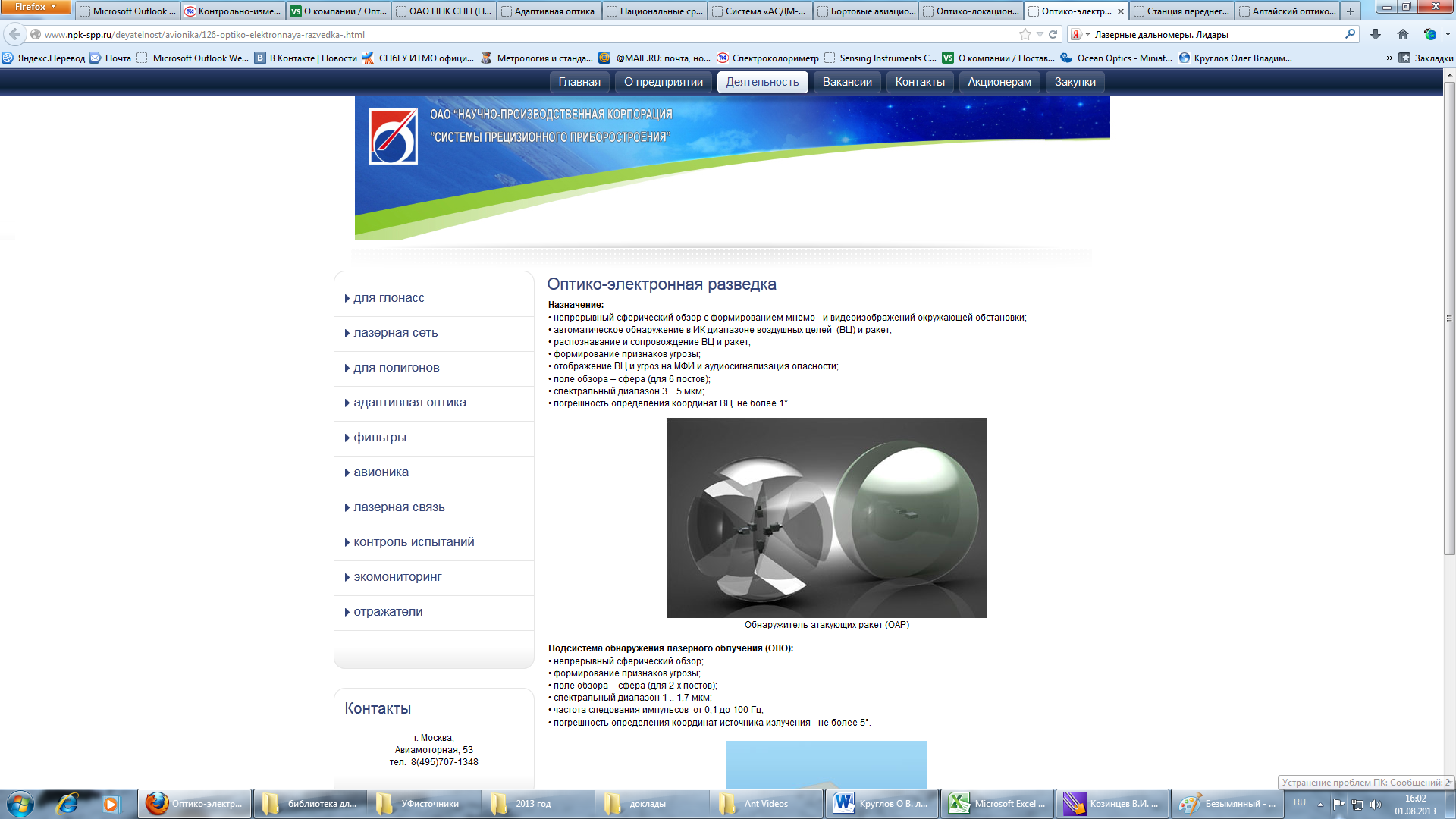
Рисунок 139. Обнаружитель атакующих ракет (ОАР), Оптико-локационная станция ОЛС-35
Рисунок 140. Средство национального технического контроля испытаний стратегического вооружения в соответствии с международными Договорами.
4.8 Интерферометры
Интерферометры - это измерительные приборы, действие которых основано на явлении интерференции.
Работа приборов построена на последовательном разложение пучка излучения ( на два или большее количество когерентных пучков каждый из них проходит различные оптические пути) и последующим их сложением, в результате создаётся интерференционная картина, по которой можно установить смещение фаз пучков.
С помощью интерферометров производится измерение угловых размеров звезд и угловых расстояний между звездами, измерение показателей преломления газов и жидкостей, а также определение концентрации примесей в воздухе. Интерферометры используются для контроля качества оптических деталей и их поверхностей, для контроля чистоты обработки металлических поверхностей.
Так как в основе принципа работы интерферометров лежит явление интерференции света, начнём изучение данной группы приборов с изучения этого явления.
Интерференции света — перераспределение интенсивности света в результате наложения (суперпозиции) нескольких световых волн. Это явление сопровождается чередующимися в пространстве максимумами и минимумами интенсивности. Её распределение называется интерференционной картиной.
Впервые явление интерференции было независимо обнаружено Робертом Бойлем (1627—1691 гг.) и Робертом Гуком (1635—1703 гг.). Они наблюдали возникновение разноцветной окраски тонких плёнок (интерференционных полос), подобных масляным или бензиновым пятнам на поверхности воды. В 1801 году Томас Юнг (1773—1829 гг.), введя «Принцип суперпозиции», первым объяснил явление интерференции света, ввел термин «интерференция» (1803). Он также выполнил первый демонстрационный эксперимент по наблюдению интерференции света, получив интерференцию от двух щелевых источников света (1802); позднее этот опыт Юнга стал классическим .
Рисунок 141. Опыт Юнга и Интерференция в тонкой плёнке.
Ещё один метод получения устойчивой интерференционной картины для света служит использование воздушных прослоек, основанное на одинаковой разности хода двух частей волны: одной — сразу отраженной от внутренней поверхности линзы и другой — прошедшей воздушную прослойку под ней и лишь затем отразившейся. Её можно получить, если положить плосковыпуклую линзу на стеклянную пластину выпуклостью вниз. При освещении линзы сверху монохроматическим светом образуется тёмное пятно в месте достаточно плотного соприкосновения линзы и пластинки, окружённое чередующимися тёмными и светлыми концентрическими кольцами разной интенсивности. Тёмные кольца соответствуют интерференционным минимумам, а светлые — максимумам, одновременно тёмные и светлые кольца являются изолиниями равной толщины воздушной прослойки. Измерив радиус светлого или тёмного кольца и определив его порядковый номер от центра, можно определить длину волны монохроматического света. Чем круче поверхность линзы, особенно ближе к краям, тем меньше расстояние между соседними светлыми или тёмными кольцами. Данная методика используется для контроля оптических деталей.
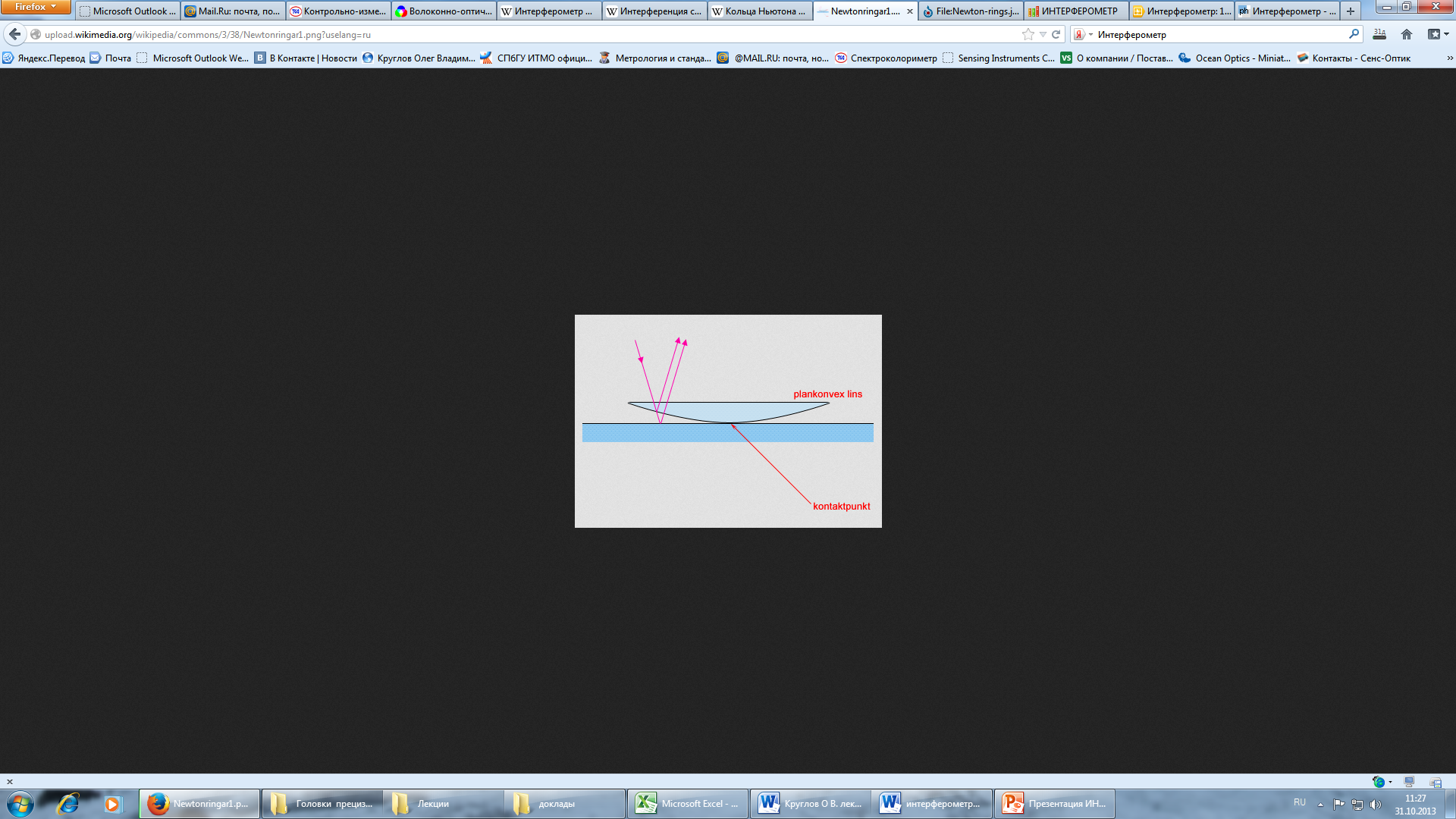
Рисунок 142. Кольца Ньютона
Разобрав явление интерференции, перейдём к рассмотрению схем построения интерферометров.
Интерферометр Майкельсона является одной из наиболее распространенных скелетных схем интерферометра, предназначенной для различных применений в случае, когда пространственное совмещение объектов, порождающих интерферирующие волны, невозможно или в силу каких-то причин нежелательно.
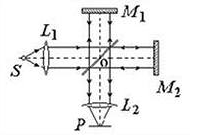
Рисунок 143. Интерферометр Майкельсона
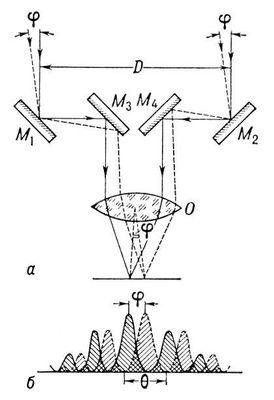
Звездный интерферометр Майкельсона— интерферометр для измерения угловых размеров звёзд и углового расстояний между двойными звёздами. Если угловое расстояние между двумя звездами очень мало, в телескоп они видны как одна звезда. В таком случае говорят о двойных звездах и надо провести специальное наблюдение, чтобы отличить их от звезд одиночных. Для этого используется звездный интерферометр Майкельсона, который позволяет к тому же определить угловое расстояние между звездами.
Рисунок 143.Звёздный интерферометр Майкельсона
Лучи света, пришедшего от удаленной звезды, отражается от плоских зеркал M1 — M2, разнесенных на достаточно большое расстояние D, затем отражаются от двух других зеркал и собираются линзой на экране, помещенном в фокальной плоскости. Разнесенные на расстояние D зеркала можно рассматривать как точечные источники, расстояние между которыми и равно D. Вследствие этого в изображении звезды наблюдается интерференционная картина, аналогичная интерференции от двух щелей, расположенных на расстоянии D друг от друга. Угловое расстояние между соседними интерференционными максимумами в этой картине равно θ=λ/D, где λ – длина волны света. При наличии двух близких звёзд, находящихся на малом угловом расстоянии φ друг от друга, в телескопе образуются 2 интерференционные картины, которые также смещены на угол φ и накладываются друг на друга. В зависимости от соотношения углов θ и φ видимость полос суммарной картины будет различной. Изменяя расстояние D и, следовательно, изменяя угол θ, можно добиться совмещения максимумов одной интерференционной картины с минимумами другой, в результате чего видимость полос будет наихудшей. При этих условиях φ=½θ=λ/2D. Измерив D и зная λ, можно определить угловое расстояние между звёздами φ. Аналогично определяются угловые размеры одной звезды. Если звезду рассматривать как равномерно светящийся диск, то расчёт показывает, что исчезновение полос происходит при φ=1.22λ/D. Точность измерения звёздного интерферометра тем больше, чем больше база D. Построен звездный интерферометр, в котором D может достигать 18 м. что позволяет измерять угловое расстояние с точностью до 0,001". Для измерения угловых размеров очень слабых звёзд, свет от которых на уровне шумов, применяют метод корреляции интенсивностей.
И
нтерферометр
Рождественского
– это двухлучевой интерферометр,
состоящий из 2-х зеркал M1 , M2 и двух
параллельных полупрозрачных пластин
P1 , P2; M1, P1 и M2, P2 устанавливаются попарно
параллельно, но М1 и М2 наклонены
относительно друг друга на малый угол;
расстояние М1Р1 = М2Р2 и M1P2=P1M2. Луч света
разделяется пластиной Р1 на 2 луча,
которые после отражений от M1 , M2 и
прохождения Р2 оказываются параллельными
с разностью фаз
δ = (4πD/λ)(cos i1 — cos i2).
Рисунок 144. Интерферометр Рождественского
Поскольку δ не зависит от положения лучей на зеркалах и определяется лишь углами падения, интерференционная картина будет локализована на бесконечности (или в фокальной плоскости объектива О). Параллельному пучку лучей, падающих на Интерферометр Рождественского, соответствует одна точка интерференционно картины, и, следовательно, для наблюдения всей картины необходим пучок конечной апертуры. Вид картины (порядок и ширина полос, их ориентация) зависит от наклона зеркал M1 и M2. Если, например, ребро двугранного угла, образованного M1 и M2, вертикально (перпендикулярно чертежу), то даже при очень малой разности (i1-i2) полосы сравнительно высокого порядка (D велико) вертикальны и почти параллельны.Если же ребро двугранного угла горизонтально, то в поле зрении находятся горизонтальные полосы низкого порядка (в т.ч. нулевая), видные и в белом свете. Введение в один из пучков к.-л. прозрачного объекта, например пластинки, изменяет ширину, порядок и ориентацию полос: нулевая полоса не горизонтальна и появляется при некоторой промежуточной ориентации M1 и M2 ; при очень большой толщине этой пластинки в белом свете можно видеть только очень узкие, почти вертикальные полосы, когда ребро угла между M1 и M2 почти вертикально. Ширина полос зависит от угла между M1 и Р1, увеличиваясь с его уменьшением. Если все зеркала и пластины параллельны, то в отсутствие неоднородностей ширина полос бесконечна (интерференционное поле равномерно освещено).
Интерферометр Жамена (интерференционный рефрактометр) — интерферометр для измерения показателей преломления газов и жидкостей, а также для определения концентрации примесей в воздухе.
Интерферометр Жамена состоит из двух одинаковых толстых плоскопараллельных пластинок из стекла(или кварца), установленных почти параллельно друг другу. Пучок света падает на первую пластинку под углом i, близким к 45°. Каждый луч пучка после отражения на поверхностях пластинки делится на 2 когерентных луча S1 и S2 , идущих на некотором расстоянии друг от друга, зависящем от толщины пластинок d. Далее на второй пластинке каждый из них аналогичным образом разделяется на два луча. В результате от второй пластинки идут 4 параллельных когерентных луча S1’, S1”, S2’, S2”; Средние пучки S1” И S2’ налагаются и образуют интерференционную картину в фокальной плоскости объектива О1.
Рисунок 145. Схема интерферометра Жамена: ОО – ось вращения компенсаторных пластинок; L – лимб поворота компенсатора; О1 и О2 – объектив и окуляр зрительной трубы.
Разность хода между ними равна
,
где nп — показатель преломления пластинок.
φ — угол междуними.
При (φ ≈ 5′ - 15′ ∆ мала, поэтому при использовании источника белого света наблюдаются только интерференционные полосы низкою порядка, которые имеют форму прямых линий с белой ахроматической полосой в центре, окружённой системой окрашенных полос.).
Сравнительно большое расстояние между лучами S1 и S2 , позволяет установить на их пути две кюветы К1 и К2 одинаковой длины l с исследуемыми веществами, показатели преломления которых n1 и п2. Возникающая разность хода , что вызовет смещение интерференционной картины.
∆ = (n2—n1)l = δnl
С помощью Интерферометра Жамена проводят количественный анализ газовых смесей — определяют концентрацию некоторых газообразных примесей, например метана и СО2 , в воздухе шахт (т. к. n зависит от природы газа).
Интерферометр Физо- один из простейших интерферометров применяемый главным образом для контроля точности изготовления плоских поверхностей оптич. деталей.
Свет от монохроматического источника L с помощью конденсора O1 диафрагмы D и объектива О2 направляется параллельным пучком на эталонную Э и контролируемую К пластинки (положенные одна на другую) почти перпендикулярно к их поверхностям. При этом строго плоская эталонная и контролируемая поверхности пластинок образуют между собой небольшой угол a. С помощью полупрозрачной пластинки П в отражённом свете наблюдаются интерференционные полосы равной толщины ,которыерые локализованы в области воздушного клина между контролируемой и эталонной поверхностями.
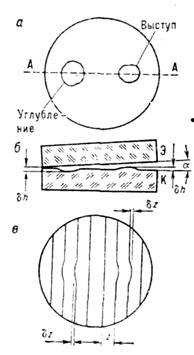
Рисунок 146. Интерферометр Физо; а - Вид дефектов сверху на контролируемой пластинке; б - Сечение эталонной и контрольной пластинок. Сечение по линии А-А (угол a и размеры дефектов для наглядности сильно увеличены); в - Вид интерференционной картины полос равной толщины в интерферометре Физо.
Положения этих полос определяются из условия: D=2dn+l/2=ml=const (при п~1), где d - толщина воздушного клина. Если контролируемая поверхность идеально плоская, то полосы равного наклона имеют форму прямых эквидистантных линий, параллельных ребру клина (d=const), расстояние между к-рыми равно z=l/2a (рис. 2, в) (при a=10'' и l~0,5 мкм, z=5 мм). Если же на контролируемой поверхности имеются к--л. дефекты, например, небольшие углубления или выступы, как на рисунке или она не строго плоская, то в области расположения этих дефектов наблюдаются отклонения dz от прямолинейности. При этом относит, величина отклонения dz/z связана с высотой или глубиной дефекта dh соотношением dh=(l/2)dz/z.
Невооружённый глаз может оценить величину dz/z~0,l, что соответствует величине обнаруженного дефекта dh=l/20 (при l=0,633 мкм, dh=0,031 мкм). Знак отклонения позволяет отличить тип дефекта: углубление или выступ. Если контролируемая поверхность имеет форму сферы, то интерференционные полосы имеют форму концентрических окружностей (см. Ньютона кольца). В интерферометре Физо поверхности контролируемой и эталонной пластинок из-за малости угла (угл. секунды) почти полностью соприкасаются друг с другом и в процессе юстировки могут быть повреждены. Поэтому для контроля поверхностей часто используются бесконтактные интерферометры, построенные по схеме интерферометра Майкельсона.
Рисунок 147. Интерферометр Физо конструкции Романова предназначен для бесконтактного измерения формы плоских полированных поверхностей и зеркал. Программное обеспечение предназначено для обработки интерференционных картин с дополнительно введёнными наклонами.
Литература.
Д. Н. Черкасова, А. В. Бахолдин / «Оптические офтальмологические приборы и системы Часть I»/ Санкт-Петербург 2010.
Лукин С.Б. / «КОНСПЕКТ ЛЕКЦИЙ ПО КУРСУ ОЭС» / СПбГУ ИТМО 2004г.
Латыев С.М./ « Конструирование точных (оптических) приборов»/ Электронный учебник по дисциплине: "Основы конструирования оптических приборов". СПбГУ ИТМО
А.Л. Андреев / «Автоматизированные телевизионные системы наблюдения» / СПбГУ ИТМО
Митрофанов С.С / «Теоретические и физические основы устройства ОП»/ Электронный учебник по дисциплине: "Прикладная оптика". СПбГУ ИТМО, кафедра КиПОП
http://biggest.su/samyj-bolshoj-teleskop/
В. Самохин, Н. Терехова/ «Видеопроекция сегодня и завтра»
М.А. Кустикова, М.Н. Мешалкина, В.Л. Мусяков, А.Н. Тимофеев/ «Методические указания к лабораторным работам по разделу «ОПТИКО-ЭЛЕКТРОННЫЕ ГАЗОАНАЛИЗАТОРЫ» курса «ЭКОЛОГИЧЕСКИЙ МОНИТОРИНГ»
.Майкельсон А.А. Исследования по оптике. М. – Л., 1928
http://www.krugosvet.ru/enc/nauka_i_tehnika/fizika/OPTIKA.html?page=4,6
.Захарьевский А.Н. «Интерферометры» 1952.
М.М. Мирошников / «Теоретические основы ОЭП»/ «Машиностроение « 1977г.
М.М. Русинов / «Габаритные расчёты оптических систем» Москва 1963
Г.Г. Ишанин, М. Г. Козлов, К.А. Томский / «Основы светотехники»/ СПб 2004г