19

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ

Утверждено

на заседании кафедры

высшей геодезии и фотограмметрии

___________________ г.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

для выполнения курсового проекта на тему

«Прецизионный метод фотограмметрического сгущения»

для студентов III курса специальности

«Прикладная геодезия»

Ростов-на-Дону, 2008

Методические указания для выполнения курсового проекта на тему «Прецизионный метод фотограмметрического сгущения» для студентов III курса специальности - «Прикладная геодезия». – Ростов-на-Дону: Рост. гос. строит. ун-т, 2008. – 24 с.

В методических указаниях изложены вопросу по решению задачи фотограмметрического сгущения сети аналитическим способом.

Составители: к.э.н., доц. Самсонова Н.В.

асс. Говорухин М.Г.

Рецензенты: д.т.н., проф. Куштин И.Ф.

к.т.н., доц. Лысков Г.А.

© Ростовский государственный

строительный университет, 2008

Цель методических указаний – ознакомить студентов с порядком построения сети пространственной фототриангуляции и методикой аналитической обработки при сгущении фотограмметрической сети.

Содержание курсового проекта:

Введение

1. Составление проекта фототриангуляции

2. Измерение снимков на стереоприборе

3. Математическое обоснование процессов внутреннего и взаимного ориентирования снимков

4. Вычисление координат точек модели и ее внешнее ориентирование

5. Представление полученных результатов с комментариями о соответствии их требованиям точности

6. Построение и уравнивание сети пространственной фототриангуляции

Сущность и основные процессы маршрутной фототриангуляции

Пространственной фототриангуляцией называют метод камерального сгущения съемочного обоснования путем построения и уравнивания фотограмметрической сети. Координаты точек, получаемые в результате уравнивания сети, используются для составления топографических карт, планов, фотопланов и иных документов. Основной целью пространственной фототриангуляции является максимальное сокращение объема полевых геодезических работ.

С ущность метода заключается в следующем.

Пусть из точек S₁, S₂, S₃, S₄ (рис. 1) получены снимки Р₁, Р₂, Р₃, Р₄. Установим эти снимки в то положение, которое они занимали в момент фотографирования. Эта система характеризуется следующими признаками.

1. Все проектирующие лучи проходят через центры фотографирования и точки аэроснимков. Значит, связки внутренне ориентированы.

2. Пары соответственных проектирующих лучей S₁21 и S₂21, S₁01 и S₂01, S₂22­ и S₃22 и др., пересекаются в точках 01, 02, …, 24, т.е. все они компланарны и лежат в базисных плоскостях. Следовательно, пары снимков взаимно ориентированы.

3. Тройки проектирующих лучей S₁02, S₂02 и S₃02; S₁12, S₂12 и S₃12 и др. пересекаются в точках 02, 12, 22, …, 04, 14, 24. Значит, построенные по стереопарам Р₁ и Р₂, Р₂ и Р₃, Р₃ и Р₄ и др. фотограмметрические модели имеют единый масштаб и представляют единую модель маршрута в свободной системе координат, т.е. маршрутная сеть построена только по фотограмметрическим данным.

4. П роектирующие лучи S₁01, S₁21, S₄04 и S₄24 проходят через опорные точки 01, 21, 04 и 24. Значит, фотограмметрическая система координат совмещена с геодезической, и маршрутная сеть ориентирована по опорным точкам.

Обычно центры фотографирования и точки модели, полученные из этих центров прямыми фотограмметрическими засечками, называют звеньями фототриангуляции и обозначают номерами центров фотографирования.

Таким образом, для построения фототриангуляционной сети нужно выполнить следующие операции:

• внутреннее ориентирование снимков;

• взаимное ориентирование снимков исходя из условия компланарности соответственных векторов;

• определение фотограмметрических координат точек модели (построение начального звена);

• построение следующего звена (взаимное ориентирование, определение фотограмметрических координат точек) и объединение его с предыдущим по точкам связи в зоне тройного продольного перекрытия;

• внешнее (геодезическое) ориентирование маршрутной сети по опорным точкам и перевычисление фотограмметрических координат точек в систему местности.

Одиночная модель образуется как совокупность точек, координаты которых получаются по координатам соответственных точек стереопары

(1)

где X, Y, Z – координаты точки местности в системе координат XYZ с началом в левой точке фотографирования (рис. 2);

X’₁, Y’₁, Z’₁ – координаты точки левого снимка в той же системе координат.

Множитель N зависит от составляющих базиса фотографирования B_X и B_Z, а также от пространственных координат точки левого снимка (в системе S₁XYZ) и соответственной точки правого снимка (в системе S₂XYZ, параллельной S₁XYZ)

(2)

Пространственные координаты точки снимка связаны с плоскими координатами х и у зависимостями

(3)

где a, b, c – направляющие косинусы углов, образованных координатными осями x, y, z с осями X, Y, Z (табл. 1);

х₀, у₀ – координаты главной точки снимка.

Координата z для всех точек снимка постоянна и равна –f­.

Таблица 1

Оси	x	y	z
X	a1	a2	a3
Y	b1	b2	b3
Z	c1	c2	c3

Н аправляющие косинусы зависят от угловых элементов внешнего ориентирования снимка , ,  (рис. 3)

(4)

Эти косинусы связаны между собой шестью независимыми уравнениями

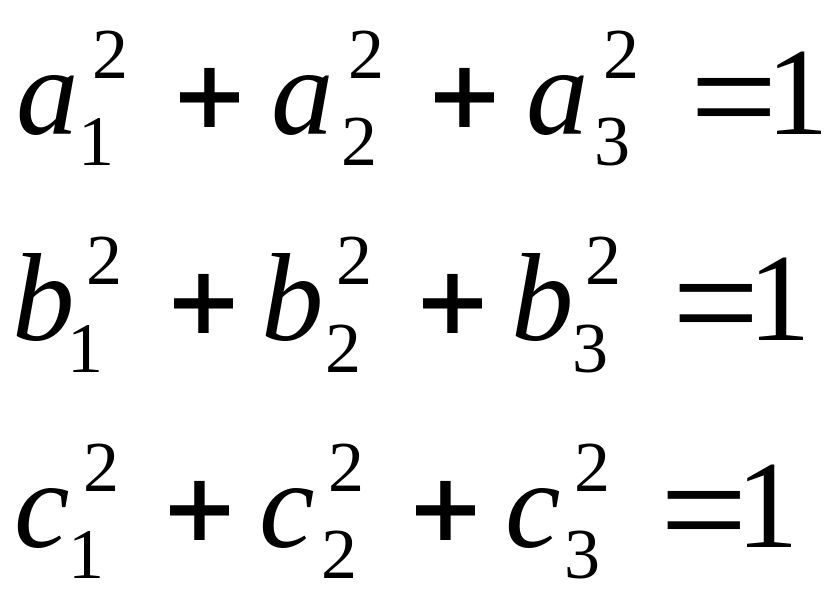
(5)

Следовательно, из девяти косинусов независимых только три.

Если направляющие косинусы известны, то угловые элементы внешнего ориентирования снимка можно найти по формулам

(6)

Таким образом, для определения координат точки местности необходимо измерить координаты х и у ее изображений на паре снимков и знать их элементы внутреннего и внешнего ориентирования. При этом в измеренные координаты точек стереопары вводят поправки, чтобы исключить влияние деформации снимков, дисторсии объектива съемочной камеры, атмосферной рефракции, кривизны Земли и других систематических ошибок.

Процесс соединения отдельных моделей в общую модель часто называется взаимным ориентированием моделей. Он выражается формулами преобразования прямоугольных координат

(7)

где X_F, Y_F, Z_F – координаты точки фототриангуляции в общей для всех моделей системе X_FY_FZ_F;

X₀, Y₀, Z₀ – координаты начала системы координат XYZ отдельной модели;

X, Y, Z – координаты точки фототриангуляции в системе XYZ;

a_i’, b_i’, c_i’ – направляющие косинусы углов, образованных осями X, Y, Z с осями X_F, Y_F, Z_F;

t – знаменатель масштаба отдельной модели;

t₀ – знаменатель масштаба общей модели.

Величины X₀, Y₀, Z₀ в формулах (7) являются координатами точки фотографирования левого снимка стереопары – X_S, Y_S, Z_S.

Взаимное ориентирование моделей выполняется по связующим точкам, выбираемым в зоне тройного перекрытия снимков.

Система координат X_FY_FZ_F, общая для всех моделей, обычно занимает произвольное положение относительно геодезической системы координат. Поэтому возникает необходимость внешнего ориентирования модели.

Внешнее ориентирование модели производится при помощи плановых и высотных опорных точек. В процессе внешнего ориентирования фотограмметрической сети учитывается и ее деформация, возникающая вследствие ошибок построения отдельных моделей и их соединения.

В данном способе маршрутной фототриангуляции в качестве начала общей системы координат X_FY_FZ_F принимается точка фотографирования первого снимка маршрута. Координатные оси X_F и Y_F устанавливаются в соответствии с угловыми элементами внешнего ориентирования первого снимка α, ω, κ.

Угловые элементы внешнего ориентирования правого снимка первой стереопары находят по углам , ,  левого снимка и элементам взаимного ориентирования этой пары.

Перед вычислением фотограмметрических координат точек первой модели измеренные координаты х и у точек первой стереопары трансформируют по формулам

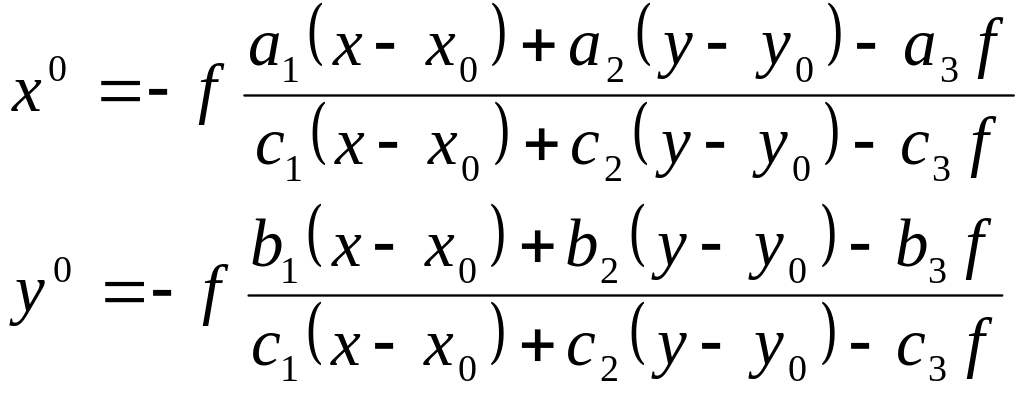
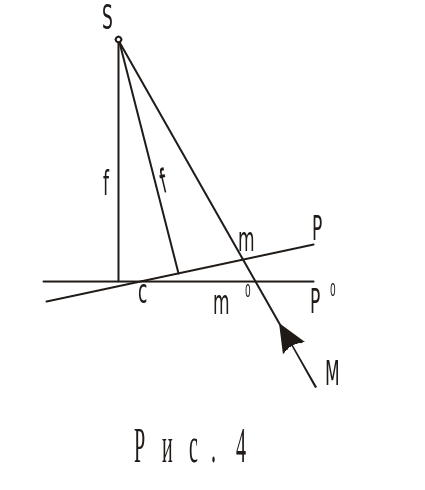. (8)

При этом направляющие косинусы находят по формулам (4) для левого и правого снимков. Полученные таким образом координаты и , а также и относятся к новым снимкам, параллельным плоскости X_FY_F. Однако фокусное расстояние этих снимков не изменяется по сравнению с наклонными снимками (рис. 4).

В связи с этим формулы (1) и (2) для вычисления координат точек местности примут вид

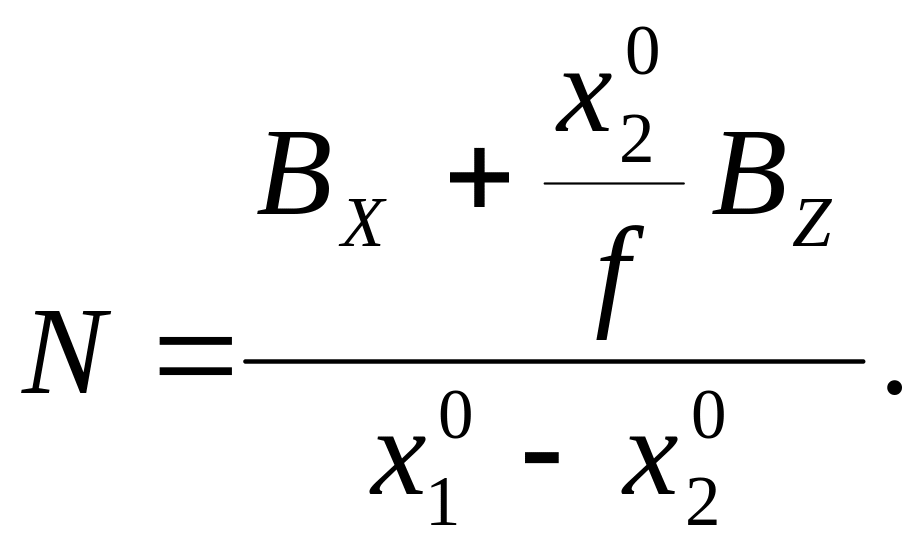(9)

Для построения второй модели в качестве элементов внешнего ориентирования левого снимка второй стереопары берут величины, полученные при построении первой модели для правого снимка первой стереопары. Таким образом, система координат второй модели параллельна системе координат первой модели.

В остальном построение второй и последующих моделей не отличается от построения первой модели.

Соединение последующей модели с предыдущей в данном случае состоит лишь в масштабном преобразовании, т.е. в приведении последующей модели к масштабу предыдущей и в переносе начала координат

(10)

где t : t₀ =  – масштабный коэффициент.

Координаты точек фотографирования, необходимые для соединения отдельных моделей в общую модель, находят по составляющим базисов фотографирования

(11)

Здесь индекс k обозначает номер точки фотографирования и номер снимка, принимая значения от нуля до n. При такой нумерации снимков и точек фотографирования номер базиса и номер модели совпадают с номером точки фотографирования правого снимка стереопары.

Таким образом, основными процессами аналитического способа маршрутной фототриангуляции являются: