Лекция 4. Интегрирование дифференциальных уравнений невозмущенных движений исз. Интеграл площадей.

Система дифференциальных уравнений (2) является системой 6ого порядка, поэтому должны существовать 6 независимых интегралов, полностью определяющих движение спутника, т.е. вид и форму орбиты; ее положение в пространстве и закон движения по ней. Каждый интеграл содержит одну произвольную постоянную, поэтому 6 произвольных постоянных полностью определяют невозмущенное движение ИСЗ.

Интегрируя (2) методом разделения переменных, получим:

Три интеграла площадей; интеграл энергии; интеграл орбиты и динамический интеграл.

Интеграл площадей.

Запишем дифференциальные уравнения невозмущенного движения: Умножим по схеме и сложим, тогда:

-y	+z
+x		-z
	-x	+y

В каждом из полученных уравнений заменим одну производную через дифференциал, тогда получим:

интегрируя эту систему найдем:

умножим по схеме, сложим

и получим:

(3)

Это значит, что невозмущенная орбита ИСЗ лежит в плоскости, проходящей через центр масс Земли и называется орбитальной плоскостью.

Если в орбитальной плоскости выбрать произвольную систему плоских прямоугольных координат ξ и η, то по аналогам с пространственной системой по осям ξ и η, получим:

ξ умножим по схеме, сложим

-η и найдем:

Заменим одну производную через

дифференциал, тогда:

после интегрирования найдем:

(4)

В данной плоской системе координат рассмотрим возможность определения и через полярные координаты и φ, тогда ,

Дифференцируя, найдем: ; (5)

Подставляя (5) в (4) получим:

Откуда:

или

(6)

Если в этом уравнении взять производную по времени, то получим удвоенную секториальную скорость, т.е. удвоенную площадь, описываемую радиус-вектором τ в единицу времени.

Таким образом, секториальная скорость есть величина постоянная и тем самым строго доказан второй закон Кеплера. Поэтому первые 3 интеграла называются интегралами площадей.

Лекция 5. Элементы орбиты исз.

При решении практических задач, связанных с использованием ИСЗ, требуется знать положение спутника в пространстве в произвольный момент времени. Для этого, из решения 3х дифференциальных уравнений второго порядка, необходимо найти x,y,z-искомые координаты спутника, которые выражаются функциями от независимого переменного t и 6ти произвольных постоянных (параметров орбиты).

В связи с этим, рассмотрим движение спутника по эллиптической орбите, т.е. установим 6 параметров, из которых 5 определяют пространственное положение орбиты, а 6ой определяет мгновенное положение ИСЗ в пространстве и является функцией времени.

Для этого построим эллиптическую орбиту так, чтобы один из фокусов эллипса совпадал с точкой О (центр масс Земли).

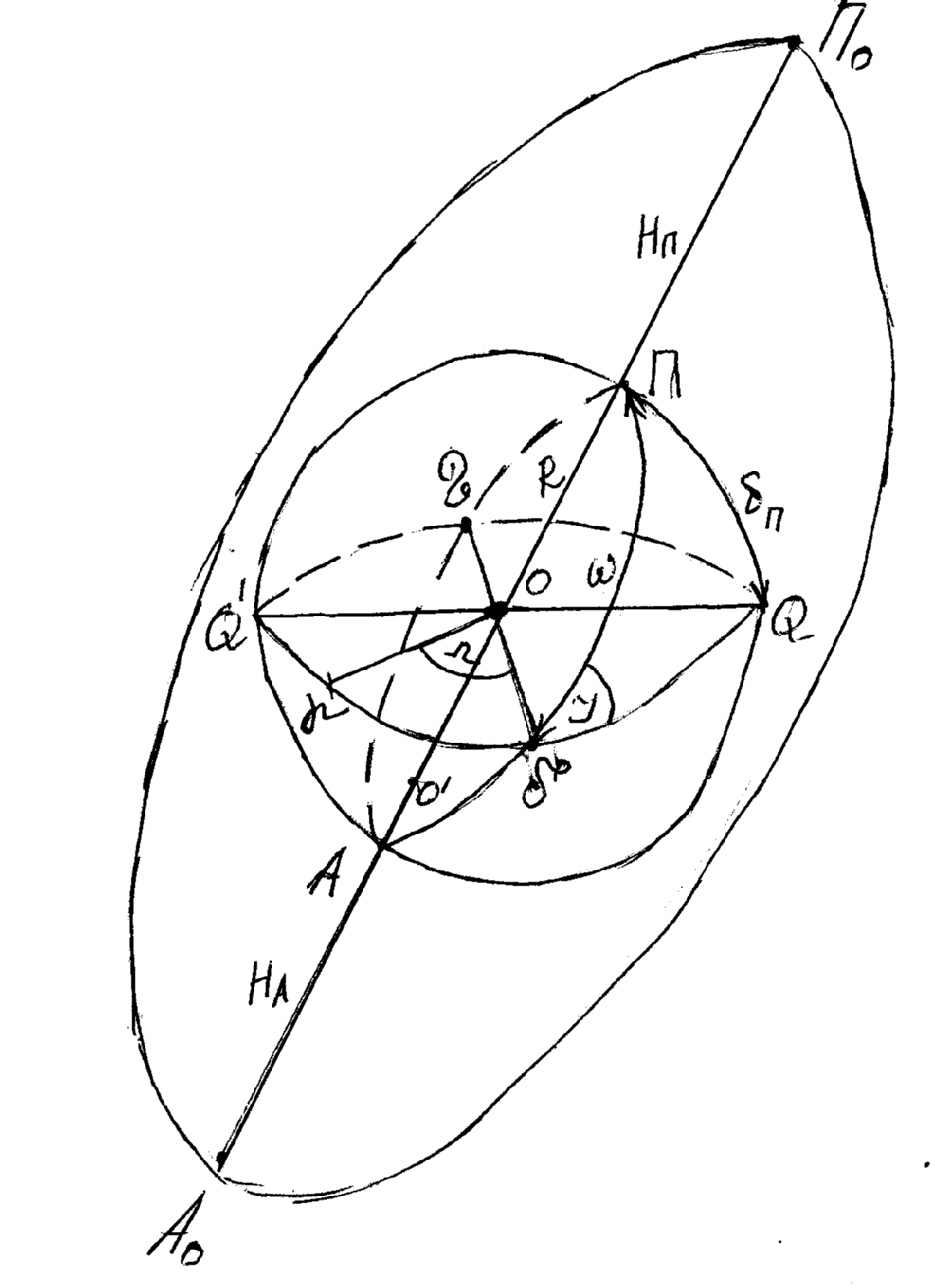
R-радиус сферы (ср.радиус Земли)

О’- центр эллиптической орбиты

П₀-перигей, А₀-апогей

П- перицентр (проекция П₀ на сферу),А-Апоцентр

QQ’-экватор,

-Восходящий узел орбиты

-Нисходящий узел орбиты

- Линия узлов

АП-линия АПСИД, OO’=c=a-ea=a(1-e)

Элементы орбиты:

1. Наклонение орбиты J-угол между плоскостью орбиты и плоскостью экватора;

2. Долгота восходящего узла- угол в плоскости экватора от направления в точку весеннего равноденствия (γ ) до линии узлов.

Эти 2 параметра определяют положение орбиты ИСЗ в пространстве.

3. Большая полуось а орбиты- определяет размер орбиты.

4. Эксцентриситет е орбиты – определяет форму орбиты

5. Склонение перицентра δ_п (дуга сферы ПQ) или аргумент перигея ω (угол в плоскости орбиты от линии узлов до линии АПСИД). Параметр δ_п (ω) определяет расположение (ориентирование) эллипса в плоскости орбиты.

6. Момент прохождения ИСЗ через перигей или узел орбиты- t₀

Из чертежа следует:

ОП₀=R+ H_п =a-c=a-ae=a(1-e)

OA₀= R+H_a= a+c=a+ae=a(1+e), откуда

H_п=a(1-e)-R

H_a=a(1+e)-R (1)

Если в системе (1) сложить правые и левые части, то получим:

H_a + H_п=2а-2R; (2)

Если в системе (1) не сложить, а вычесть, то найдем:

H_a + H_п=2ае; (3)