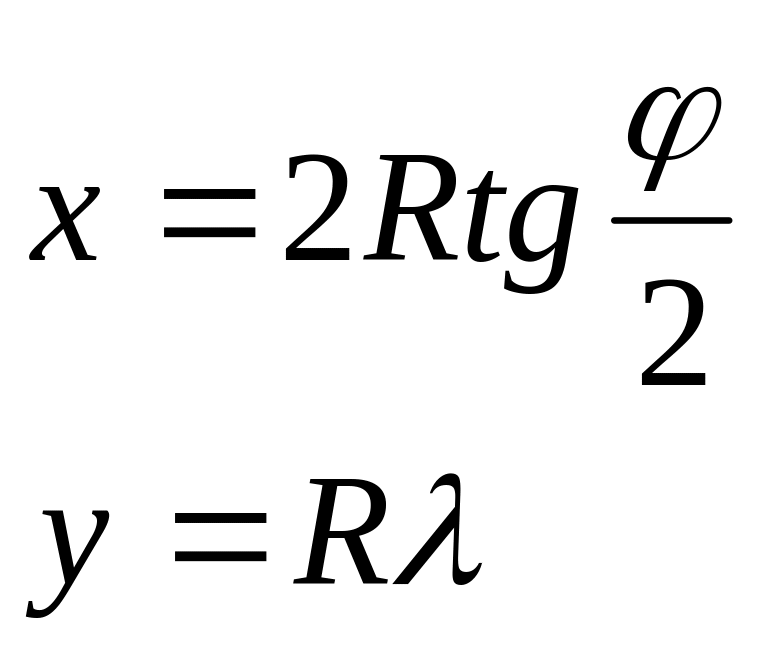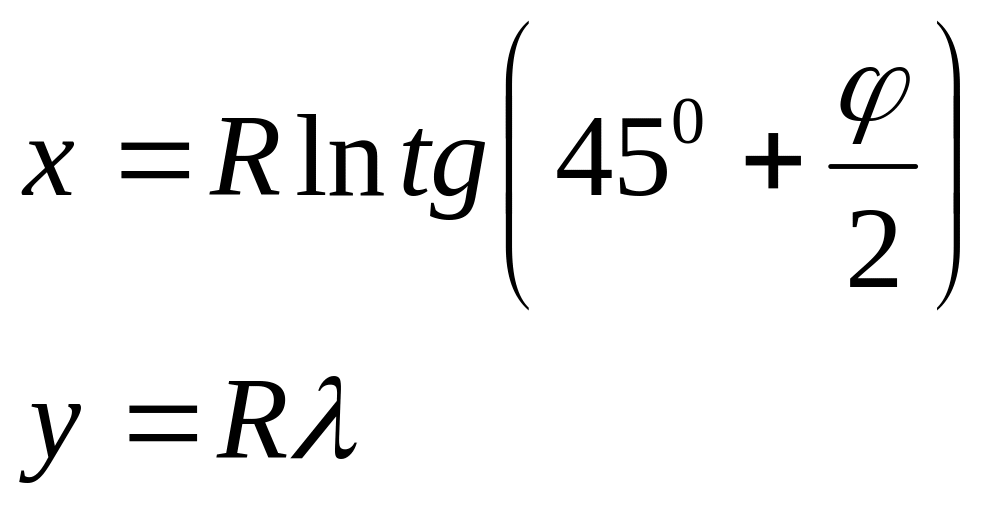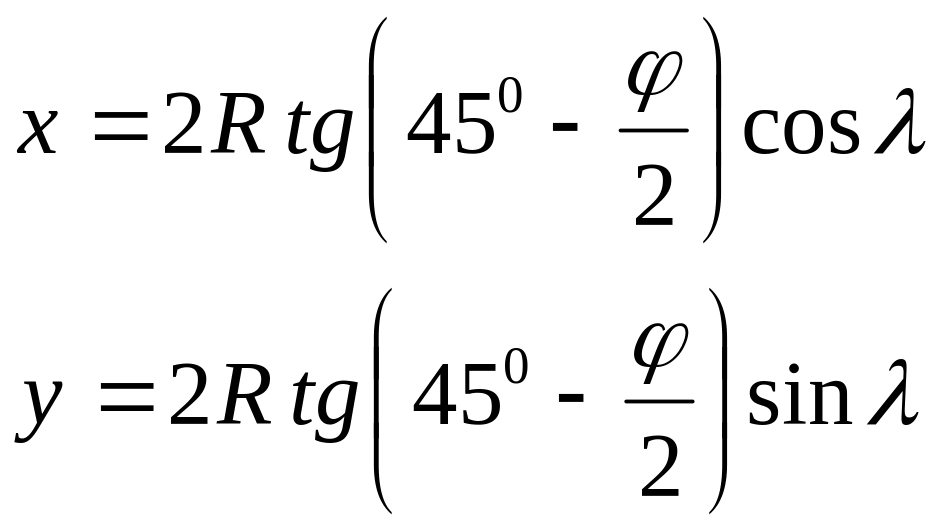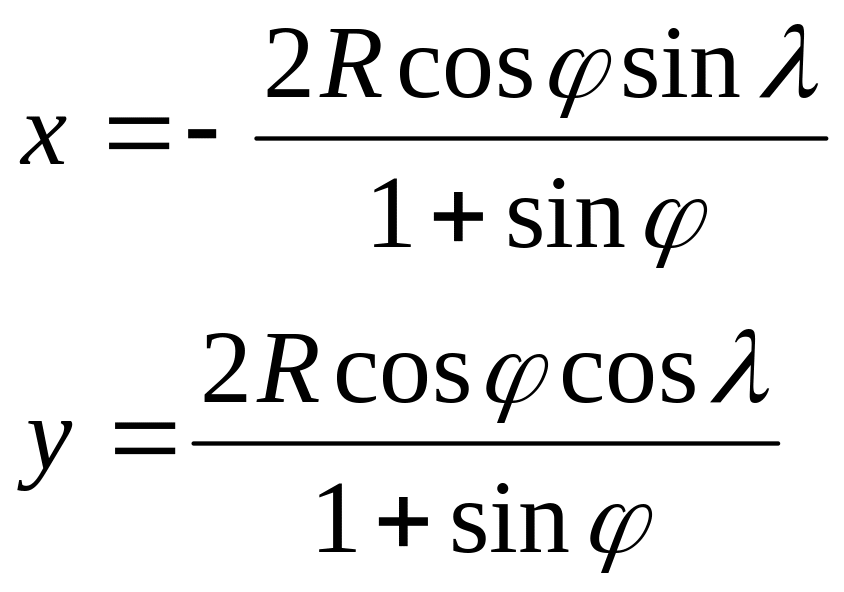33

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ

Утверждено

на заседании кафедры

высшей геодезии и фотограмметрии

4 Ноября 2004 г.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

по курсу «Общая картография»

(для студентов 5 курса специальности 3001 – Прикладная геодезия)

Ростов – на – Дону 2004

УДК 528.7 075.8

Методические указания к лабораторным работам по курсу «Общая картография» для студентов 5 курса специальности «Прикладная геодезия». –

Ростов – на – Дону: Рост. гос. строит. ун-т, 2004. – 33 с.

Методические указания состоят из двух частей. Впервой части дается порядок выполнения лабораторной работы по разделу математической картографии, приведены примеры расчета, варианты индивидуальных заданий.

Во второй части приведена технология создания топографических карт методом составления (камеральным методом), даны рекомендации по разработке редакционно-технических указаний и составлению оригинала карты в масштабе 1:10 000; 1:25 000; 1:50 000 и 1:100 000.

Приведены требования к оформлению составительского оригинала карты.

Составители: к.т.н., доц. Л.Г. Долина

ассист. Н.А. Калачева

Рецензент: доц. В.Г. Кривоногов

 Ростовский государственный

строительный университет, 2004

ВВЕДЕНИЕ

Методические указания составлены в соответствии с программой курса «Общей картографии» для высших учебных заведений по специальности 3001 – Прикладная геодезия, утверждены кафедрой Высшей геодезии и фотограмметрии.

Содержат задания и указания о порядке выполнения лабораторных работ.

Разработаны с учетом возросших требований к качеству подготовки специалистов – инженеров широкого профиля.

Выполнение заданий основано на использовании знаний, полученных по математике, сферической тригонометрии, высшей геодезии др.

При выполнении работ следует пользоваться картографическими таблицами, помещенными в приложениях к рекомендуемой литературе.

ЦЕЛЬ ЗАДАНИЯ

1. Закрепление теоретических знаний по разделу математическая картография.

2. Приобретение практических навыков по анализу картографических проекций, их расчету и построению.

3. Подготовка к созданию карты камеральным методом. Составление формуляра карты.

4. Построение математической основы. Перенос изображения, генерализация.

5. Оформление составительского оригинала.

ЧАСТЬ ПЕРВАЯ

Задачи и примеры по общей теории отображения картографируемой поверхности на плоскости

В математической картографии картографируемые поверхности обычно принимают за сферу радиуса R или за эллипсоид вращения, малая ось которого совпадает с осью вращения Земли.

При создании карт, т.е. при изображении сферической поверхности на плоскости, происходят искажения длин, углов и площадей. Поэтому перенос изображения со сферы на плоскость производят по определенным математическим законам, выражающим функциональную связь координат точек картографируемой поверхности и плоскости. Такие способы переноса изображения носят название картографических проекций.

В основы отображения картографируемой поверхности положена система координат, координатными линиями которых являются меридианы и параллели.

Меридианы и параллели на земной поверхности или глобусе образуют систему линий, называемую географической сеткой, а ее изображение на карте (в проекции) называют картографической сеткой.

Положение меридианов и параллелей на картографируемой поверхности определяется криволинейными географическими координатами: долготой  и широтой . В проекции им соответствуют прямоугольные координаты Y и X.

Общие уравнения картографических проекций:

; , (1)

где  и  - географические координаты некоторой точки на картографируемой поверхности;

X и Y – прямоугольные координаты изображения этой точки на плоскости в проекции, определяемой функциями f₁ и f₂.

Уравнения меридианов и параллелей имеют вид:

; .

Следовательно, для получения уравнений меридианов и параллелей в проекции надо из формул (1) поочередно исключить широту и долготу.

Если проекция описывается уравнениями и , то картографическая сетка будет иметь наиболее простой вид – две системы взаимно перпендикулярных прямых линий.

Если и , то параллели изобразятся прямыми линиями, параллельными оси Y, а меридианы - кривыми.

Если и , то меридианы будут прямыми, параллельными оси X, а параллели - кривыми.

Если и , то параллели и меридианы будут кривыми линиями. Это могут быть окружности, эллипсы, параболы, синусоиды или линии любой кривизны.

Исключение широты и долготы из уравнений вида (1) производится совместным решением заданных уравнений, используя различные математические действия, например, деление одного уравнения на другое, возведение в степень и суммирование соответствующих частей уравнений и т.п. Основными критериями, определяющими достоинство картографических проекций, являются величины масштабов по меридианам (m) и параллелям (n) и площади (p), ортогональности картографической сетки (угол i между меридианами и параллелями), масштабы по главным направлениям (экстремальные масштабы) – наибольший ( ) и наименьший (b) и наибольшее искажение углов (), а также характер искажений (свойства изображения). Эти величины получают с помощью коэффициентов Гаусса через частные производные, взятые по аргументам  и :

; ;

; . (2)

Масштабы по меридианам, параллелям и площадям определяют по формулам

; (3)

; (4)

. (5)

Для контроля используется формула

. (6)

Условием ортогональности картографической сетки является равенство нулю коэффициента f, которое подтверждается вычислением угла i между меридианами и параллелями по одной из формул:

или . (7)

При или угол i равен 90⁰, сетка ортогональна.

Масштабы по главным направлениям (экстремальные) находятся по формулам:

; , (8)

где ,

.

Наибольшее искажение углов определяется по формулам:

, , . (9)

Используют ту из формул, которая упрощает вычисления.

По характеру искажений (свойствам изображения) картографические проекции подразделяют на равноугольные, равновеликие, равнопромежуточные и произвольные. Условия, определяющие свойства изображения:

• условия равноугольности: , , ;

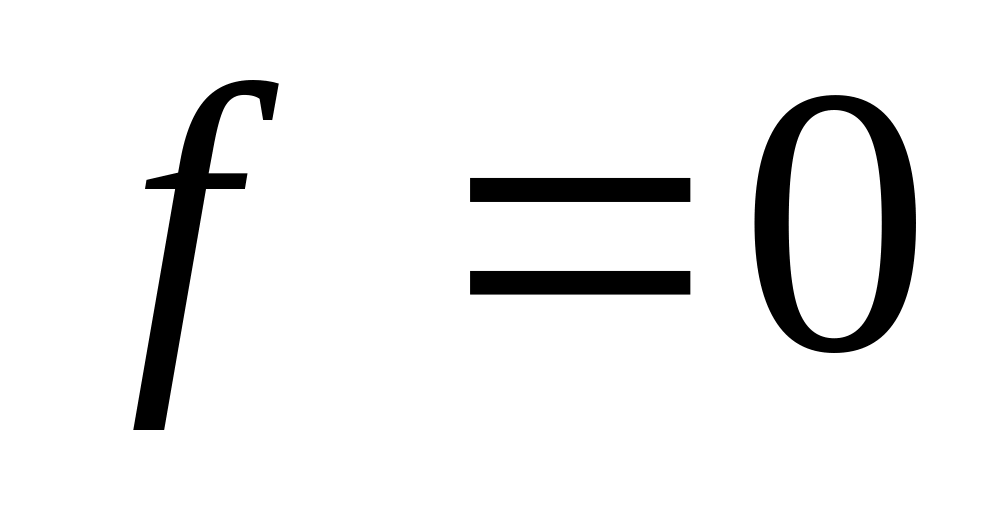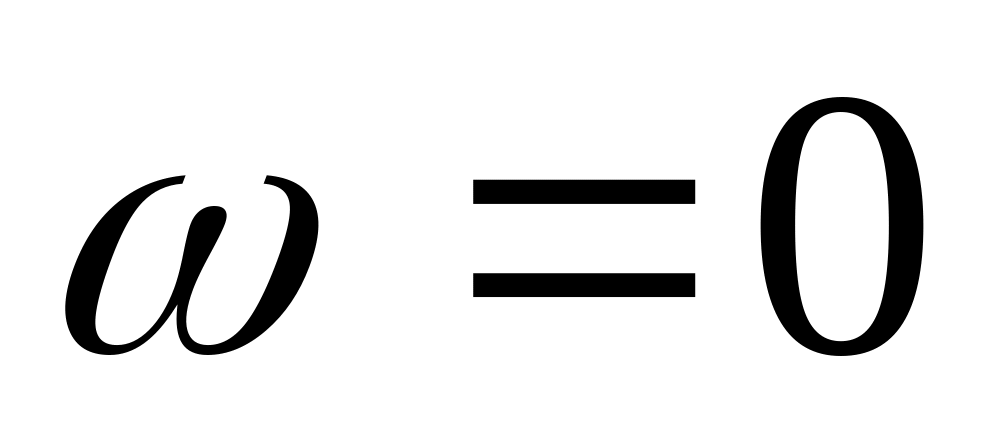• условия равновеликост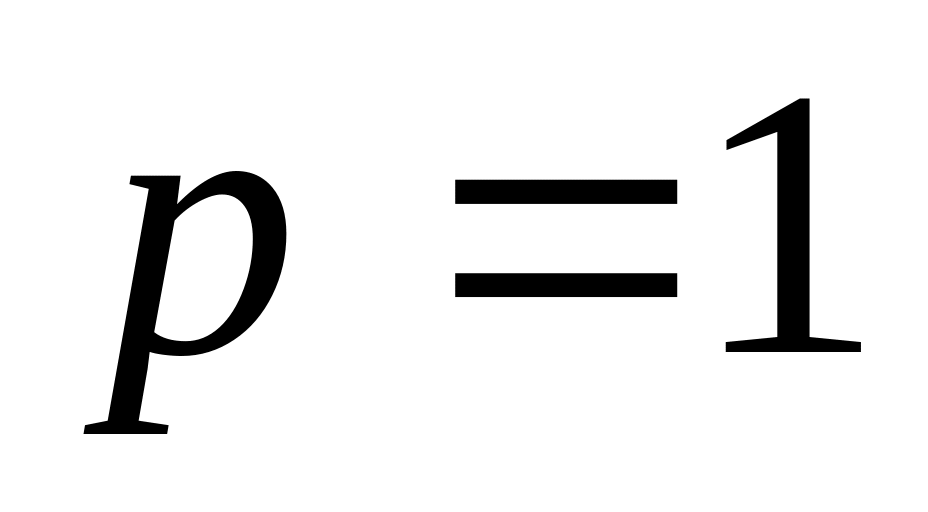и: или ;

• условия равнопромежуточности: или .

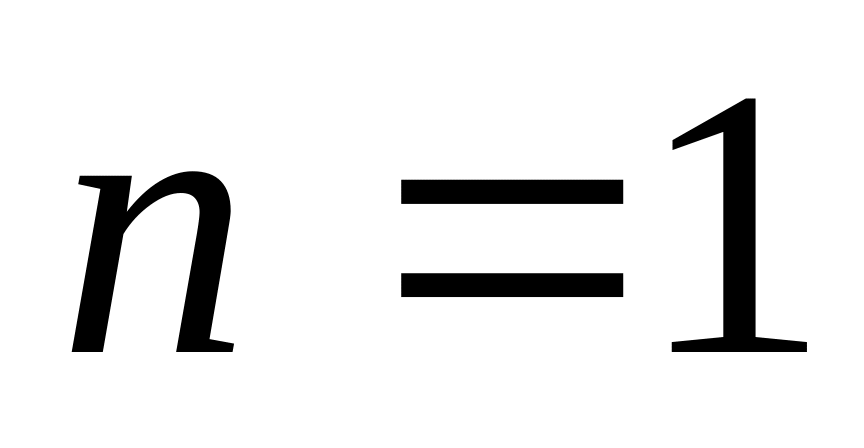Если эти условия не выполняются, то проекция относится к группе произвольных.

Анализ картографических проекций производится для оценки их достоинства.

На картах картографическую проекцию отождествляет картографическая сетка, которая составляет математическую основу создаваемых карт. Картографическая сетка строится через заданный интервал между меридианами и параллелями, называемый частотой сетки. Для ее построения вычисляют прямоугольные координаты узловых точек проекции – точек пересечения меридианов и параллелей через заданный интервал – в заданном главном масштабе.

ЗАДАНИЕ

Анализ картографических проекций

По заданным уравнениям картографической проекции определить:

а) вид сетки меридианов и параллелей, и построить ее;

б) ортогональность картографической сетки;

в) частные масштабы длин и площадей, масштабы по главным направлениям и наибольшее искажение углов;

г) группу проекций по характеру искажений.

Порядок выполнения задания рассмотрим на примере решения уравнений проекции:

.

а) Определение вида сетки меридианов и параллелей.

В данных уравнениях абсциссы и ординаты являются функциями и широты и долготы, следовательно, для получения уравнения меридианов нужно решить совместно исходные уравнения так, чтобы исключить , а для получения уравнения параллелей – исключить из них .

В результате будем иметь уравнение меридианов вида

,

и уравнение параллелей

.

Уравнение меридианов получим делением второго уравнения на первое

.

Это уравнение прямых линий, проходящих через начало прямоугольных координат – географический полюс и пересекающихся под углами, равными разности долгот .

Для исключения из уравнений  возведем в квадрат оба уравнения и почленно сложим полученные уравнения. Уравнение параллелей будет иметь вид

.

Это уравнение концентрических окружностей с центром в точке схода меридианов – географическом полюсе. Из уравнений видно, что при удалении от полюса к экватору, т.е. при уменьшении широты от 90 до 0 радиусы параллелей увеличиваются пропорционально , а расстояния между параллелями уменьшается пропорционально , где и широты соседних параллелей. Максимальным радиусом в проекции будет радиус экватора , следовательно, наибольшей территорией, которую можно изобразить в данной проекции, будет полушарие.

б) Определение ортогональности картографической сетки.

Предварительно возьмем частные производные от уравнений проекций

; ;

; .

Найдем коэффициенты Гаусса:

,

,

,

, значит, картографическая сетка ортогональна.

Для контроля найдем угол между меридианами и параллелями по формуле . , ортогональность сетки подтверждается.

Картографическая сетка в заданной проекции имеет вид

180⁰

135⁰

135⁰

90⁰

90⁰

75⁰

180⁰

60⁰

45⁰

45⁰

45⁰

30⁰

0⁰

Рис. 1

в) Определение частных масштабов длин и площадей, масштабов по главным направлениям и наибольшего искажения углов.

Масштаб по меридианам

изменяется от 0 на экваторе до 1 на полюсе.

Масштаб по параллелям

,

т.е. постоянен, длины параллелей не искажаются.

Масштаб площади

.

Контроль: .

Масштаб площади аналогичен масштабу по меридианам, т.е. изменяется от 0 на экваторе до 1 на полюсе.

Масштабы по главным направлениям (экстремальные масштабы)

;

;

; ; ; .

Так как сетка ортогональна, то главные направления совпадают с меридианами и параллелями. Учитывая, что меньше единицы, в нашем случае лучше принять

, а .

Наибольшее искажение углов найдем по формуле

.

Наибольшего искажения достигают углы на экваторе при и уменьшаются до 0 на полюсе.

г) Определение группы проекций по характеру искажений.

1. Условие равноугольности не выполняется, т.к. хотя , но 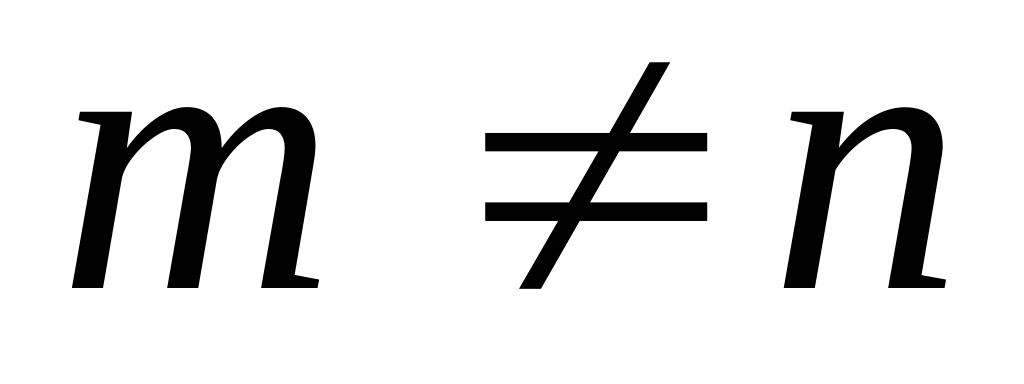и 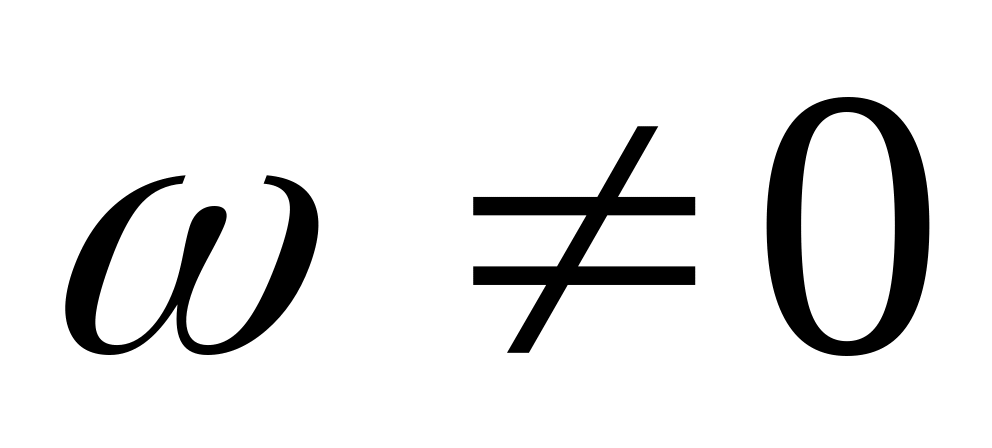, т.е. проекция не равноугольна.

2. Условие равновеликости не выполняется, т.к. и проекция не равновеликая.

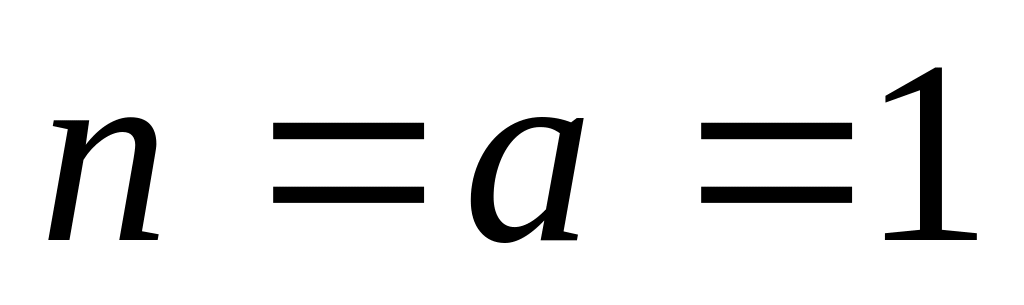3. Так как , то проекция равнопромежуточная по параллелям.

Таблица 1

Варианты индивидуальных заданий

№ варианта	Уравнения проекций	№ варианта	Уравнения проекции
1		14
2		15
3		16
4		17
5		18
6		19
7		20
8		21
9		22
10		23
11		24
12		25
13		26

ЧАСТЬ ВТОРАЯ