
- •Предмет курса «Процессы и аппараты пищевых производств»
- •Классификация процессов и аппаратов пищевых производств
- •Классификационные признаки. Требования к ПиАпп
- •Феноменологический метод
- •Экспериментальный метод
- •Аналитический метод
- •Теория подобия
- •Системный подход
- •Основные физические свойства пищевых продуктов и сырья
- •Плотность
- •Вязкость
- •Теплоемкость
- •Теплопроводность
- •Тепрературопроводность
- •Поверхностное натяжение
- •Механические процессы
- •Резание
- •Шлифование
- •Обработка материалов под давлением
- •Сепарирование сыпучего с/х сырья
- •Пневмосепарирование сыпучего с/х сырья
- •Магнитное сепарирование сыпучего с/х сырья
- •Гидромеханические процессы получения гетерогенных и гомогенных систем
- •Понятие гетерогенных и гомогенных систем
- •Теоретические основы перемешивания
- •Перемешивание жидких сред: пневматическое, циркуляционное, статическое, механическое.
- •Гидромеханические процессы разделения гетерогенных и гомогенных систем
- •Осаждение (отстаивание)
- •Фильтрование
- •Осаждение и фильтрование в поле центробежных сил. Электроосаждение
Классификационные признаки. Требования к ПиАпп
Оборудование пищевых производств насчитывает более двух тысяч единиц, относящихся к самым разным процессам. Изучение столь большой номенклатуры машин и аппаратов невозможно без систематизации знаний, основанной на научно обоснованной классификации.
Основные используемые в настоящее время классификационные признаки оборудования пищевых производств следующие:
- технологическая схема процесса. В соответствии с этим признаком различают аппараты поточные, противоточные и с поперечным током;
- непрерывность процесса. По этому признаку различают аппараты, работающие периодически или непрерывно;
- давление в рабочем объеме. Аппараты могут быть с атмосферным, повышенным или пониженным давлением в рабочем объеме;
- температура процесса. Этот классификационный признак подразумевает разделение аппаратов на работающие при температурах, близких к температуре окружающей среды; при высоких температурах; при низких температурах;
- конструктивные признаки. К ним относится использование конкретных конструктивных элементов (туннели, башни, сферы и т. д.); применение известных конструктивных решений по транспортированию и перемешиванию продуктов (вращающиеся барабаны, ленточные конвейеры, вибропривод, пневмотранспорт и т. д.); способ подвода теплоты (кондуктивный, конвективный, радиационный); способ создания давления (насосом, с помощью столба жидкости и пр.).
Требования к оборудованию. Машины и аппараты пищевых производств должны удовлетворять технологическим, эксплуатационным, конструктивным, эргономическим, экономическим и другим требованиям.
Технологические требования определяются назначением аппарата и принятой технологией ведения процессов в нем. Они конкретизируются в зависимости от типа процесса, агрегатного состояния обрабатываемого продукта, его химического состава и физических свойств. Технологическими требованиями определяются форма рабочего объема аппарата и основные размеры элементов рабочей зоны, температура и давление в ней, скорость движения продуктов и степень турбулизации жидкостных потоков, необходимые площади контакта фаз, дополнительные воздействия на продукт, предотвращение инфицирования и загрязнения продукта.
Эксплуатационные требования чрезвычайно разнообразны. К ним относятся: высокая интенсивность процесса (производительность, отнесенная к какой-либо характеристике аппарата — объему рабочей камеры, площади нагревательных поверхностей); коррозионная устойчивость материалов; расход энергии; надежность; доступность для осмотра и ремонта и др.
Конструктивные требования зависят от многих факторов. К ним относятся: высокая степень унификации и взаимозаменяемости с другим оборудованием данного и родственных предприятий; малая трудоемкость сборки, монтажа и ремонта; удобство транспортировки и ремонта; минимальная масса, в том числе металлоемкость; технологичность изготовления и ремонта.
Эргономические требования включают эстетические требования и требования безопасности, в том числе требования обеспечения нормативных условий труда. Они направлены на предотвращение травм при эксплуатации оборудования, создание здоровых условий труда при безусловном выполнении санитарно-гигиенических требований к оборудованию, создание благоприятных психофизиологических условий для функционирования системы человек- машина - окружающая среда. Все эргономические требования стандартизованы.
Экономические требования формулируются из условия минимизации целевой функции затрат. В свою очередь, целевая функция затрат может учитывать условия проектирования, изготовления, монтажа и эксплуатации.
Основные законы науки о ПиАПП
Расчет машин и аппаратов предусматривает определение массовых потоков перерабатываемых материалов, а также количеств необходимой энергии, оптимальной площади тепломассообменной поверхности (объема) аппарата или продолжительности процесса, основных размеров машин и аппаратов.
Анализ процессов и расчет машин и аппаратов проводят в следующем порядке: составляют материальный и энергетический балансы процесса; исходя из статики, определяют направление течения процесса и условия равновесия; вычисляют движущую силу; на основании кинетики определяют скорость процесса. По данным о скорости процесса и величине движущей силы при найденном оптимальном режиме процесса определяют основной размер аппарата - рабочий объем или рабочую площадь поверхности. По основному размеру определяют все остальные размеры аппарата.
Энергетический баланс (Закон сохранения энергии)
Энергетический баланс. Этот баланс составляют на основе закона сохранения и превращения энергии.
Закон формулируется следующим образом: в изолированной системе сумма всех видов энергии является величиной постоянной, или энергия никогда не создается и не уничтожается — она только переходит из одной формы в другую.
Отсюда следует вывод, что нельзя получить нечто из ничего. Это великое «бухгалтерское» правило оказалось очень полезным. Если обнаруживается изменение энергии, которое не входит в современный список форм энергии, если выясняется, что энергия исчезает или появляется как бы из ничего, то приходится придумывать новый вид энергии, который учел бы эту разницу. Нейтрон, например, был обнаружен вследствие недостачи в энергетическом балансе атомного реактора. Его открыл в 1932 г. английский ученый Джеймс Чэдвик.
Разновидность энергетического баланса — тепловой баланс: количество энергии ΣQвх введенной в процесс, должно быть равно количеству выделившейся энергии:
ΣQвх = ΣQвых+ΣQпотери,
где: ΣQвых - количество отводимой теплоты; ΣQпотери — потери теплоты в окружающее пространство.
Вводимая в процесс теплота ΣQвх складывается из теплоты Q1 поступающей с исходными материалами, подводимой, например, теплоносителями, теплоты Q2 и теплоты физических или химических превращений Q3.
Количество отводимой теплоты ΣQвых складывается из теплоты, уходящей с конечными продуктами и отводимой теплоносителями.
Из теплового баланса определяют расход греющего пара, воды и других теплоносителей.
Материальный баланс (Закон сохранения массы)
Материальный баланс составляют на основании закона сохранения массы (Ломоносов, 1748г): количество поступающих материалов ΣМвх должно быть равно количеству конечных продуктов ΣМвых и возможных потерь ΣМпотери, получаемых в результате проведения процесса:
ΣМвх = ΣМвых+ ΣМпотери
На основании материального баланса определяют выход продукта, т.е. выраженное в процентах отношение полученного количества продукта к максимально возможному. Выход продукта рассчитывают на единицу затраченного сырья.
Материальный баланс составляют для всех веществ либо для одного вещества за выбранную единицу времени или за одну операцию.
Принцип Ле-Шателье
Как же организуется на практике протекание сложных процессов, например процессов массообмена? Основа сложных процессов организации и управления ими — использование объективно существующей природной закономерности самостоятельного перехода любой системы к состоянию равновесия.
Равновесным считают такое состояние системы, которое само устанавливается в ней и не изменяется во времени. Никакие процессы в системе при этом не происходят.
Если каким-либо внешним воздействием вывести систему из состояния равновесия, в ней самопроизвольно начнутся изменения, возвращающие ее в новое состояние равновесия, соответствующее измененным внешним условиям. Это утверждение составляет сущность принципа Ле Шателье. Обусловленные этим принципом явления лежат в основе организации рабочих процессов физико-химической природы.
Чтобы легче понять принцип Ле Шателье, рассмотрим простую химическую реакцию. Два вещества (реактивы) взаимодействуют друг с другом, в результате взаимодействия образуется третье вещество (продукт), которое стремится к расщеплению на исходные вещества. Это можно изобразить в виде следующего уравнения:
A + B <—> C
Двойная стрелка обозначает обратимую реакцию. При протекании прямой реакции слева направо происходит образование вещества C из веществ A и B.
В случае обратной реакции (справа налево) вещество C расщепляется на вещества A и B. Когда эта система находится в химическом равновесии, скорости прямой и обратной реакций одинаковы — в одной точке данной системы образуется молекула вещества C, а где-то в другом месте другая молекула вещества С распадается.
Если в систему добавить избыток вещества A, равновесие временно нарушится, так как вырастет скорость образования вещества C. Но чем быстрее будет расти концентрация вещества C, тем быстрее оно будет расщепляться — пока снова не будет достигнуто равновесие между прямой и обратной реакциями. Тогда скорость образования вещества C из веществ A и B сравняется со скоростью расщепления вещества С на вещества A и B.
Правило фаз Гиббса (Закон термодинамики)
Почему лед и вода, не превращаясь друг в друга, существуют только при 0°С? Чуть изменится температура — и либо лед начнет таять, либо вода начнет замерзать. У воды существует и третье «обличье» — водяной пар. Так вот, могут ли вода, пар и лед существовать в одном сосуде одновременно, не превращаясь друг в друга?
При 0°С в лужах появляются кусочки льда. Первоначально однородная система — жидкая вода — распадается на две части. Их называют двумя разными фазами химического соединения Н2О. То же самое соединение может существовать и в виде третьей фазы — водяного пара.
Жидкость, кристалл и пар — самые привычные примеры разных фаз одного вещества. Однако фазы не обязательно различаются между собой именно агрегатным состоянием.
Хорошо известны две твердые фазы углерода — графит и алмаз. Они имеют разные кристаллические решетки, и это приводит к колоссальному различию их свойств. Фазы могут отличаться друг от друга и по своему химическому составу, и по магнитным характеристикам (магнитная и немагнитная), и по электрической проводимости (нормальная и сверхпроводящая), и по другим свойствам.
Теперь попытаемся ввести понятие фазы более строго. Фазой называется всякая однородная система, т. е. тело, физические свойства которого во всех точках одинаковы. Между разными фазами одной системы обычно существует четко выраженная поверхность раздела.
При изменении внешних условий (температуры, давления, электрического или магнитного полей) фазы могут превращаться друг в друга (это вполне понятно уже на примере воды, пара и льда). Эти процессы так и называются — фазовые превращения.
Подчеркнем одно важное обстоятельство. Линии на диаграмме отделяют друг от друга области устойчивого существования соответствующих фаз. Это отнюдь не означает, будто каждая фаза «живет» только в своей области и не может «залезать» в чужую. Разумеется, может. Мы регулярно наблюдаем это, скажем, весной, когда уже при положительной температуре реки еще полны льдин. Но такое состояние не является устойчивым — лед в реке тает. Этот процесс происходит не мгновенно, а с какой-то конечной скоростью. Если состояние системы перестает меняться во времени, говорят, что в ней установилось равновесие. Диаграмма на рисунке 2 предсказывает только равновесное состояние системы.
Подобные диаграммы называют фазовыми. Ими очень удобно пользоваться: зная температуру и давление, сразу определяем, из каких фаз система будет состоять в равновесии. Определенным значениям давления и температуры на диаграмме соответствует точка. Если она попадает в области устойчивого существования пара, льда или жидкости, то в равновесии система будет состоять из одной соответствующей фазы. Если точка оказывается на линии диаграммы, система в равновесии будет состоять из двух фаз. Из каких именно? Совершенно очевидно: если, например, это — линия раздела «водной» и «ледяной» областей, то из льда и воды. И наконец, при единственном сочетании давления и температуры в равновесии будут находиться все три фазы.
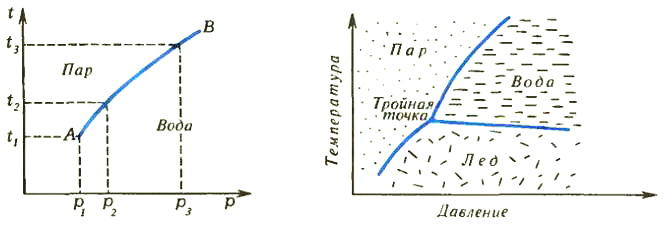
Не почувствовали вы по диаграмме воды, что имеются какие-то законы, регламентирующие «условия жизни» фаз? Посудите сами: в однофазном состоянии система может существовать в широком диапазоне давлений и температур, в двухфазном — только при их определенных комбинациях, а трехфазная область на диаграмме вообще стягивается в точку. Так и хочется представить фазы в роли жильцов коммунальной квартиры: чем больше жильцов, тем меньше свободы у каждого из них.
Теперь пора ввести новое понятие — число степеней свободы. Так в термодинамике принято называть количество внешних параметров, которые в некоторых пределах можно независимо друг от друга менять, не меняя при этом фазового состояния системы. В изучаемом нами случае внешних параметров всего два — давление и температура. А теперь взгляните еще раз на фазовую диаграмму воды (рис. 2). Каждому однофазному состоянию соответствует некоторая площадь, в пределах которой можно свободно варьировать оба параметра. Например, воду как таковую (жидкую) можно нагреть или приложить к ней внешнее давление, или сделать то и другое одновременно (все это, конечно, в некоторых пределах), и при этом фазовое состояние системы в сосуде не изменится — вода так и останется водой. То же самое справедливо в случае льда или пара. Можно сделать вывод, что однофазная система имеет две степени свободы.
В многокомпонентной многофазной системе часть параметров может изменяться независимо, т. е. им можно задавать произвольные значения; оставшаяся их часть является зависимой; их изменения автоматически подстраиваются к изменениям независимых параметров.
Соотношение между числом степеней свободы системы S (числом параметров, которые можно изменять произвольно), числом компонентов К (числом чистых химических веществ системы) и числом фаз F (числом физически однородных по своей массе веществ) определяется правилом фаз Гиббса:
S=K~F+2.
Классификация систем.
По числу компонентов.
1.однокомпонентные,
2.двухкомпонентные,
3.трехкомпонентные.
По числу фаз.
1.однофазные, S = 2
2.двухфазные, S = 1
3.трехфазные, S = 0
По числу степеней свободы.
1. S = 0 – нонвариантные,
2. S = 1 – моновариантные,
3. S = 2 – бивариантные.
В зависимости от числа компонентов и фаз описание состояния системы усложняется с возрастанием компонентности и фазности. Для однокомпонентных однофазных систем состояние можно описать аналитически и графически. Для двухкомпонентных и трехкомпонентных аналитическое выражение затруднено и описание состояния таких систем ведется только с помощью диаграмм.
Фазовые равновесия. Правило фаз Гиббса.
1.Равновесие системы – химическая система находится в равновесии, если ее состояние при заданных условиях внешне во времени не изменяется.
Химическая система.
2.Фаза – иногда фазу определяют как часть системы, отделенной от другой части системы, видимой поверхностью раздела. Более строгое определение фазы – совокупность телесных компонентов, обладающих на всем протяжении одинаковыми физическими, термодинамическими и химическими свойствами.
3. Компонент – или составляющей частью системы называются химически однородные вещества, которые могут быть выделены из системы и существовать вне ее бесконечно долгое время.
Формулировка правила фаз.
Если на какую-то равновесную систему из внешних факторов влияет Т и Р, то число степеней свободы равно числу компонентов прибавить два и вычесть число фаз.
Оно показывает то число переменных, которое можно менять, производя без изменения фаз в системе.
Правило фаз Гиббса определяет соотношение между числом фаз (Ф), компонентов (К), внешних переменных (П) и числом степеней свободы или вариантности (С) термодинамической системы, находящейся в равновесии и записывается следующим образом:
С = К + 2 – Ф;
Цифра 2 в правиле фаз связана с существованием 2-х переменных (температуры и давления), одинаковых для всех фаз. Например, правило фаз Гиббса для постоянного давления запишется как:
С = К +1 – Ф
В этом виде правило фаз применяется для анализа диаграмм фазового равновесия. В случае С = 0 систему принято называть нонвариантной. Она может существовать только при неизменных условиях. Изменение хотя бы одного из параметров системы вызовет изменение числа сосуществующих в системе фаз. При С = 1 система моновариантна. В этом случае только один параметр может быть изменен без одновременного изменения числа фаз; при С = 2 система дивариантна и т. д.
Правило фаз справедливо, если фазы однородны во всем объеме, имеют достаточно большие размеры и отсутствуют полупроницаемые перегородки. Если в системе не происходит химических превращений, то число независимых компонентов равно числу простых веществ, из которых состоит смесь. Если в системе возможны химические взаимодействия, то условия равновесия включают уравнения химических реакций.
Правило фаз Гиббса является основой физико-химического анализа сложных систем, используется для классификации различных случаев химического равновесия.
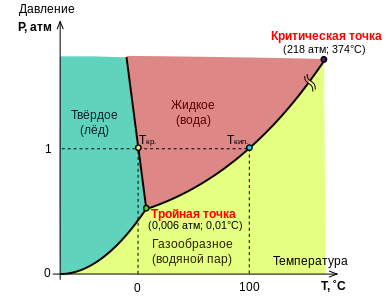
Тройная точка воды — температура 273,16 К и давление 611,657 Па
Методы исследования процессов и аппаратов
