Кеңістіктегі қисыққа жанама

Кеңістікте өзара беттеспейтін екі беттін қиылысу нүктелерінің жиыны кеңістікте қандай да бір болмасын кеңістіктегі қисықты анықтайды ( қарастырылып отырған беттер деңгейлі беттер болмауы тиіс). Айталық , беттер айқындалмаған теңдеулермен берілсін:

=0 (1)

(2)

теңдеулермен берілсін. Егер қисықтың бойынан нүктесінен алсақ (25 сызба ), онда бұл нүкте теңдеуімен анықталатын бетіне де, теңдеуімен анықталатын бетіне де тиісті, олай болса, нүктесінің координаталары (1),(2) теңдеулерді қанағаттандырады:

=0, =0

Алдыңғы тармақтағыдай нүктесінде және беттерінің сәйкесінше нормаль векторлырын құрамыз және беттері днңгейлі беттер болмағандықтын бұл векторлар өзара коллинеар емес деп ұйғарамыз,

25 Сызба

( нүктесінде жүргізілген жазызтықтар өзара беттеспейді). және векторлары коллинеар емес, олай болса,

rang =

векторлары коллинеар емес, олай болса,

векторларын базистік векторлар бойынша жіктелік:

, (3)

Егер екі вектордың көбейтіндісінің екінші қасиетін ескерсек, онда

қисғының жанама түзуінің бағыттаушы вакторы н ормаль векторларының векторлық көбейтіндісі ретінде анықталатынын байқау қиын емес, себебі векторы да, векторы да векторына ортогональ.

Сонымен,

= (4)

векторы қисығының t жанама түзуінің бағыттаушы векторы және векторы келесі формула бойынша есептеледі:

қисығының нүктесінде жүргізілген жанама түзуінің теңдеуі:

(5)

Мұндағы (X,Y,Z)- айнымалылары қисығының ағымдағы нүктесінің координаталары, ал

= , ,

=

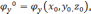
қисық тың берілген нүктедегі жанама түзуіне перпендикуляр және берілген нүкте арқылы өтетін жазықтық қисықтың нормаль жазықтығы деп аталады және нормаль жазықтықтың теңдеуі былай жазылады:

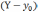(X- )+ + ( )=0 (6)

Нормаль жазықтықтың (6) теңдеуін анықтауыштың қасиетіне сүйене былайша жазуға болады:

=0

Әдебиеттер

1. Атанасян Л.С., Базылев В.Т., Геометрия, ч. II , М., 2001

2. Васильев М.В., Учебное пособие по дифференциальной геометрии , М., 2008

3. Вернер А.Л., Кантор Б.Е. Элементы топологии и дифференциальной геометрии, М ., 2005

4. Выгодский М.Я., Дифференциальная геометрия, М., 2009

5. Гильберт Д., Кон-Фоссен С., Наглядная геотрия, М., 2000

6. Кобаяси Ш., Намидзу К., основы дифференциальной геометрии ч.I, ч.II, М., 2001

7. Исқақов М.Ө., Құлқашаева М.Т., Аналитикалық геометрия мен есептері мен жаттығулары , Алматы, 2002

8. Малаховский В.С., Введение в теории внешних форм. ,Калининград, 2008

9. Закәрин А., юсупов Ж., Геометрия негіздерінің элементтері , Алматы 2008

10. Норден А.П., Краткий курс по дифференциальной геометрии. М., 2008

11. Норден А.П., Пространства аффинной связности , М., 2006

12. Норден А.П., Теория поверхностей , М., 2004

13. Рашевский П.К., Курс дифференциальной геометрии, М, 2000

14. Төлегенов М.О., Дифференциалдық геометриядан методикалық талдау, Алматы, 2001

15. Фиников С.П., Дифференциальная геометрия, М., 2009

Интернет ресурсы:

1. www.google.ru

2. www.google.kz

3. www.kaznpu.kz

4. www.google.com

Ф ҚазҰПУ 0703-12-09 Білім алушыларға арналған пәннің оқу-әдістемелік кешені