Беттің нормалі

Бет

F(x,y,z)=0 (1)

айқындалмаған теңдеумен берілсін.

Егер түзу бетте жататын қандай да бір болмасын қисыққа жанама болса, онда мұндай түзу бетке жанама деп аталады. (22 сызба)

Бетте жататын γ қисығы параметрлік теңдеулермен берілсін:

γ : x=x(t), y=y(t0, z=z(t) (2)

Түзу мен беттің жанасу шартын табамыз, ол үшін γ қисығының нүктелерінің координаталарын беттің теңдеуіне қоямыз, сонда γ қисығы бетке тиісті болғандықтан, төмендегідей тепе-теңдік аламыз:

F (3)

Бұл (3) тепе-теңдік t параметрінің кез келген мәнінде орындалатыны анық. (3) теңдікті t параметрі бойынша дифференциалдаймыз.

· (4)

(4) теңдеудің сол жағы төмендегідей екі шамалардың көбейтіндісінен тұрады:

а) беттің (1) теңдеуінен алынған дербес туындылар:

және

ә) қисықтың нүктесінің x(t), y(t), z(t) координаталарынан алынған туындылар:

; ;

а) және ә) пункттегі туындылар қарастырылатын нүктенің бетте орналасуына ғана тәуелді де, осы қарастырылатын нүктеден өтетін қисықтардан тәуелсіз.Егер

+ (5)

Векторын енгізсек, сонда (4) тепе-теңдік 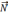және векторларының скаляр көбейтіндісі бойынша былайша жазуға болады.

=0 (6)

Егер беттің нүктесі үшін векторы нольдік вектор, демек, =0 болса, онда беттің мұндай нүктелері беттің ерекше нүктелері деп аталады.

(6) теңдік қисыққа жанама векторы мен қарастырылатын нүктеге тәуелді векторнының өзара ортогональ екенін көрсетеді, ал беттің берілген нүктесі арқылы осы бетте жататын және берілген нүкте арқылы өтетін шексіз көп қисық жүргізуге болады және бұл қисықтар үшін де (6) теңдік орындалады, олай болса, осы қисықтардың жанама түзулерінің түзулерінің бағыттаушы векторлары тек бір ғана векторына ортогональ. Мынадай қорытындыға келдік: беттің берілген жай нүктесінде бетке жанасатын барлық түзулер тек бір ғана жазықтыққа тиісті. (23 сызба)

Беттің берілген нүктесіндегі жанама жазықтық деп осы нүктеде бетке жанасатын түзулердің геометриялық орнын айтамыз (24 сызба)

Жанасу нүктесінен өтіп, жанама жазықтыққа перпендикуляр болатын түзу беттің нормаль түзуі ( қысқаша: беттің нормалі ) деп, ал нормаль түзудің бағыттаушы векторы беттің нормаль векторы деп аталады.

Жанама жазықтықтықтың теңдеуін алу үшін, жанама жазықтықтың беттің берілген нүктесі арқылы өтетін және беттің нормаль векторы (5) формула бойынша өрнектелетінін ескереміз. Жанама жазықтықтың ағымды нүктесінің радиус-векторын деп белгілесек, векторы жанама жазықтықта жатады, олай болса, векторлары ортогональ, демек, бұл векторлардың скаляр көбейтіндісі нольге тең:

( )=0 (7)

(7) теңдеуді = i ⃗+η және радиус-векторларының координаталары арқылы өрнектеп, жанама жазықтықтың теңдеуін аламыз:

(ζ-x)+ (8)

Нормаль түзу мен нормаль вектордың анықтамасынан векторы беттің нормаль векторы болатынын байқау қиын емес (23 сызба). Беттің жай нүктесінде беттің нормаль түзуінің канондық теңдеуі мына түрде жазылады:

(9)

15 - Дәріс.

Тақырып . Кеңістіктегі қисықты екі қиылысуы ретінде анықтау.