
- •Білім алушыларға арналған пәннің
- •Dgt 3305 « Дифференциалдық геометрия және топология »
- •Силлабус
- •1. Пән туралы ақпарат.
- •2.Пәнге қысқаша шолу.
- •5.Күнтізбелік – тақырыптық жоспар.
- •6. Әдебиеттер
- •Бағалаудың критериі
- •8.Оқытушының саясаты.
- •Дәрістердің тезисі
- •(Негізгі ілеспелі үшжағы)
- •Бет және оны параметрлеу
- •Беттің нормалі
- •Кеңістіктегі қисыққа жанама
- •25 Сызба
- •Әдебиеттер
Бағалаудың критериі
-
Жұмыс түрі
АБ -1
АБ - 2
Тест
Қосындысы (ұпай саны)
Лекцияға қатысуы
5
5
10
Семинарға қатысуы
5
5
10
Бақылау жұмысы
5
5
10
СӨЖ тапсырмалары
15
15
30
коллоквиум
40
40
Барлығы I АБ:
30
30
40
100
Лекцияға қатысуы
5
5
10
Семинарға қатысуы
5
5
10
Бақылау жұмысы
5
5
10
СӨЖ тапсырмалары
15
15
30
коллоквиум
30
30
40
100
Барлығы II АБ:
30
30
40
100
Қорытынды бақылау
100
Барлығы
300
8.Оқытушының саясаты.
СӨЖ тапсырмаларын лектор береді. Аралық бақылау практикалық сабақ жүргізетін оқытушымен бірігіп лектор қабылдайды. Студенттің сабаққа қатысуы міндетті. Сабаққа кешігу немесе сабақтан кету сабаққа қатыспаған болып есептеледі.
Сабақта ұялы телефонды пайдалануға және музыка тыңдап басқа істермен айналысуға болмайды. Сабақ үстінде сағыз шайнап, сусын ішуге рұқсат етілмейді.
Дәрістердің тезисі
1- дәріс.
Тақырып. Скаляр аргументті вектор – функция.Айнымалы вектордың шегі.
Скаляр аргументті вектор – функция
Скаляр
аргументті вектор – фукция ұғымын
енгіземіз. V3
кеңістігі евлидтік векторлық кеңістік
, ал
 түзудегі қандай да бір интервал болсын.
Егер
интервалының
қандай да бір болмасын t санына векторлық
V3
кеңістігінің
белгілі бір векторы сәйкес болса, онда
бұл векторды
түзудегі қандай да бір интервал болсын.
Егер
интервалының
қандай да бір болмасын t санына векторлық
V3
кеңістігінің
белгілі бір векторы сәйкес болса, онда
бұл векторды
 арқылы белгілеп ,
интервалындағы скаляр t аргументінің
вектор-функциясы деп атаймыз.
арқылы белгілеп ,
интервалындағы скаляр t аргументінің
вектор-функциясы деп атаймыз.
Скаляр
айнымалыға тәуелді вектор-функцияны
физикадан, механикадан көптеп кездестіруге
болады. Мәселен, егер
 =
= векторы қозғалыстағы M нүктесінің
радиусы- векторы болса, онда бұл
векторы уақытқа, яғни скаляр шамаға
байланысты өзгеріп отырады.
векторы қозғалыстағы M нүктесінің
радиусы- векторы болса, онда бұл
векторы уақытқа, яғни скаляр шамаға
байланысты өзгеріп отырады.
t параметріне скаляр аргументті тәуелді вектор-функцияны былайша жазып көрсетеміз:
=

Егер
B= векторлық V3
кеңістігінің базисі болса, онда
векторлық V3
кеңістігінің базисі болса, онда
 вектор-функциясын анықтау үшін, бұл
вектор-функцияның координаталарын осы
t аргументінің функциясы ретінде
анықтауымыз керек, олай болса,
векторы
B базисі бойынша былай жіктеледі:
вектор-функциясын анықтау үшін, бұл
вектор-функцияның координаталарын осы
t аргументінің функциясы ретінде
анықтауымыз керек, олай болса,
векторы
B базисі бойынша былай жіктеледі:
=
=
x + y
+ y +
+
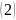
Бұл (2) теңдікпен берілген вектор-функциясы скаляр t аргументіне тәуелді келесі үш теңдеудің берілуімен пара- пар:
x=x(t), y(t), z=z(t). (3)
Айнымалы вектордың шегі
Шексіз аз векторлар ұғымын енгіземіз.
Егер
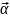 вектор-функциясының ұзындығы нөлге,
ұмтылса , онда мұндай вектор-функцияны
шексіз аз вектор деп айтамыз да, мынадай
белгілеуді пайдаланамыз:
=
вектор-функциясының ұзындығы нөлге,
ұмтылса , онда мұндай вектор-функцияны
шексіз аз вектор деп айтамыз да, мынадай
белгілеуді пайдаланамыз:
=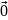 (
( →0)
→0)
Вектор-функцияның шегі ұғымы математикалық анализ курсіндегі шектің анықтамасы тәрізді енгізіледі.
Егер t
аргументі t0
шамасына ұмтылғанда,
 0
вектор-функциясы
шексіз аз вектор болса, демек,
0
вектор-функциясы
шексіз аз вектор болса, демек,
│ 0│= 0 , t→t0
орындалса,
онда скаляр t аргументі t0
аргументіне ұмтылғанда тұрақты
 0
векторы
0
векторы
 вектор-функциясының
шегі деп атап, былайша жазамыз:
вектор-функциясының
шегі деп атап, былайша жазамыз:
 (t)
=
0
,
(t)
=
0
,
немесе
→ 0 , t→t0
немесе
- 0= , →
Вектор-функциясының үздіксіздігі де скаляр анализдегідей анықталады.
Егер t
аргументі t0
аргументіне ұмтылғанда,
векторы
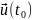 шегіне ұмтылса, онда
вектор-функциясы аргументтің t=t0
мәнінде үздіксіз деп аталады. Үздіксіздіктің
бұл анықтамасын шектің анықтамасымен
былай жазуға болады:
шегіне ұмтылса, онда
вектор-функциясы аргументтің t=t0
мәнінде үздіксіз деп аталады. Үздіксіздіктің
бұл анықтамасын шектің анықтамасымен
былай жазуға болады:
t→t0
,
│ │→0
│→0
Егер интервалының әрбір нүктесінде функциясы үздіксіз болса, онда вектор-функциясы интервалында үздіксіз деп аталады.
Вектор-функцияның қосындысы мен көбейтінділерінің шегінің келесі қасиеттерін атап өтеміз:
1.
lim (
±
 ) = lim
±
) = lim
±
2. lim ( · ) = lim ·
Оқырмандарға бұл қасиеттерді өз бетінше дәлелдеуді ұсынамыз.
 вектор-функциясының
туындысы Лейбництің белгілеуі бойынша
(штрих), не болмаса Ньютонның белгілеуі
бойынша(функцияның үстінен нүкте
қойылады) белгілейміз:
вектор-функциясының
туындысы Лейбництің белгілеуі бойынша
(штрих), не болмаса Ньютонның белгілеуі
бойынша(функцияның үстінен нүкте
қойылады) белгілейміз:
̀̀̀′
=
 ,
,
 =
=
 .
.
2 - Дәріс.
Тақырып. Ұзындығы тұрақты вектор – функцияның және бағыты тұрақты вектор – функцияның туындысы
 .
Ұзындығы тұрақты вектор-функция. Егер
=
вектор-функциясының бағыты өзгергенде
ұзындығы тұрақты болса, онда
.
Ұзындығы тұрақты вектор-функция. Егер
=
вектор-функциясының бағыты өзгергенде
ұзындығы тұрақты болса, онда
 болатыны түсінікті. Бұдан
болатыны түсінікті. Бұдан

Соңғы теңдіктің оң және сол жақтарын t аргументі бойынша дифференцияалдаймыз:

вектор-функциясы
нөлдік вектордан өзгеше болғандықтын
және екі вектордың скаляр көбейтіндісінің
анықтамасы бойынша
 -функциясы
-функциясы
 (t)=
вектор-функциясына
ортогональ болатынын байқаймыз:
(t)=
вектор-функциясына
ортогональ болатынын байқаймыз:

Сонымен біз мына лемманы дәлелдедік:
Лемма-1. Ұзындығы тұрақты вектор-функциядан алынған туынды вектор-функция берілген вектор-функцияға ортогональ.
 Бағыты
тұрақты вектор-функция. Лемма-2.
вектор-функциясының бағыты тұрақты
болуы үшін
вектор-функциясы мен
Бағыты
тұрақты вектор-функция. Лемма-2.
вектор-функциясының бағыты тұрақты
болуы үшін
вектор-функциясы мен
 туынды вектор-функциясының коллинеар
болуы қажетті және жеткілікті. Айталық
вектор-функциясының ұзындығы
өзгеріп,бірақ бағыты тұрақты болсын.
туынды вектор-функциясының коллинеар
болуы қажетті және жеткілікті. Айталық
вектор-функциясының ұзындығы
өзгеріп,бірақ бағыты тұрақты болсын.
Бұл жағдайда, мұндай векторларды былайша жазуға болады:
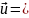 u
u (1)
(1)
мұнда ,
ал
,
ал
 векторы
вектор – функциясының бірлік векторы
:
векторы
вектор – функциясының бірлік векторы
:
 (1) теңдікті t параметрі бойынша
дифференциалдаймыз:
(1) теңдікті t параметрі бойынша
дифференциалдаймыз:
=
 ′
(2)
′
(2)
(1) теңдіктен
=
 (3)
(3)
(2) және (3) теңіктерден:
̀̀̀
′=
Егер
 деп
белгілесек, онда соңғы теңдіктен:
деп
белгілесек, онда соңғы теңдіктен:
̀̀̀
′=
 (4)
(4)
Бұл теңдік , ̀̀̀′ вектор – функцияларының коллинеар болатынын көрсетеді.
, ̀̀̀′(t) вектор – функциялары коллинеар болсын, онда ̀̀̀′ = теңдігі орындалады. (1) теңдікті векторының бағыты тұрақты емес деп ұйғарып дифференциалдаймыз:
̀̀̀
′= u′
+ u

̀̀̀ ′ векторының мәнін (4) формула бойынша қоямыз:
 u
u + u
+ u
бұдан векторының мәнін (1) формула бойынша қойып алатынымыз:
 = u
+ u
′
= u
+ u
′
Бұл
теңдеудің оң және сол жақтарын
 векторына скаляр көбейтеміз:
векторына скаляр көбейтеміз:
 u′
u′
 ′
+ u
′
+ u

Алдыңғы
kемма бойынша
 және
векторлары
ортогональ, олай болса,
және
векторлары
ортогональ, олай болса,
 =0
сондықтан, соңғы теңдіктен табатынымыз:
=0
сондықтан, соңғы теңдіктен табатынымыз:
u =0
=0
немесе

Олай болса, векторы тұрақты демек, вектор-функциясының бағыты тұрақты.
Лемма дәлелденді
3 - Дәріс.
Тақырып. Жазық қисық туралы ұғым
Қисық ұғымы – дифференциалдық геометрияда бір мәнді анықтала бермейтін күрделі ұғымдардың бірі. Қисықты біз интуитивті түрде шексіз аз аймақта түзуге ұқсас деп түсіндіреміз.
Мәселен, γ қисығының шексіз өзара жақын A және B нүктелерінің аралығындағы нүктелер жиыны түзудің бөлігіне ұқсас ( 4- сызба).
Жазықтықта тік бұрышты Oxy координаталар системасы берілсін. Аналитикалық геометрия курсынан:
F (1)
(1)
теңдеуін қанағаттандыратын жазықтықтың нүктелерінің жиыны белгілі бір фигураны – жазықтықта қандай да бір болмасын қисықты анықтайтыны белгілі.
Дифференциалдық геометрияның әдісі дифференциалдауға тәуелді болғандықтан, қарастырылатын функциялар бір мәнді және қанша рет болса, сонша рет дифференциалданады (туынды табылады) деп ұйғарамыз.
Қисық сызықтың (қисықтың) анықтамасын береміз.
Элементтері нүктелер болатын E және F жиындарын қарастырамыз. Егер E жиынынынң шексіз жақындайтын нүктелеріне F жиынының шексіз жақындайтын нүктелері сәйкес келетіндей биекция (өзара бірмәнді сәйкестік) берілсе, онда мұндай сәйкестік топологиялық, не үздіксіз сәйкестік деп , ал бұл екі жиынды топологиялы эквивалентті деп атайды.
Анықтама
бойынша, егер ρ(x,y) болса, онда ρ(f(x),f(y))
болса, онда ρ(f(x),f(y)) , мұнда
, мұнда
 шексіз аз шамалыр. Бұл анықтаманы қисыққа
байланысты айталық.
шексіз аз шамалыр. Бұл анықтаманы қисыққа
байланысты айталық.
Егер түзудің бөлігіне (кесіндісіне) қандай да бір жиын топологиялы эквивалентті болса, онда ол қарапайым доға деп аталады.
Мәселен, 6-сызбада жиыны қарапайым доға. Өзара бірімен бірі жалғасатын шектеулі және санаулы қарапайым доғалардан тұратын жиынды қисық деп айтады. Әдетте , геометриялық обьектілер – қисықтар мен беттер шексіз аз аймақта қарастырылады, бұл дифференциалдық геометрияның әдісі және мұндай микроскопиялық зерттеу қисық пен беттің кейбір ортақ заңдылықтарын байқауға мүмкіндік береді.
AB доғасы
түзуідің
 кесіндісіне топологиялы бейнеленеді
және доғаның бір М нүктесіне кесіндінің
бір
кесіндісіне топологиялы бейнеленеді
және доғаның бір М нүктесіне кесіндінің
бір
 нүктесі сәйкестендірілді деп ұйғарайық.
Түзудегі
нүктесі тек абсциссасымен анықталады.
нүктесі сәйкестендірілді деп ұйғарайық.
Түзудегі
нүктесі тек абсциссасымен анықталады.
Егер АВ доғасының нүктелерін кесіндінің нүктелеріне бейнелейтін заң белгілі болса, онда кесіндідегі нүктесінің t абсциссасы нүктесінің орнын анықтап қана қоймай , қисықтағы М нүктесінің де орналасуын анықтайды (7- сызба) . Доғаның нүктелері мен сан өсіндегі кесіндісінің сандарының арасындағы сәйкестік бір мәнді және үздіксіз. Егер осындай, доғаның нүктелері мен түзудегі (кесіндідегі) сандардың арасында сәйкестік жүзеге асырылса, онда доға параметрленді деп аталады, ал t параметрі өзіне сәйкес М нүктесінің параметрі деп аталады. Кез келген доғаны берілген кесіндіге шексіз көп әдістермен топоплогиялы бейнелеуге болады, сонда әрбір әдіске сай белгілі бір параметрленуі сәйкес болады.
4 - Дәріс.
Тақырып. Қисыққа жанама түзу
γ қандай да бір қисық болып, ал А нүктесі γ қисығына тиісті нүкте болсын. γ қисығынан А нүктесінен өзге В нүктесін алып АВ қиюшы түзуін жүргіземіз.
В нүктесі қисықтың бойымен жылжып, А нүктесіне ұмтылғанда АВ қиюшы түзуінің шектік lA жағдайы γ сызығына А нүктесінде жүргізілетін жанама деп аталады.
Егер lA түзуі А нүктесінде жүргізілген жанама болса, онда В нүктесі А нүктесіне ұмтылғанда АВ түзуі мен жанама lA түзуінің арасындағы бұрыштың шамасы нөльге ұмтылады. Осы айтылғандарды математикалық белгілеумен былайша жазамыз:
 lA
lA
немесе
 lAB
lAB
Бұл анықтамадан жанама түзу бар болса, оның тек жалғыз болатынын көреміз (шек жалғыз).
Қисық = параметрлік теңдеуімен берілсін:
γ : = (1)
γ
қисығының А және В нүктелеріне аргументтің
t және t+ мәндері сәйкес келіп, бұл нүктелердің
радиус – векторлары
және
мәндері сәйкес келіп, бұл нүктелердің
радиус – векторлары
және
 болсын, сонда
болсын, сонда

 =
=


= =
=
 векторы қиюшы АВ түзуінің бағыттаушы
векторы. Егер
векторы қиюшы АВ түзуінің бағыттаушы
векторы. Егер
 болса, онда
болса, онда
 және
векторлар бағыттас. Ал
және
векторлар бағыттас. Ал
 болса, онда бұл векторлардың бағыттары
қарсы болады. Егер В нүктесі қисық
бойымен жылжып , А нүктесіне ұмтылса ,
онда
өсімшесі нoльге ұмтылады және
болса, онда бұл векторлардың бағыттары
қарсы болады. Егер В нүктесі қисық
бойымен жылжып , А нүктесіне ұмтылса ,
онда
өсімшесі нoльге ұмтылады және
 =
=
 (2)
(2)
соңғы
(2) теңдік математикалық анализ курсынан
белгілі. Олай болса,
'
 векторы
lA
жанама
түзуінің бағыттаушы векторы.
векторы
lA
жанама
түзуінің бағыттаушы векторы.
Біз бұдан мынадай қорытындыға келеміз: параметрлік теңдеумен берілген қисықтың нүктесінің радиус- векторынaн t параметрі бойынша алынған туынды ' векторы жанама lA түзуінің бағыттаушы векторы болады.
Жанама lAB түзуінің теңдеуін қорытып шығару үшін кеңістікте тік бұрышты Oxyz декарт коодинаталар системасын енгіземіз. векторын базистік векторлыр бойынша жіктеп жазайық:
 (3)
(3)
Сонда lA жанама түзуінің бағыттаушы ' векторы былайша жазылады:
′ x'
+y'
x'
+y' z'
z'
 нүктесінен
өтетін , бағыттаушы векторы
'
нүктесінен
өтетін , бағыттаушы векторы
'
 x'
x'
 y'
z'
y'
z' болатын жанама lА
түзуінің конондық теңдеуі мына түрде
жазылады:
болатын жанама lА
түзуінің конондық теңдеуі мына түрде
жазылады:
lА:
 ( 4)
( 4)
 )
)
С нүктесі
жанама lА
түзуінің ағымды нүктесі және бұл С
нүктесінің радиус – векторы
 болсын.
болсын.
 және
'
векторлары коллинеар болғандықтан, R
нақты сандар жиынында жататын λ саны
табылып, мына теңдік орындалады ( екі
вектордың коллинеарлық шарты) :
және
'
векторлары коллинеар болғандықтан, R
нақты сандар жиынында жататын λ саны
табылып, мына теңдік орындалады ( екі
вектордың коллинеарлық шарты) :

ал
 (5)
(5)
 радиус-
векторларын және (5) теңдікті ескеріп,
алдыңғы теңдіктен алатынымыз:
радиус-
векторларын және (5) теңдікті ескеріп,
алдыңғы теңдіктен алатынымыз:
 =
=
 '
(6)
'
(6)
(6) теңдеу қисықтың жанама түзуінің векторлық (параметрлік) теңдеуі деп аталады.
Жазықтықтағы қисық үшін (4) теңдеу былайша жазылады:
 ,
)
(7)
,
)
(7)
Егер қисық y=y(x) айқын теңдеуімен берілсе, онда t параметрі ретінде x- ті қабылдаймыз, сонда:
x′=1 , y′= y′
(7) теңдеу мына түрге келтіріледі:
Y-
y(t) = y′ (8)
(8)
Егер
қисықтың t=t0
параметріне сай
(t0)
=
0
векторының туынды
 векторы
нольдік вектор болса, онда жанаманың
теңдеуін жоғарыда айтылған әдіспен
анықтауға болмайды.
векторы
нольдік вектор болса, онда жанаманың
теңдеуін жоғарыда айтылған әдіспен
анықтауға болмайды.
Алдағы кезде қажет болатын бірнеше анықтамаларды берейік.
Анықтaма. Қисықтың нүктесінің ралиус-векторынан алынған ' туынды векторы нөлдік вектор болатын нүктелер қисықтың ерекше нүктелері деп аталады.
Ерекше нүктенің радиус – векторы осы нүктенің маңайында Тейлор формуласына жіктесе , онда мұндай нүкте елеусіз нүкте деп аталады.
Тейлор формуласы вектор – функция үшін былай жазылады:
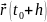 =
(t0)
+
'(t0)
h +
=
(t0)
+
'(t0)
h +
 ٰٰٰٰ
ٰٰ
(t0)
+ …+
ٰٰٰٰ
ٰٰ
(t0)
+ …+
 n-1(t0)
+ Rn
n-1(t0)
+ Rn
мұндағы Rn қалдық мүше:
Rn=
 (n)
(t′)
, t′
€
(n)
(t′)
, t′
€

Егер t=t0 нүктесінде бірінші туындысынан бастап (k-1) -ші ретті туындысына дейінгі туынды векторлар нөлдік вектор деп ұйғарсақ, онда Тейлор формуласы былай жазылады:
=
(t0)+ (
(
 )+α)
)+α)

Және
 векторына сәйкес нүктелерден өтетін
қиюшы түзудің бағыттаушы векторы мына
түрде табылады:
векторына сәйкес нүктелерден өтетін
қиюшы түзудің бағыттаушы векторы мына
түрде табылады:
 =
(
)+
),
=
(
)+
),
соңғы
теңдікте, егер
 ондa
векторы шексіз аз векторға ұмтылатын
вектор.
ондa
векторы шексіз аз векторға ұмтылатын
вектор.
Нүктелер шексіз жақындағанда қиюшы вектордың шектік орналасуы жанама түзудің бағытын анықтайды, сонымен:
 =
)
=
)
векторы елеусіз нүктедегі жанаманың бағыттаушы векторы, олай болса, жанаманың (4) канондық теңдеуі былай жазылады:
 .
(9)
.
(9)
ٰЖанаманың
басқа теңдеулерін алу үшін
 және
векторлары базистік
және
векторлары базистік
 векторлары бойынша жіктеп жазамыз:
векторлары бойынша жіктеп жазамыз:
 (10)
(10)
 (11)
(11)
(1), (10), (11) теңдіктерден:
X=x(t)
+ λ
 ,
,
Y=y
(t) + λ (t) , (12)
(t) , (12)
Z=z(t)+
λ (t).
(t).
(12) теңдеулер қисықтың нүктесіндегі жанаманың параметрлік теңдеулері деп аталады. (12) теңдеуден λ параметрін шығарып , жанаманың (4) түрдегі канондық формуласын аламыз.
Жазық қисық (жазықтықтағы қисық)
γ: x=x(t) , y = y (t) (13)
параметрлік теңдеуімен берілсін. (13) теңдеулерден t параметрін шығарып, қисықтың
F(x,y) = 0 (14)
түріндегі айқындалмаған теңдеуін аламыз. ( z=0 болғандықтан, қисық Oxy жазықтығында жатыр). (13)теңдеудегі x пен y айнымалыларының мәнін (14) теңдеуге қойып, t параметрінің кез- келген мәнінде орындалатын
F(x(t)
, y(t))
 0
0
тепе- теңдігін аламыз.
Бұл теңбе-теңдікті тәуелсіз t параметрі бойынша дифференциалдай-мыз:
 (15)
(15)
Соңғы
теңдеудегі Fx
=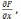 Fy=
Fy=
 дербес туындылардың ең болмағанда
біреуі нөлге тең емес деп ұйғарып,
дербес туындылардың ең болмағанда
біреуі нөлге тең емес деп ұйғарып,
 =y'
шамасын
табамыз, сонда:
=y'
шамасын
табамыз, сонда:
y'= Жанаманың теңдеуін былайша жазамыз:
Жанаманың теңдеуін былайша жазамыз:


 (t)
= (Y-y(t)
(t)
= (Y-y(t) 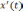 )
(16)
)
(16)
(14)
теңдеуден  =
-
=
-  бұл мәнді соңғы теңдеуге қойып, қисық
айқындалмаған теңдеумен берілгенде
бұл мәнді соңғы теңдеуге қойып, қисық
айқындалмаған теңдеумен берілгенде
 нүктесінде жүргізілген жанаманың
теңдеуін аламыз:
нүктесінде жүргізілген жанаманың
теңдеуін аламыз:
(X-x) Fx + (Y- y) Fy = 0 (17)
Анықтама: Қисықтың берілген M0 нүктесіндегі нормалі деп осы нүктеден өтетін және осы нүктедегі қисықтың жанамасына перпендикуляр болатын түзуді айтады. Ал жазық қисықтың нормалі деп осы жазықтықта жататын және жанасу нүктесінде жанамаға перпендикуляр болатын түзуді айтамыз.
Аналитикалық
геометриядан нормаль түзудің бұрыштық
коэффиценті шамасы бойынша жанаманың
коэффициентіне кері, ал таңбасы бойынша
қарама- қарсы екендігі белгілі: 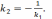 (16) және (17) теңдеулер мына түрге
келтіріледі:
(16) және (17) теңдеулер мына түрге
келтіріледі:
Y-y= (18)
(18)
Y-y= (19)
(19)
Қисықтың жанасу нүктесіндегі нормаль түзулерінің теңдеулері төмендегідей болады:
Y-y=
Y-y=
немесе
 (t)
+ (Y-y(t))
=0,
(t)
+ (Y-y(t))
=0,

Соңғы
теңдікті жазықтықтағы түзудің канондық
теңдеуімен салыстырып, 
 векторы қисықтың нормалінің бағытаушы
векторы болатынын көреміз (10- сызба).
векторы қисықтың нормалінің бағытаушы
векторы болатынын көреміз (10- сызба).
5 - Дәріс.
Тақырып. Қисықтың доғасының ұзындығы
Айталық,
γ
тұйық қисық болмасын, ал А және В нүктелері
γ
қисығының әртүрлі нүктелері болсын.
Ұштары А және В болатын γ
қисығының АВ доғасының ұзыныдығы деп
А мен В нүктелерінің арасындағы нүктелер
жиыны мен А және В нүктелерінен тұратын
жиынды айтамыз және оны  деп белгілейміз. Ал АВ доғасының ұзындығы
былайша анықталады: доғаның ұзындығынын
осы доғаға іштей сызылған сынық
сызықтардың қосындысының шегі ретінде
анықтайды және бұл шекті анықтауда
келесі екі шарттың орындалуы тиіс :
деп белгілейміз. Ал АВ доғасының ұзындығы
былайша анықталады: доғаның ұзындығынын
осы доғаға іштей сызылған сынық
сызықтардың қосындысының шегі ретінде
анықтайды және бұл шекті анықтауда
келесі екі шарттың орындалуы тиіс :
1) сынық сызықтардың саны шексіз өседі,
2) әрбір сынық сызықтың ұзындығы нольге ұмтылады.
Қисық
γ
: ,
t €
,
t €  (1)
(1)
векторлық теңдеумен берілсін.
АВ
доғасын n бөлікке бөліп, бөлу нүктелерін
A= деп белгілейміз. Бұл нүктелерді қосып
(11-сызба)
деп белгілейміз. Бұл нүктелерді қосып
(11-сызба)  штей
сызылған
штей
сызылған сызық аламыз. Бұл сынық сызықтың әрбір
бөлігі өздеріне сәйкес доғалардың
хордасы болады.
сызық аламыз. Бұл сынық сызықтың әрбір
бөлігі өздеріне сәйкес доғалардың
хордасы болады.  кесіндісі
анықтайтын
кесіндісі
анықтайтын 
 =
=  -
- 
Егер
 деп
белгілесек, онда
деп
белгілесек, онда

Іштей
сызылған  сынық қисығының ұзындығы
сынық қисығының ұзындығы  хордаларының қосындысына тең:
хордаларының қосындысына тең:
 =
=
 . (2)
. (2)
 Функция
өсімшесі
Функция
өсімшесі  өсімшесіне сәйкес келсе, онда (2) формуламен
өрнектелетін қосындыны былай жазуға
болады:
өсімшесіне сәйкес келсе, онда (2) формуламен
өрнектелетін қосындыны былай жазуға
болады:
=

 (3)
(3)
t параметінің мәні қандай да бір болмасын аралығына тиісті болса және өсімше нольге ұмтылса, онда өсімшелердің қатынасы мен туындының айырымы нөлге ұмтылады: Келесі айырымды қарастырайық:
 -
-  =
= 
Бұл абсолют шамалардың айырымы шексіз аз болатыны ақиқат, бұл теңдіктен:
 +
+ 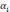
 қосындысын былайша жазамыз:
қосындысын былайша жазамыз:
=
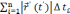 +
+ 
өсімшесі нөлге ұмтылғанда екінші қосылғыштың нольге ұмтылатыны анық. Сонымен :

Ал
теңдіктің оң жағындағы қосынды  функциясының интегралдық қосындысы,
демек ,
функциясының интегралдық қосындысы,
демек ,
S=
 =
= 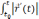 dt (4)
dt (4)
Сонымен доғаның ұзындығы (4) формула бойынша есептеледі. Кеңістікте қисық
x=x(t) , y = y(t) , z=z(t) (5)
параметрлік теңдеулермен берілсін, сонда
 =
=
Олай болса (4) формула былай жазылады:
 (6)
(6)
 Жазықтықтағы қисық үшін z=0 , демек (6)
формуладан жазықтықтағы қисықтың
доғасының ұзындығының формуласын
аламыз:
Жазықтықтағы қисық үшін z=0 , демек (6)
формуладан жазықтықтағы қисықтың
доғасының ұзындығының формуласын
аламыз:
S= dt (7)
dt (7)
Егер
 жазықтығында γ қисығы поляр координаталар
системасында
жазықтығында γ қисығы поляр координаталар
системасында
γ: ρ =ρ(φ)
полярлық теңдеуімен берілсе, онда φ бұрышын параметр ретінде қабылдап, қисықтың парметрлік теңдеуіне көшуге болады (z=0):

Бұл теңдеулерден φ параметрі бойынша туынды табамыз:


x' пен y' айнамалыларының бұл мәндерін (7) формулаға қойып есептейміз, сонда:
 dφ
dφ
Егер жазықтықтағы γ қисығы
γ: y=y(x) (8)
айқын теңдеуімен берілсе, онда x=t параметрін енгізіп, қисықтың (8) теңдеуін былайша жазамыз:
x=t, y=y(t)
Бұдан.
 (7) формулаға қойып, қисық айқындалған
теңдеуімен берілгенде оның доғасының
ұзындығын есептейтін формуланы аламыз:
(7) формулаға қойып, қисық айқындалған
теңдеуімен берілгенде оның доғасының
ұзындығын есептейтін формуланы аламыз:
 dx
dx
Енді қисықтың доғасының ұзындығын есептеуге мысал келтірейік.
1- мысал. x=a cosu, y=a sinu, z=bu Винттік сызығының O(u=0) нүктесінен бастап қисықтың кез келген А нүктесіне дейінгі доғасының ұзындығын табайық.
Алдымен
 туынды екторын тауып,туынды
туынды екторын тауып,туынды  :
:
=
x,y,z айнымалыларынан t параметрі бойынша туынды табамыз:
x’ = -a sinu , y’ = a cosu, z’ = b,
сонда
 .
Олай болса
.
Олай болса
ds= =
= du
du
демек,
ds= du
du
бұдан
S= u
u
6 - Дәріс.
Тақырып. Қисықтың теңдеуінде параметр ретінде доғаның ұзындығын қабылдау.
Қисықтық қасиеттерін зерттеу барысында қисықтың қандай да бір болмасын теңдеуін қарастырамыз, ал қисықтың қарастырылып отырған теңдеуі қайсыбір (афиндік, не тік бұрышты не поляр координаталар және т.б системаға) координаталар системасына тәуелді болатынын байқаймыз.
Қисықты координаталар системасынан тәуелсіз теңдеу арқылы анықтап зерттеуге бола ма, демек, қисықтық теңдеуі қисықтың тек қана геометриялық формасына тәуелді, яғни қисықтың геометриялық формасымен анықтауға бола ма деген сұрақтың тууы орынды.
Біз бұл параграфта қисықтың мұндай теңдеуін құруға болатынын көретеміз.
Қисық
 (t)
параметрлік теңдеуімен берілсін.
Қисықтан t=
(t)
параметрлік теңдеуімен берілсін.
Қисықтан t=
 нүктесін шартты түрде қисықтың бастапқы
нүктесі деп атайық.
нүктесін шартты түрде қисықтың бастапқы
нүктесі деп атайық.
Басы
 ,
ұшы кез келген А нүктесінде болатын
,
ұшы кез келген А нүктесінде болатын
 доғасының ұзындығы мына формула бойынша
есептеледі :
доғасының ұзындығы мына формула бойынша
есептеледі :
 dt=
dt=  (1)
(1)
 =
= ds =
ds = (2)
(2)
Демек, доғаның ұзындығы t параметріне тәуелді , t параметрі өссе онда доғаның ұзындығы өсіп, ал t параметрі кемісе, онда доғаның ұзындығы кемиді және t параметрінің белгілі бір мәніне s доғасының бір ғана мәні сәйкес келеді, басқаша айтқанда (1) формула қисықтың s доғасының ұзындығын t параметрі бойынша дифференциалданатын бір мәнді функция ретінде анықтайды.
(2)
формуладан  шамасы әр уақытта оң және параметрдің
мәні өскенде бұл функция монотонды
өспелі екендігін байқаймыз, демек,
қисықтың нүктесі мен доғаның ұзындығының
арасында бір мәнді үздіксіз сәйкестік
бар. Қисықтың бастапқы нүктесінің әр
түрлі жақтарында жатқан нүктелер үщін
параметрдің әр түрлі мәндері сейкес.
Осы себепті s шамасын доғаның параметрі
ретінде қабылдауға болады және бұл
қисықтың табиғи (натурал) параметрі деп
аталады. Кез келген t параметрі бойынша
алынғын туындыдан айырмашылық болу
үшін, табиғи s параметрі бойынша алынған
туындны нүктемен белгілейміз, сонымен:
шамасы әр уақытта оң және параметрдің
мәні өскенде бұл функция монотонды
өспелі екендігін байқаймыз, демек,
қисықтың нүктесі мен доғаның ұзындығының
арасында бір мәнді үздіксіз сәйкестік
бар. Қисықтың бастапқы нүктесінің әр
түрлі жақтарында жатқан нүктелер үщін
параметрдің әр түрлі мәндері сейкес.
Осы себепті s шамасын доғаның параметрі
ретінде қабылдауға болады және бұл
қисықтың табиғи (натурал) параметрі деп
аталады. Кез келген t параметрі бойынша
алынғын туындыдан айырмашылық болу
үшін, табиғи s параметрі бойынша алынған
туындны нүктемен белгілейміз, сонымен:
 ,
,

(2) формуладан:
ds= dt
dt
бұдан
ds= =
=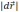 (3)
(3)
немесе
 =
= =1.
(4)
=1.
(4)
Тұжырым:
қисықтың нүктесінің радиус-векторынан
натурал s параметрі бойынша алынған
 бірінші туынды – вектор қисықтың жанама
түзуінің бойымен бағытталған бірлік
вектор болады
S параметрі бойынша
екінші ретті туныдыны табамыз:
бірінші туынды – вектор қисықтың жанама
түзуінің бойымен бағытталған бірлік
вектор болады
S параметрі бойынша
екінші ретті туныдыны табамыз:
 =
=  .
.
 векторы
бірлік вектор (( 4) формуланы қараныз) ,
ал бірлік вектордың ұзындығы тұрақты
болғандықтан, бірінші лемма бойынша ,
екінші ретті
туынды векторы бірінші ретті
векторы
бірлік вектор (( 4) формуланы қараныз) ,
ал бірлік вектордың ұзындығы тұрақты
болғандықтан, бірінші лемма бойынша ,
екінші ретті
туынды векторы бірінші ретті  туынды векторына ортогональ:
туынды векторына ортогональ:

Бұдан векторы кеңістіктегі қисықтың қайсыбір нормаль түзуінің бағытталатынын байқаймыз.
Анықтама:
Бағыттаушы векторы  векторы болатын кеңістіктегі қисықтың
нормал түзуі қисықтың бас нормалы деп
аталады.
векторы болатын кеңістіктегі қисықтың
нормал түзуі қисықтың бас нормалы деп
аталады.
7 - Дәріс.
Тақырып. Жанасушы жазықтық
Кеңістікте қисықтың жанама түзуі арқылы өтетін кез келген жазықтық қисықтың жанама жазықтығы деп аталады.
Қисықтың бас нормалы арқылы өтетін жанама жазықтық қисықтың жанасушы жазықтығы деп аталады.
Кеңістіктегі қисық параметрлік теңдеулерімен берілгенде қисықтың жанасушы жазықтығының теңдеуін табу үшін туындыларды табуда параметрлік теңдеумен берілген қисықтың нүктесінің радиус-векторының t параметрінен s параметріне көшу (түрлендіру ) формуласын білу қажет, осы себепті
 (1)
(1)
Теңдеуінен t параметрі бойынша бірінші және екінші туындыларды есептейміз.
 (2)
(2)

 (3)
(3)
Біз (3)
формуладан  векторы
векторы  және
және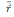 векторлары анықтайтын жазықтыққа
тиісті екекндігін байқаймыз, олай болса
,
векторлары анықтайтын жазықтыққа
тиісті екекндігін байқаймыз, олай болса
, және
векторлары жанасушы жазықтыққа тиісті.
және
векторлары жанасушы жазықтыққа тиісті.
Векторлардың
векторлық көбейтіндісінің қасиеті
бойынша  =
=
 векторы жанасушы жазықтыққа перпендикуляр
болатыны белгі себебі,
векторы жанасушы жазықтыққа перпендикуляр
болатыны белгі себебі,
 ,
,  ⊥
⊥
 .
.
Жанасушы
жазықтықтың теңдеуін жазамыз. Егер
 векторы жанасушы жазықтықтың ағымды
нүктесінің радиус-векторы болса, онда
векторы жанасушы жазықтыққа тиісті
екендігі түсінікті, олай болса,
-
векторы жанасушы жазықтықтың ағымды
нүктесінің радиус-векторы болса, онда
векторы жанасушы жазықтыққа тиісті
екендігі түсінікті, олай болса,
-  ,
,  векторлары
компланар, демек, бұл векторлардың
аралас көбейтіндісі нольге тең:
векторлары
компланар, демек, бұл векторлардың
аралас көбейтіндісі нольге тең:
(
- 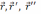 )
= 0 (4)
)
= 0 (4)
(4) формула жанасушы жазықтықтың теңдеуі. Егер векторының координаталары (ξ,η,ζ) болса, онда үш вектордың компланарлық шартын, демек, (4) формуланы осы векторлардың координаталары арқылы былайша жазамыз:
 = 0, (5)
= 0, (5)

 =
=  векторы нөлдік вектор болатын қисықтың
нүктелері үшін (5 ), не болмаса (4) формула
мәнін жояды.
векторы нөлдік вектор болатын қисықтың
нүктелері үшін (5 ), не болмаса (4) формула
мәнін жояды.  .
Векторы нөлдік вектор болатын қисықтың
нүктелері қисықтың түзелуші нүктелері
деп аталады. Түзелуші нүктелерде жанасушы
жазықтық анықталмайды.
.
Векторы нөлдік вектор болатын қисықтың
нүктелері қисықтың түзелуші нүктелері
деп аталады. Түзелуші нүктелерде жанасушы
жазықтық анықталмайды.
Мысал. Винттік x=a cos u, y= a sin u, z= bu сызығының жанасушы жазықтығының теңдеуін жазайық.
Винттік сызықтық теңдеуінен:
x'= - a sin u, y'= a cos u, z'=b;
x''= - a cos u, y''= - a sin u, z''=0.
(2) формулада ε,ζ,η айнымалыларының орнына x,y,z айнымалыларын енгізсек, (2) формула былай жазылады:

Бұдан
xb sinu – ybcosu + az – abu = 0.
Бұл винттік сызықтың жанасушы жазықтығының теңдеуі.
8 - Дәріс
Тақырып. Қисықтың серіктес үшжағы
