2. Кодовые таблицы

При вводе информации каждый символ (буквы, цифры, знаки пунктуации и др.) кодируются определенной последовательностью двоичных цифр в соответствии с международными стандартами кодирования, которые называются таблицами кодирования.

Наиболее широкое распространение имеет кодовая таблица ASCII (American Standard Code for Information Interchange). В первой части таблицы (коды 0-127) содержаться коды латинских букв, цифр, знаков препинания и управляющих символов. Вторая часть таблицы (коды 128-255) предназначена для размещения символов национального алфавита. В разных странах, в разных операционных системах могут использоваться различные варианты второй половины кодовой таблицы, их называют расширениями ASCII.

Система кодировки Unicode предназначена для поддержки символов национального алфавита. Набор знаков в кодировке Unicode имеет несколько форм представления. В большинстве случаев используется двухбайтная кодировка, что позволяет закодировать 65536 символов.

3. Кодирование растровых изображений

Растровое изображение формируется из множества отдельных точек (пикселей). Каждая точка характеризуется положением и цветом.

Глубина цвета – это число разрядов, отводимых для кодирования цвета каждой точки, т.е. количество битов на один пиксель. Глубина цвета измеряется в битах.

Черно-белые штриховые изображения кодируются одним битом. Для кодирования 256 полутонов оттенков серого цвета требуется 1 байт – этот формат кодирования черно-белых изображений является в настоящее время общепринятым.

Для кодировки растра цветного изображения используются различные стандарты кодировки:

Стандарт 256 цветов (1 байт) позволяет кодировать 256 оттенков цвета.

Стандарт High Color (2 байта) позволяет кодировать до 65 тыс. цветовых оттенков.

Стандарт True Color (3 байта) позволяет кодировать 16,7 млн. различных цветов. Этот формат в своей основе имеет три основных цвета: красный (Red, R), зеленый (Green, G) и синий (Blue, B). Каждый цвет имеет 256 оттенков и кодируется 1 байтом. В результате смешения трех основных цветов получается 16,7 млн. оттенков. Такая система кодирования называется RGB по первым буквам названий основных цветов.

6. Основные понятия алгебры логики

   1. Алгебра высказываний

Высказывание – это повествовательное предложение, которое либо истинно, либо ложно. В высказывании говорится о единственном событии. Высказывание «Москва – столица России» является истинным, а высказывание «Волга впадает в Черное море» - ложным.

Не всякое предложение является высказыванием. К высказываниям не относятся вопросительные и восклицательные предложения; предложения, в которых не может быть единого мнения о том, истинны они или ложны.

Из двух предложений можно образовать новые предложения с помощью союзов: «И», «ИЛИ», «ЕСЛИ… ТО…», «ТОГДА И ТОЛЬКО ТОГДА, КОГДА», также с помощью частицы «НЕ» или словосочетания «НЕВЕРНО, ЧТО», которые в алгебре высказываний называются логическими связками.

Высказывания обозначаются большими буквами латинского алфавита. Высказывания принимают значения «истина» (1) или «ложь» (0).

В алгебре высказываний определены действия над высказываниями, в результате выполнения которых получают новые высказывания.

Пусть А и В простые высказывания.

Инверсией (отрицанием) называется логическая операция, проводимая с одним высказыванием, с помощью связки «НЕ ВЕРНО, ЧТО». Обозначения инверсии: 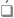(подчеркивание сверху), NOT, НЕ. А читается, как «неверно, что А».

Конъюнкцией (логическим умножением) называется операция объединения простых высказываний в одно с помощью союза «И». Обозначения конъюнкции: *, , &, AND, И. А & В читается, как «А и В».

Дизъюнкцией (логическим сложением) называется операция объединения простых высказываний в одно с помощью союза ИЛИ. Обозначение дизъюнкции6 +, , OR, ИЛИ. А  В читается, как «А или В».

Импликацией (логическим следованием) называется операция объединения двух простых высказываний в одно с помощью союза «ЕСЛИ …, ТО…». Обозначение импликации: . А  В читается, как «если А, то В» или «из А следует В».

Эквивалентностью (логическим равенством) называется операция объединения двух простых высказываний в одно с помощью союза «ТОГДА И ТОЛЬКО ТОГДА, КОГДА…». Обозначение эквивалентности: . А  В читается, как «А эквивалентно В тогда и только тогда, когда из А следует В и из В следует А».

Неэквивалентностью (логическим неравенством, исключающим ИЛИ) называется операция объединения двух простых высказываний в одно с помощью союза «ТОГДА и ТОЛЬКО ТОГДА, КОГДА…». Обозначения: , XOR. А  В читается, как «А не эквивалентно В тогда и только тогда, когда из А не следует В, а из В не следует А».

При определении значения логического выражения учитывают старшинство или приоритет логических операций: сначала выполняется инверсия, затем конъюнкция, а потом дизъюнкция. Для изменения указанного порядка используют скобки.

2. Таблица истинности

Высказывания, образованные при помощи операций логического сложения, умножения и отрицания, называют сложными высказываниями. Истинность всякого сложного высказывания устанавливают с помощью таблиц истинности (табл. 1.1), которые содержат всевозможные комбинации значений входных переменных вместе с соответствующими им значениями выходных переменных.

Таблица 1.1

		Инверсия	Конъюнкция	Дизъюнкция	Импликация	Эквива-лентность	Неэкви-валентность
		Отрицание	Умножение	Сложение	Следование	Равенство	Неравенство
		NOT	AND & *	OR +			XOR
А	В		А  В	А  В	А  В	А  В	А  В
0	0	1	0	0	1	1	0
0	1	1	0	1	1	0	1
1	0	0	0	1	0	0	1
1	1	0	1	1	1	1	0

Например, истинность высказывания F=A&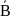 можно установить с помощью таблицы истинности 1.2.

Таблица 1.2

А	В		A&
0	0	1	0
0	1	0	0
1	0	1	1
1	1	0	0