1.2. Приведение транспортной задачи к правильному балансу

Возможны две ситуации – избыток или дефицит продукта

1. Избыток продукта .

В этом случае вводится дополнительный фиктивный пункт назначения B_m+1, в котором якобы имеются потребности b_m+1 на избыточный продукт в количестве . Так как перевозки являются фиктивными и производиться не будут, затраты на них равны нулю (c_i,m+1= 0, 1  i  n). Задача становится сбалансированной и может решаться обычными методами.

Результаты решения такой задачи должны интерпретироваться следующим образом. Перевозки х_i,m+1, 1  i  n являются фиктивными, эти объёмы грузов вывезены не будут. В оптимальном плане перевозок не будет вывезена часть грузов из пунктов отправления, откуда перевозки окажутся наиболее дорогими. В условиях рыночной экономики это означает, что поставщики должны либо искать новых заказчиков в более близком регионе, либо переводить производство на более востребованную продукцию.

2. Дефицит продукта .

Здесь возможно несколько стратегий приведения задачи к правильному балансу.

2.1. При отсутствии каких-либо ограничений вводится дополнительный фиктивный пункт отправления А_n+1, в котором якобы имеются запасы а_n+1 недостающего продукта в количестве 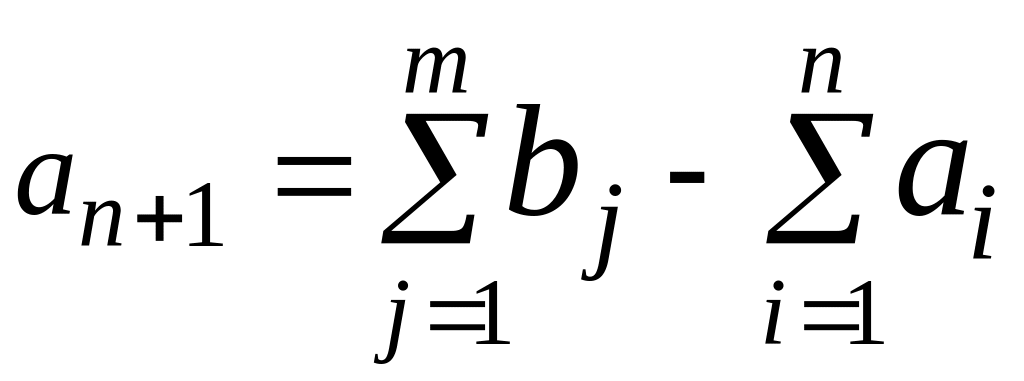. Так как перевозки являются фиктивными и производиться не будут, затраты на них равны нулю (c_n+1,j= 0, 1  j  m). Задача становится сбалансированной и может решаться обычными методами.

Результаты такого решения должны интерпретироваться следующим образом. Перевозки х_n+1,j, 1  j  m являются фиктивными, эти объёмы грузов доставлены не будут. В оптимальном плане перевозок не будет доставлена часть грузов в пункты назначения, куда перевозки окажутся наиболее дорогими. В условиях рыночной экономики это означает, что заказчики должны либо искать новых поставщиков в более близком регионе, либо ограничивать свои потребности на данный продукт.

2.2. Продукт имеет важное социальное или стратегическое значение и других поставщиков этого продукта в близлежащем регионе нет. В этом случае нельзя оставить часть потребителей вообще без продукта и обычно просто все заявки пропорционально уменьшают. Вводится коэффициент  пропорционального уменьшения заявок , и все заявки корректируются в сторону уменьшения b_j^* = b_j, где b_j^* - скорректированные объёмы заявок.

Примечание: скорректированные объёмы заявок должны быть округлены таким образом, чтобы выполнялось балансное условие (5).

Данная стратегия может применяться только при условии, что потребности рассчитываются объективно, либо в условиях рыночной экономики заявки регулируются ценами на продукт, иначе такая стратегия приводит к лавинообразному возрастанию дефицитов.

2.3. Все пункты отправления и пункты назначения принадлежат одной фирме. Тогда можно найти более эффективное решение. Как и в п. 2.1. вводится дополнительный фиктивный пункт отправления А_n+1, в котором якобы имеются запасы а_n+1 недостающего продукта в количестве

.

Только вместо затрат на перевозки в качестве c_n+1,j, 1  j  m используют потери от недопоставки единицы продукта в пункт назначения B_m+1. В этом случае целевая функция представляет собой сумму транспортных издержек и потерь от недопоставки грузов.

Результаты такого решения должны интерпретироваться следующим образом. Перевозки х_n+1,j, 1  j  m являются фиктивными, эти объёмы грузов доставлены не будут. В оптимальном плане перевозок не будет доставлена часть грузов в те пункты назначения, куда, во-первых, перевозки окажутся наиболее дорогими и, во-вторых, где потери от недопоставки продуктов будут минимальны.