Обчислення визначених інтегралів функції комплексної змінної за допомогою лишків.
Нехай
точка
-
ізольована особлива точка функції
.
Тоді лишком функції
в точці
називається
число
,
рівне інтегралу
,
де
- коло
з центром в точці
достатньо малого радіусу, що міститься
всередині області аналітичності функції
і не має в собі інших особливих точок.
З означення лишка функції
випливає, що
,
де
-
коефіцієнт при мінус першому степені
лоранівського розкладення функції
в околі
.
Якщо
-
усувна особлива точка, то
.
Якщо
- полюс
n-го
порядку функції
,
то
Теорема Коші:
Якщо
функція
аналітична на границі Г області D
і
всередині області D,
за винятком скінченного числа особливих
точок
,
то
.
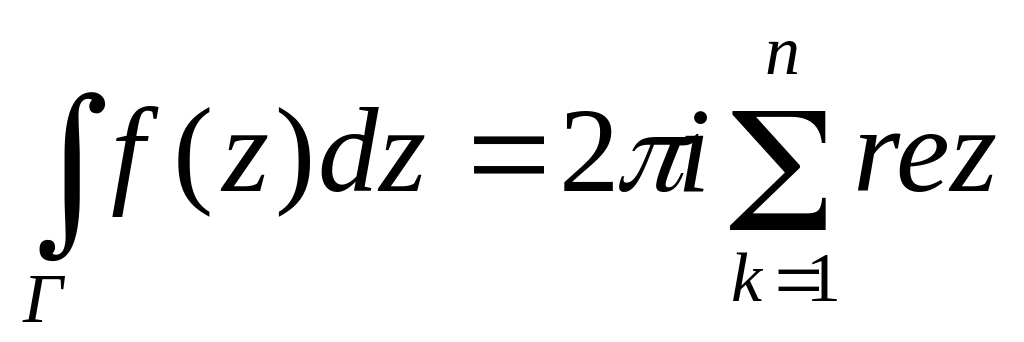
1.
Обчислити
,
де Г – мале коло, яке оточує початок
координат.
Розв’язок:
Маємо - полюс 2-го порядку, бо для малих виконується:
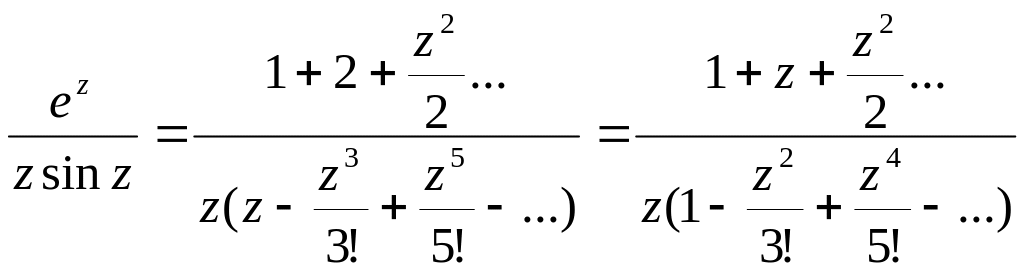
2.
Обчислити
Розв’язок:
Заміна
перетвоює в площині
відрізок
в коло
.
Маємо
,
Тоді
.
Особливі
точки
-
прості полюса, причому
всередині контура С.
Маємо:
.
Обчислюємо
,
,
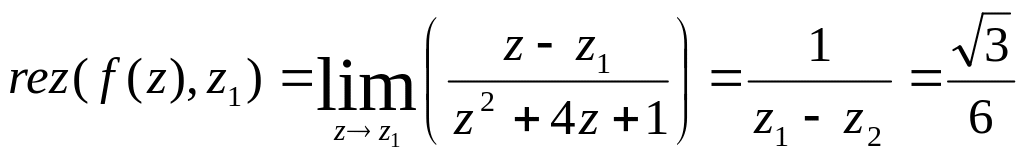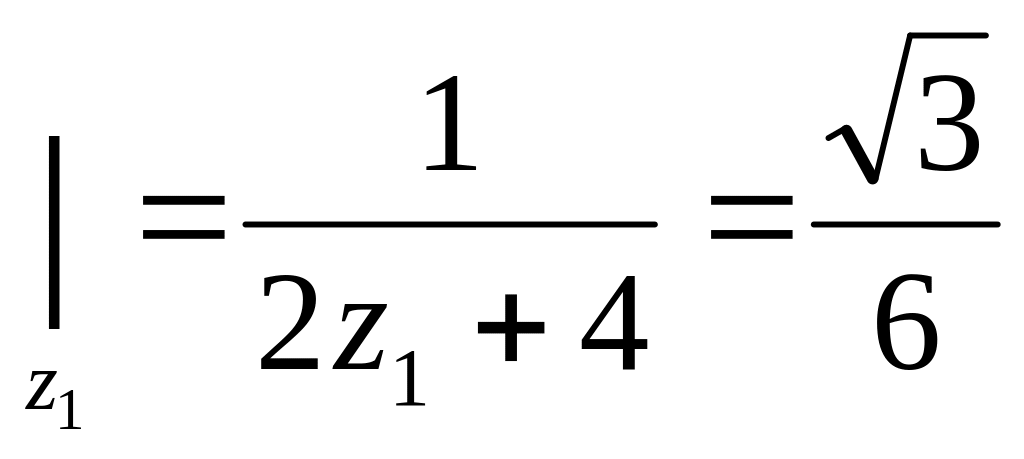і
.
Лекція 15
Обчислення деяких невласних інтегралів за допомогою лишків.
Обчислити
Розв’язок:
Якщо
функція
має нескінченно віддалену точку
нулем другого або вищого порядку, то
.
-
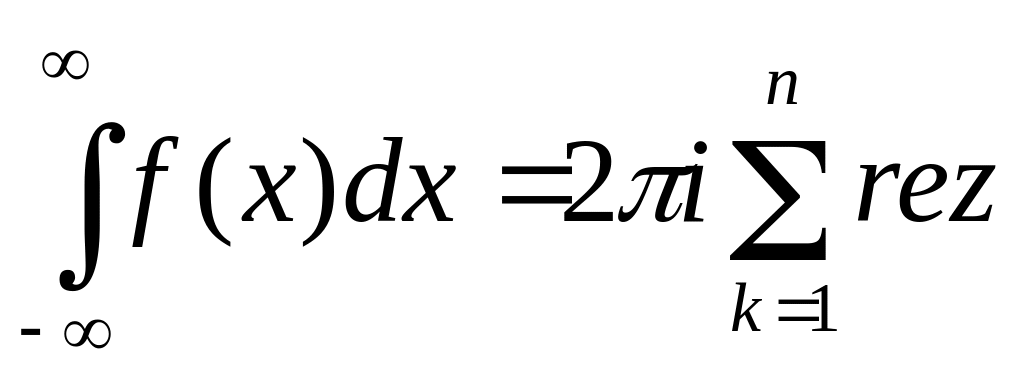
особливі точки функції
,
такі що
.
Функція
має точку
,
нулем 3-го порядку; її особливі точки,
полюси 2-го порядку, знаходимо із рівняння
,
при чому
.
Тоді
.
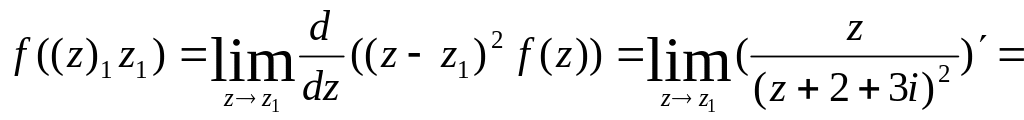
Маємо
.
Варіанти індивідуальних завдань.
1.
Записати дане комплексне число
в тригонометричній та показниковій
формах. Побудувати його на площині і
знайти комплексно-спряжене число
.
Виконати для числа дії:
а)
,
,
;
б)
,
,
,
,
,
;
в)
,
,
,
;
г)
,
,
;
2. На площині побудувати геометричне місце точок для заданих співвідношень.
3. Обчислити.
4. Розв’язати рівняння.
5. Довести диференційовність функції і знайти її похідну.
6. Знайти
коефіцієнт розтягу
,
і кут повороту
в точці
функції
.
7. Знайти
аналітичну функцію
по заданій дійсній або уявній частині
та умові
.
8. Обчислити.
9. Розкласти аналітичну функцію в ряд:
а)
Тейлора по ступеням
,
використовуючи розвинення функції в
ряд по ступеням
і знайти радіус збіжності.
б)
Лорана, в околі точки
в кільці
,
.
10. Обчислити інтеграли за допомогою лишків.
Варіант 1. Варіант 2.
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
1.
2.
,
3.
4.
5.
6.
7.
8.
9.
10.
|
,
,
,
,
,
,
,
,
,
,
.
;
;
;
.
.
,
,
.
.
,
,
.
,
,
.
,
;
.
,
,
,
,
,
,
,
,
,
,
,
,
.
;
;
.
.
.
,
,
.
.
,
початкова
точка інтегрування с
,
,
.
,
;
.
Варіант 3. Варіант 4.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
1.
2.
3. 4. .
5.
6.
7.
8.
9.
10.
|
,
,
,
,
,
,
,
,
,
,
,
,
,
,
.
;
;
.
,
,
.
,
.
,
,
,
.
.
,
;
.
,
,
,
,
,
,
,
,
,
,
,
,
,
.
;
;
.
.
,
,
.
.
,
,
,
.
,
;
.Варіант 5. Варіант 6.
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
1.
2.
3.
4.
5.
6.
7.
8.
;
9.
10.
|
,
,
,
,
,
,
,
,
,
,
,
,
,
.
;
;
.
.
.
,
,
.
.
;
,
,
,
.
,
;
.
,
,
,
,
,
,
,
,
,
,
,
,
,
.
;
;
.
.
.
,
,
.
.
відрізки
,
,
.
,
;
.
Варіант 7. Варіант 8.
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
1.
2.
3.
4.
5.
6.
7.
8.
;
відрізок
9.
10.
|
,
,
,
,
,
,
,
,
,
,
,
,
,
,
.
;
;
.
.
.
,
,
.
,
.
;
дуга
параболи
,
від точки
до
точки
,
,
.
,
;
.
,
,
,
,
,
,
,
,
,
,
,
,
,
,
.
;
;
.
.
.
,
,
.
,
.
,
,
.
,
.
Варіант 9. Варіант 10.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
,
,
,
,
,
,
,
,
,
,
,
,
,
,
.
;
;
.
.
.
,
,
.
,
.
;
по
,
,
,
,
.
,
,
,
.
,
,
,
,
,
,
,
,
,
,
,
,
,
,
.
;
;
.
.
.
,
,
.
.
;
на відрізку
.
,
,
.
,
,
,
.Варіант 11.+ Варіант 12+.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
1.
2.
3.
4.
5.
6.
,
7.
8.
Что за бред в методичке?
9.
10.
|
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
.
;
;
.
.
.
,
(мінус
перед „е”???),
.
,
(щось
не так.. не той знак: не „v”
а „w”).
;
на відрізку
.
,
,
.
;
,
.
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
.
;
;
.
.
.
,
.
,
.
,
,
.
,
,
.
;
,
.Варіант 13+. Варіант 14+.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
,
,
,
,
,
,
,
,
,
,
,
,
,
,
.
;
(??);
.
.
.
,
,
.
.
;
,
,
,
.
;
.
,
,
,
,
,
,
,
,
,
,
,
(В
числителе чехарда),
,
,
,
.
;
;
.
.
.
,
,
.
.
;
дуга
параболи
,
від
до
,
,
.
,
;
.Варіант 15+. Варіант 16+.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
1.
2.
3.
4.
5. .
6.
7.
8.
9.
10.
|
,
,
,
,
,
,
,
,
,
,
,
,
,
,
.
;
;
.
.
.
,
.
.
;
,
,
,
.
,
,
.
,
;
.
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
.
;
;
.
.
,
.
,
.
;
,
,
(
).
,
,
.
,
,
.
,
;
.Варіант 17+. Варіант 18+.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
1.
2.
.
3.
4.
5.
6.
7.
8.
9.
10.
|
,
,
,
,
,
,
,
,
,
,
,
,
,
,
.
;
;
.
.
.
,
.
,
;
,
,
.
,
,
.
,
;
.
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
;
;
.
.
.
,
.
.
;
по відрізку
,
.
,
,
.
,
;
.Варіант 19+. Варіант 20+.
1.
2.
3.
4.
5. .
6.
,
7.
8.
9.
10.
|
1.
2.
3.
4.
5. 6. , .
7.
8.
9. .
10.
|
,
,
,
,
,
,
,
,
,
,
,
,
,
,
.
;
;
.
.
.
.
,
по
відрізкам
.
,
,
.
.
,
;
.
,
,
,
,
,
,
,
,
,
,
,
,
,
,
.
;
;
.
.
.
,
.
,
на
відрізку
.
,
,
.
;
.Варіант 21+. Варіант 22+.
1.
2.
,
, .
3.
4.
5.
6.
,
7.
8.
9.
10.
|
1.
2.
3. 4. .
5.
6.
,
7.
8. ; по , .
9.
10.
|
,
,
,
,
,
,
,
,
,
,
,
,
,
;
;
.
.
.
,
,
.
;
по
,
.
,
,
.
,
;
.
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
.
;
;
.
.
.
,
,
.
,
;
.Варіант 23+. Варіант 24+.
1.
2.
,
3.
4.
5.
6.
,
7.
8.
9.
10. , ;
|
1.
2.
3.
4.
5.
6.
,
7.
8.
9.
10.
|
,
,
,
(в
методичцы лажа),
,
,
,
,
,
,
,
,
,
,
.
;
;
.
.
.
.
;
.
,
,
.
.
,
,
(в
методичцы лажа),
,
,
,
,
,
,
.
,
,
,
,
,
.
,
;
.
.
.
.
,
,
,
.
;
.Варіант 25+. Варіант 26+.
1.
2.
3.
4.
5. 6. ,
7.
,
8.
9.
10.
|
1.
2.
3.
4.
5. 6. ,
7.
8.
9.
10.
|
,
,
,
,
,
,
,
,
.
,
,
,
,
,
.
,
;
.
.
.
.
,
відрізок
,
,
.
.
,
;
.
,
,
,
,
,
,
,
,
.
,
.
,
,
,
.
,
;
.
.
.
.
,
відрізки
,
,
.
.
,
;
.Варіант 27+. Варіант 28+.
1.
2.
3.
4.
5.
6.
7.
8.
,
відрізок
9.
10.
|
1.
2.
3.
,
4. 5. .
6.
7. .
8.
9.
10.
|
,
,
,
,
,
,
,
,
.
,
.
,
,
,
.
,
;
.
.
.
,
.
прямої
.
,
,
.
.
,
;
.
,
,
,
,
,
,
,
.
,
,
,
,
,
.
;
.
.
,
.
,
,
.
,
,
.
,
;
.Варіант 29+. Варіант 30+.
|
1.
2.
3.
4.
5.
6.
,
7.
,
8.
9.
10.
|
1.
2.
3.
4.
5.
6.
,
7.
8.
9.
10.
|
,
,
,
,
,
,
,
,
,
.
,
,
,
,
,
.
,
;
.
.(что
за бред)
.
.
.
,
,
.
,
,
.
,
;
.
,
,
,
,
,
,
,
,
,
.
,
,
,
,
,
.
,
;
.
.
,
.
,
.
,
відрізки
.
,
,
.
,
,
.
;
.
Література:
В.А. Гончаров. Теорія функцій комплексної змінної. Учпедгіз. Москва, 1995.
І.Г. Араманович, Г.Л. Лунц, Л.Э. Эльзгольц. Избранные главы высшей математики для инженеров и студентов втузов. Изд. «Наука», Москва, 1968.
М.Л. Краснов, А.И. Киселев, Г.И. Макаренко. Избранные главы высшей математики для инженеров и студентов втузов. Задачи и упражнения. Изд. «Наука», Москва, 1971.
Данко П.Е., Попов А.Г. Высшая математика в упражнениях и задачах. Ч.Ш-М.:Высш. школа, 1971.
Анго Андре. Математика для электро- и радиоинженеров. – М.:Наука, 1966.
ВСЕ… хух=)
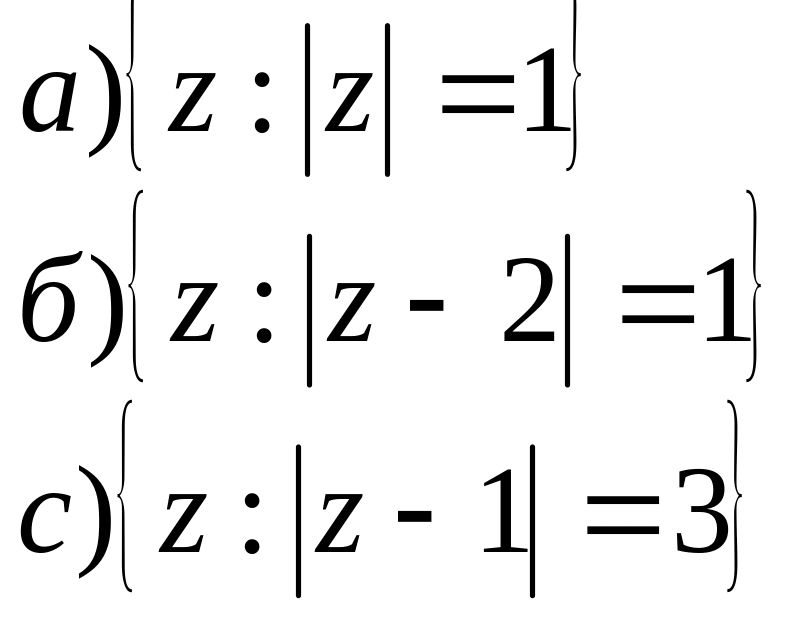
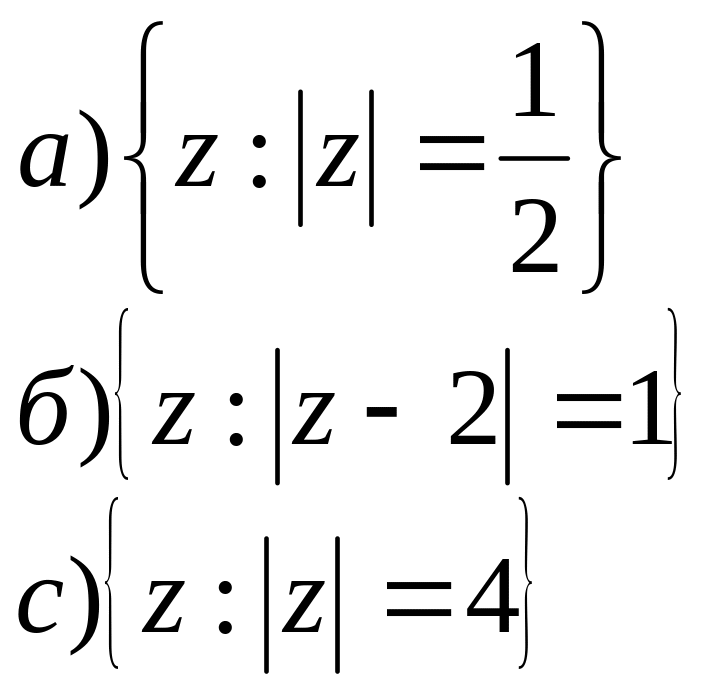
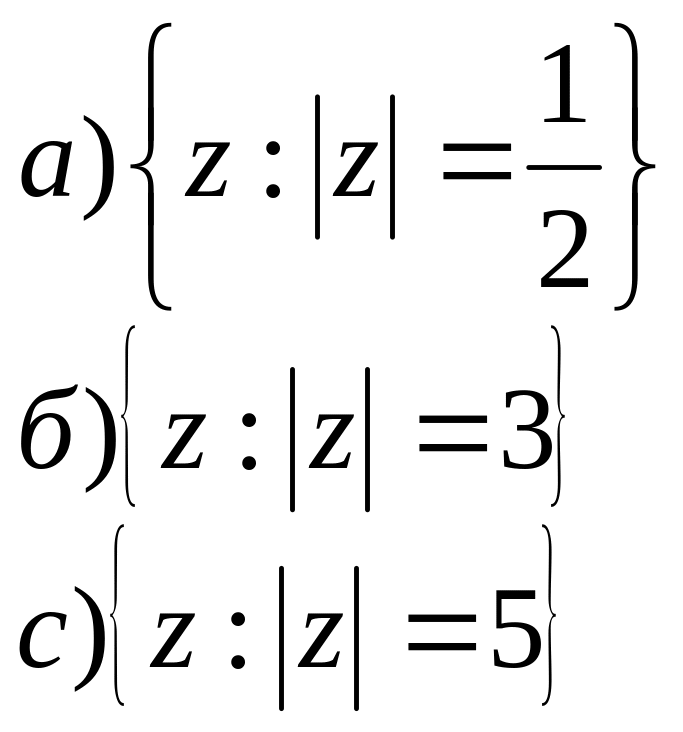
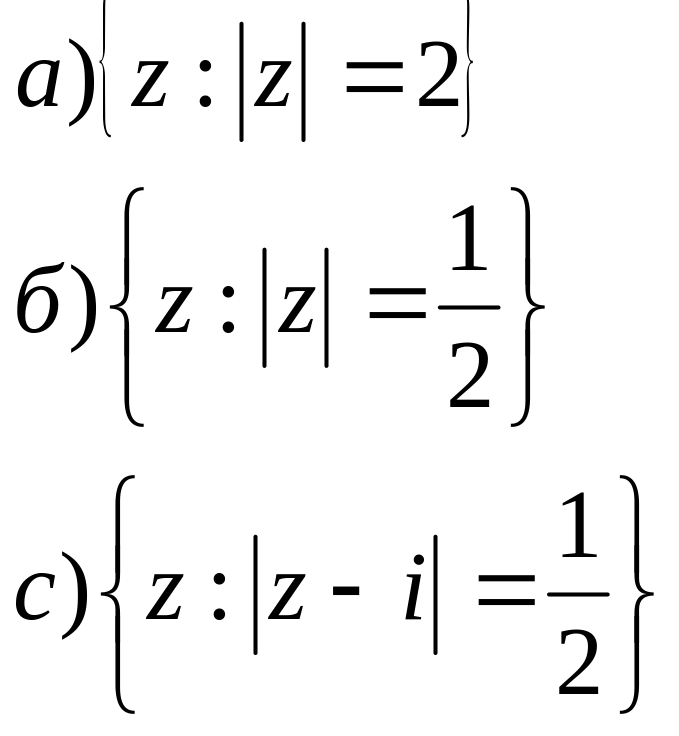
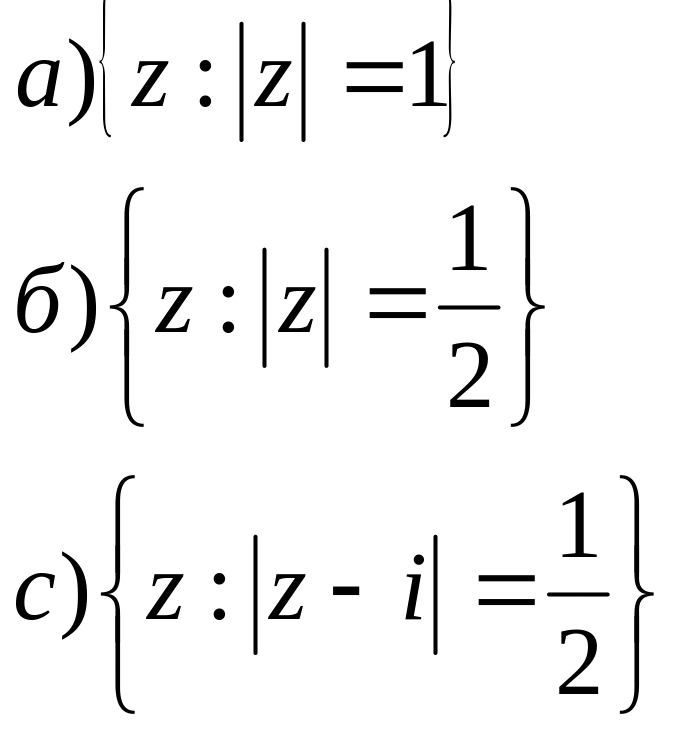
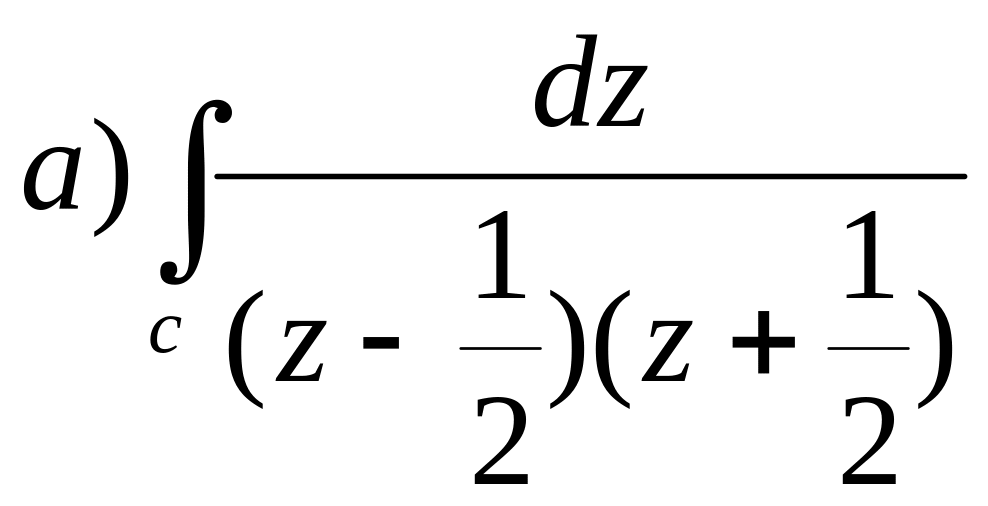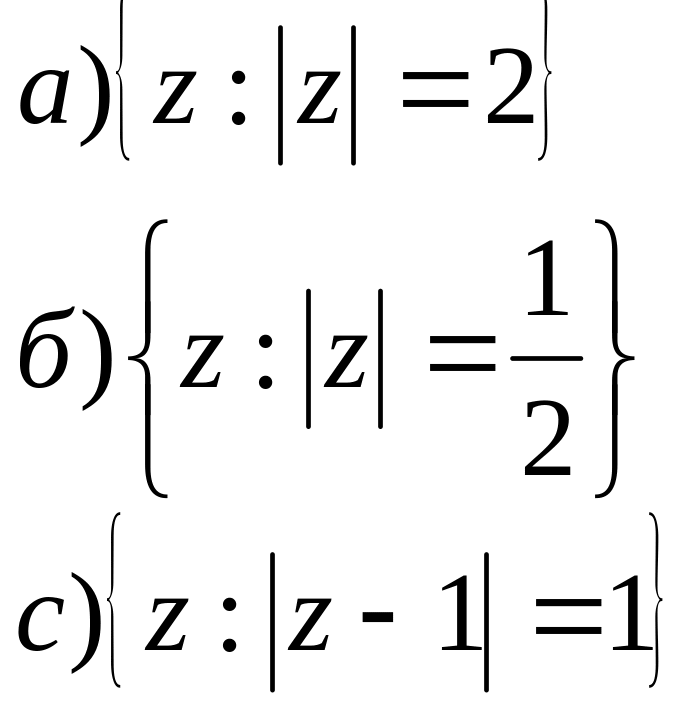
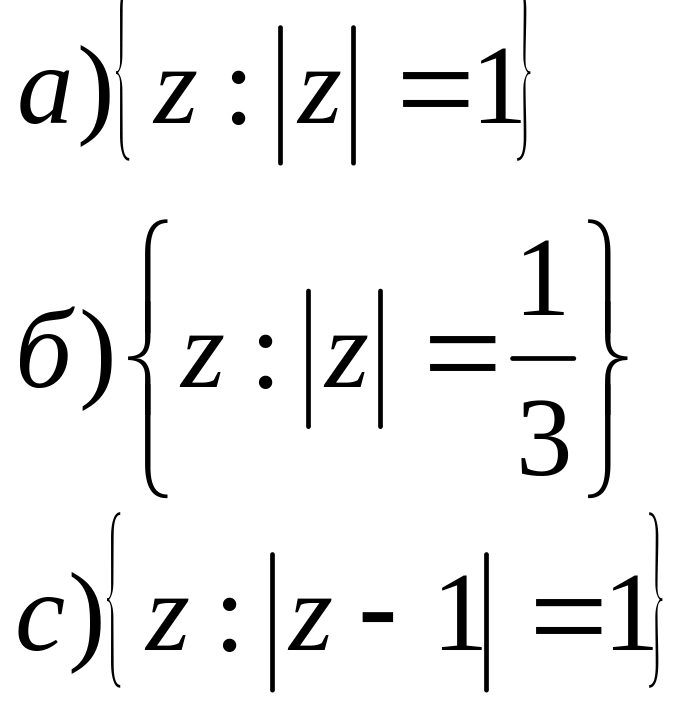
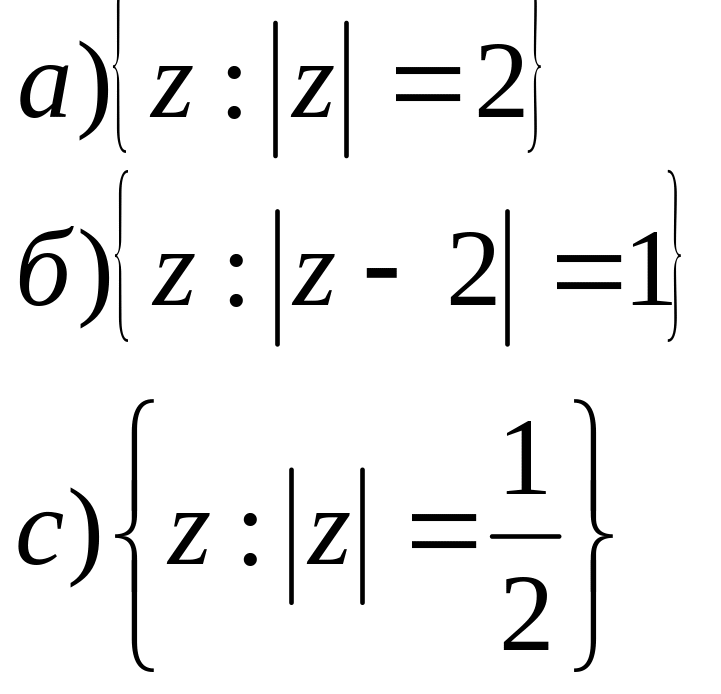
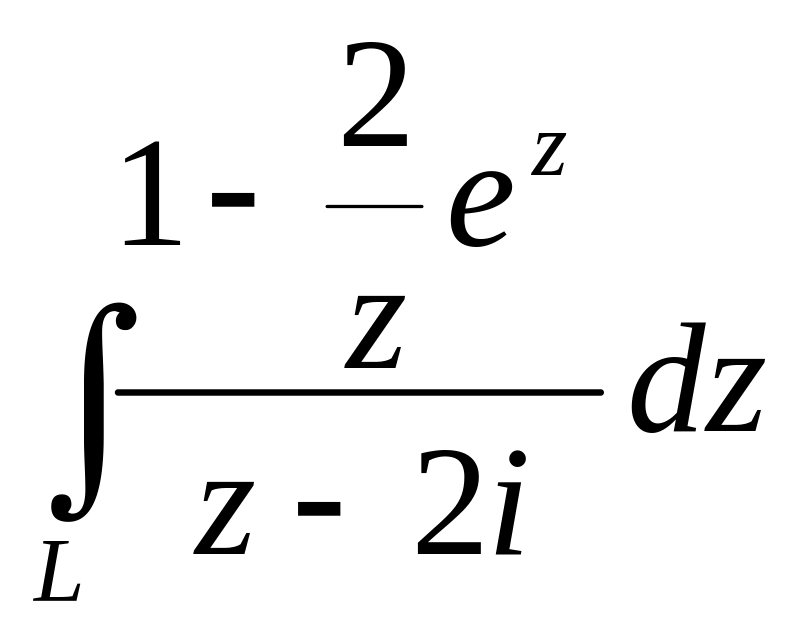
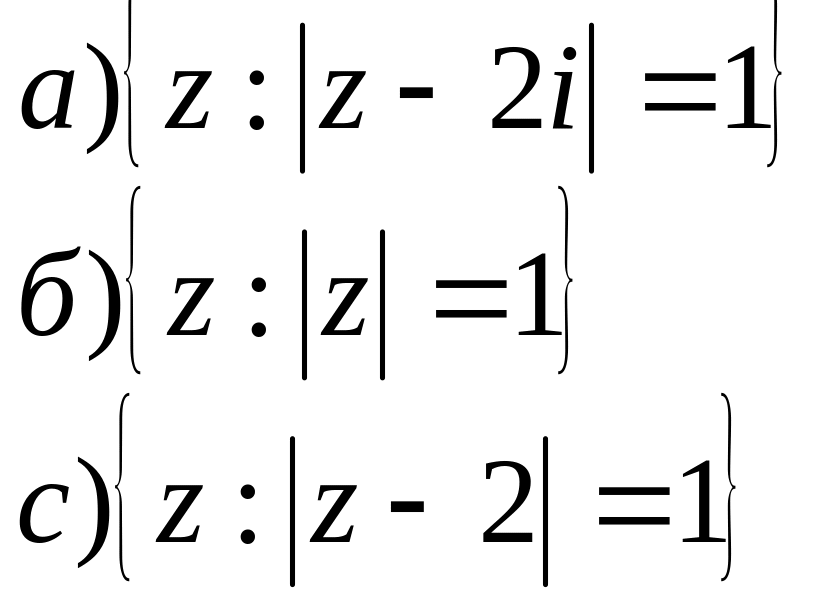
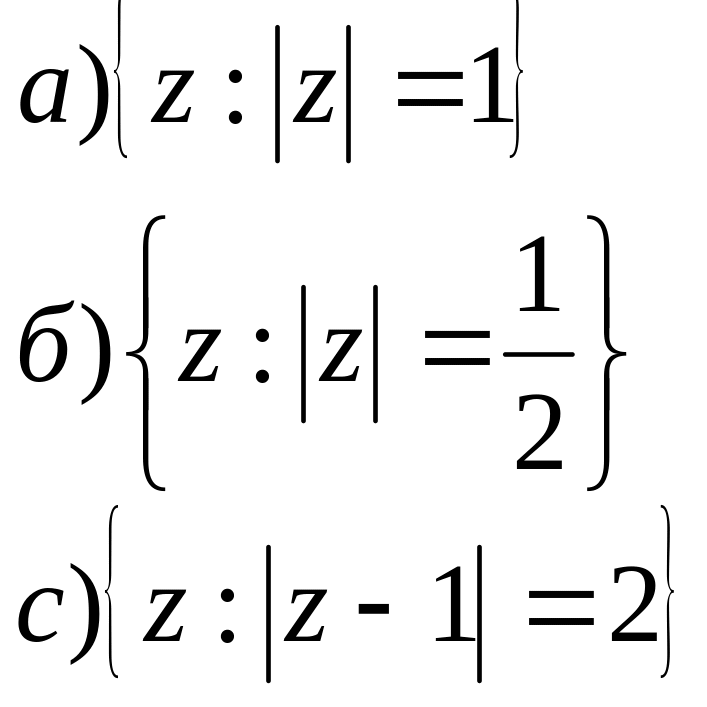
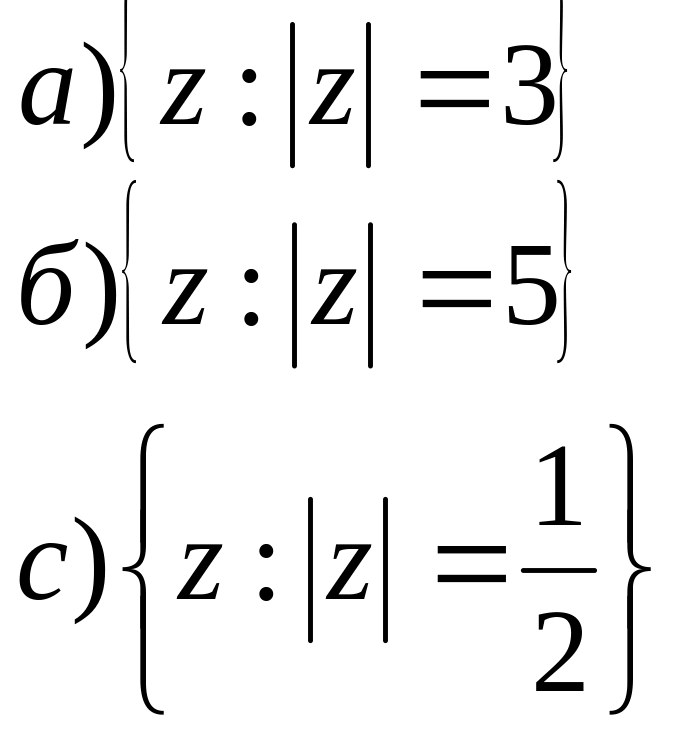
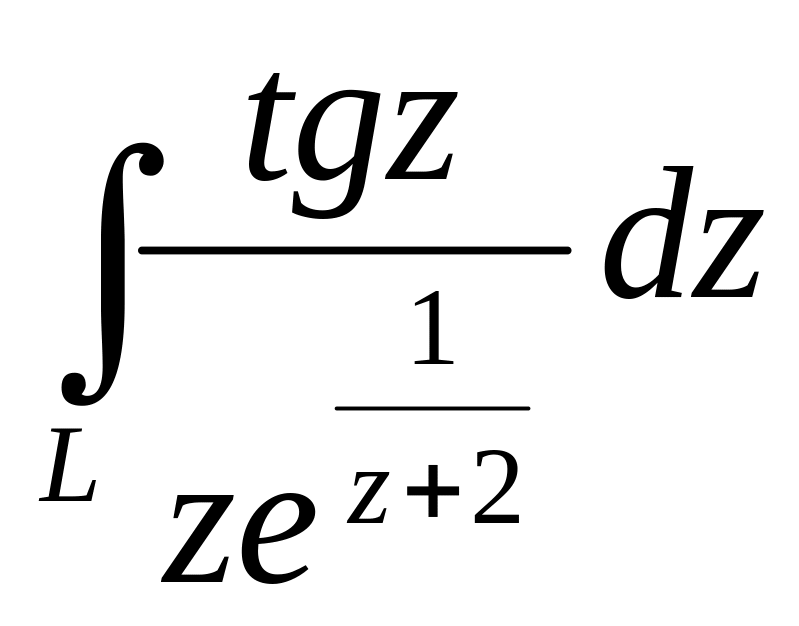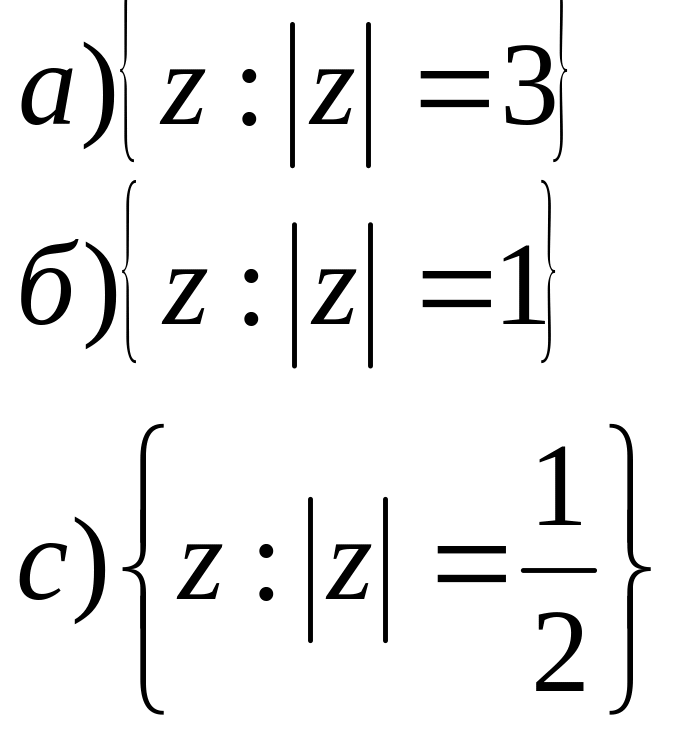
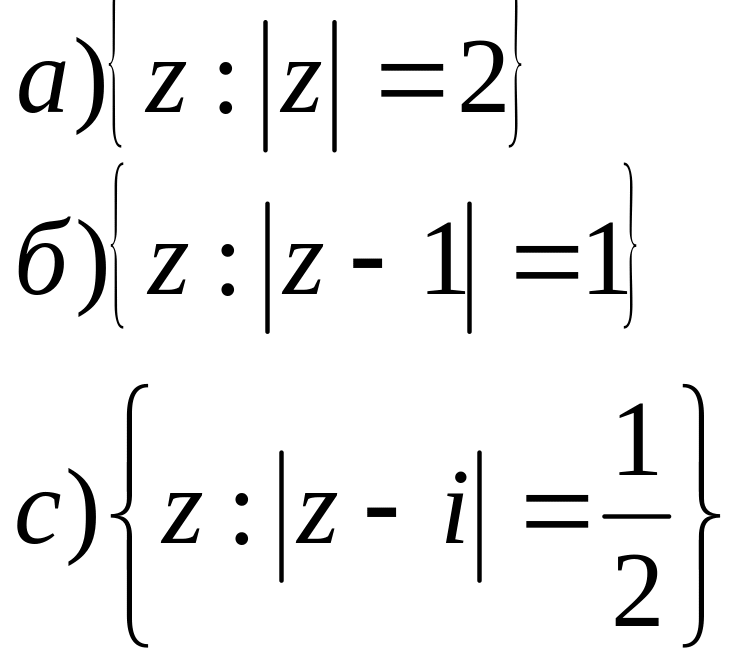
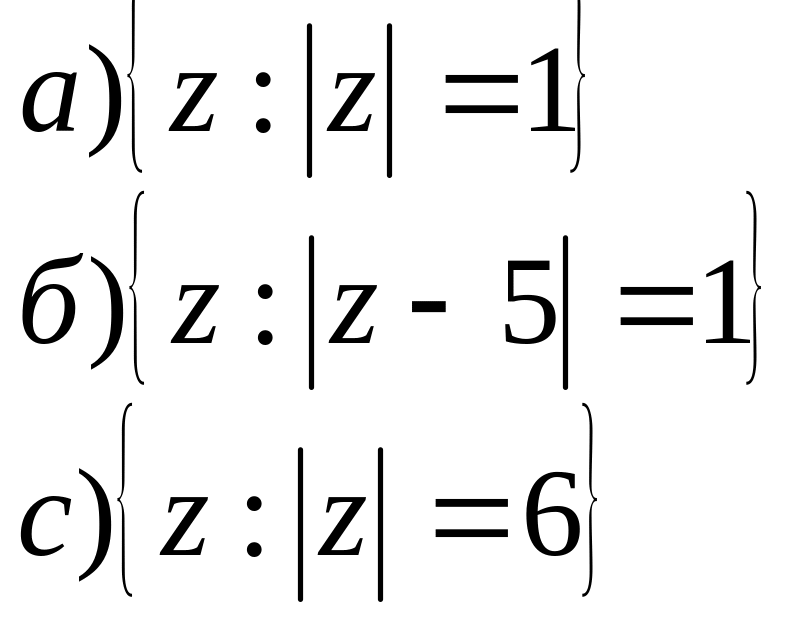
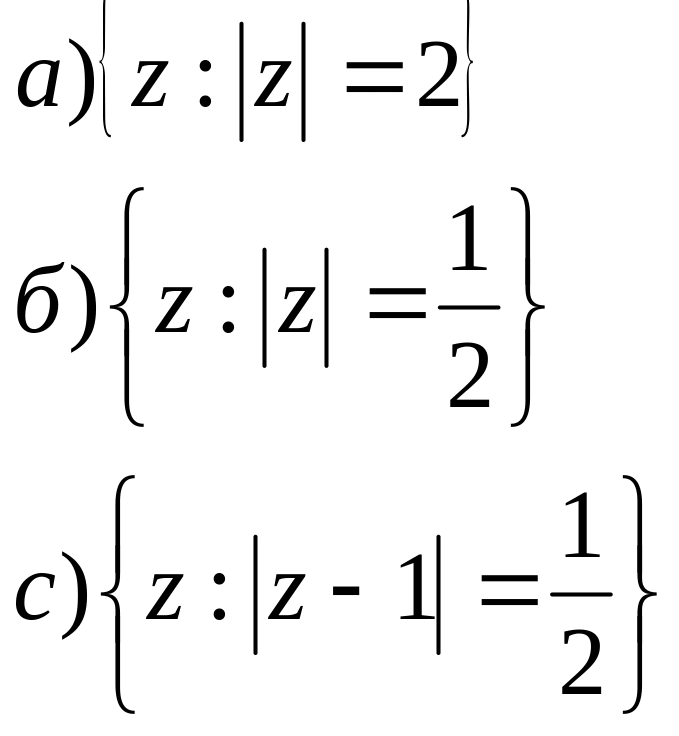
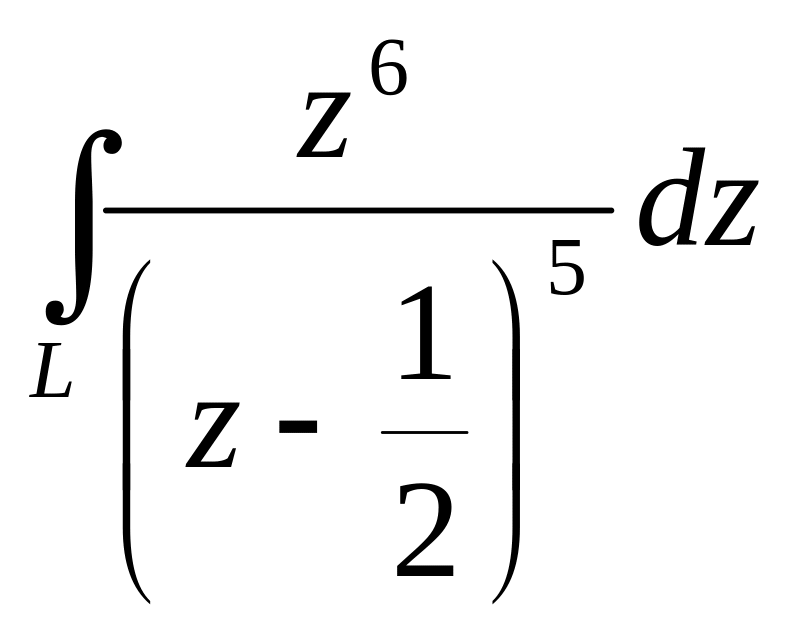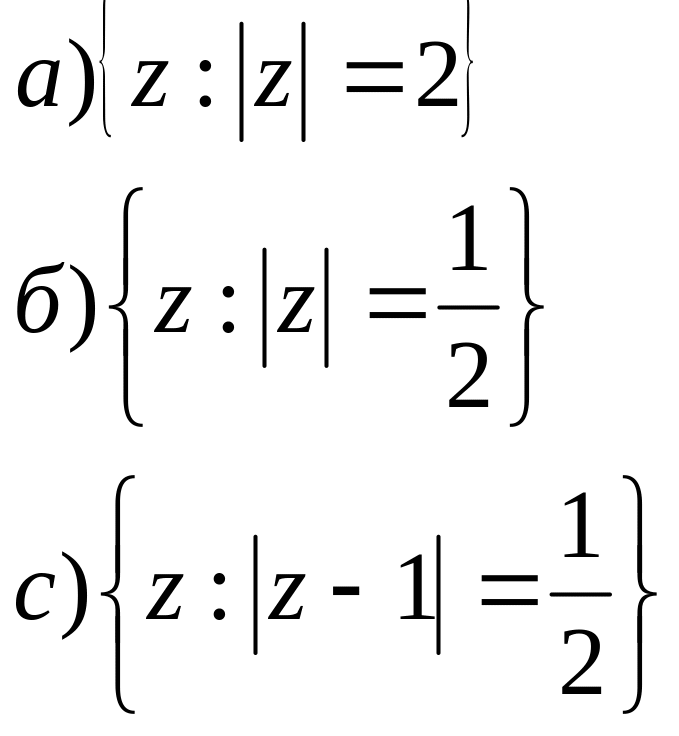
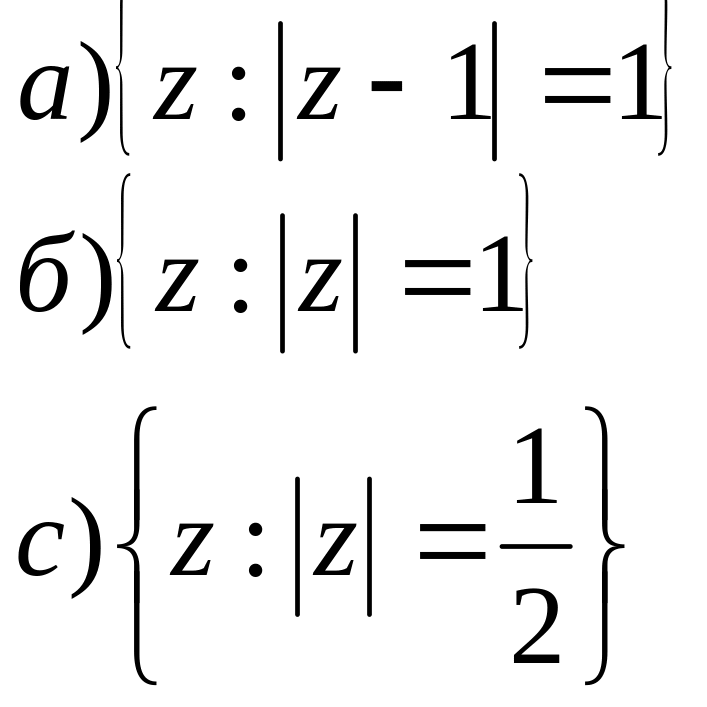
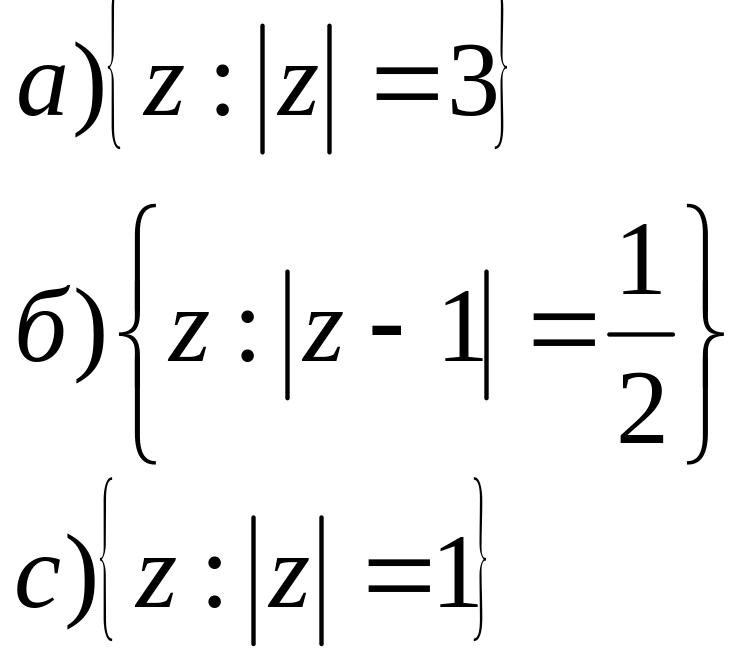
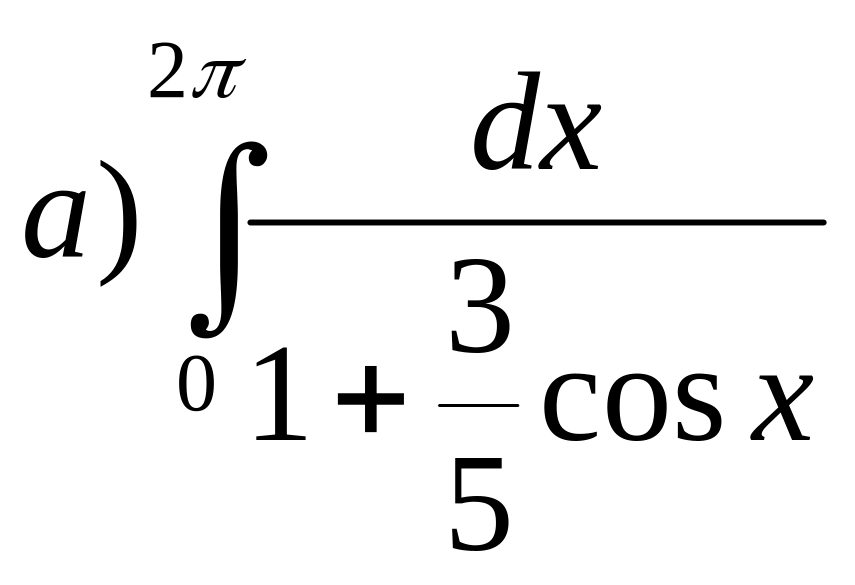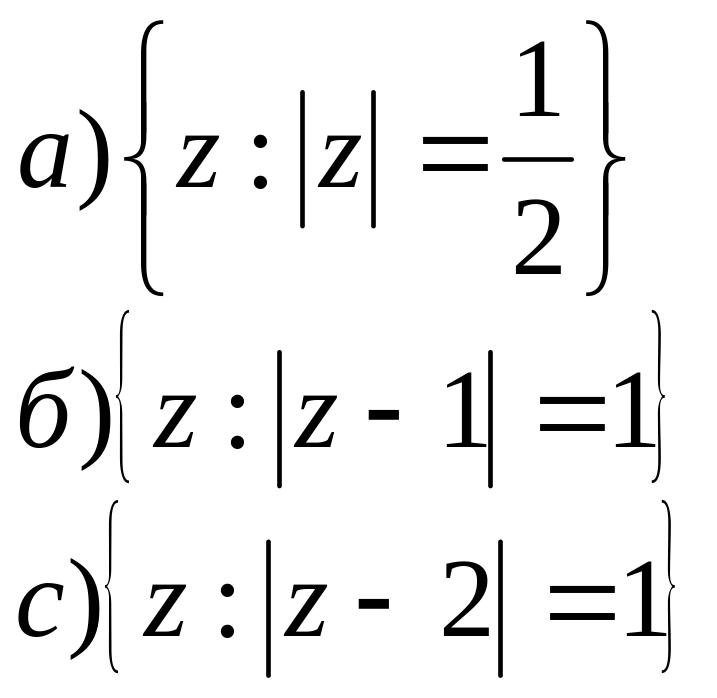
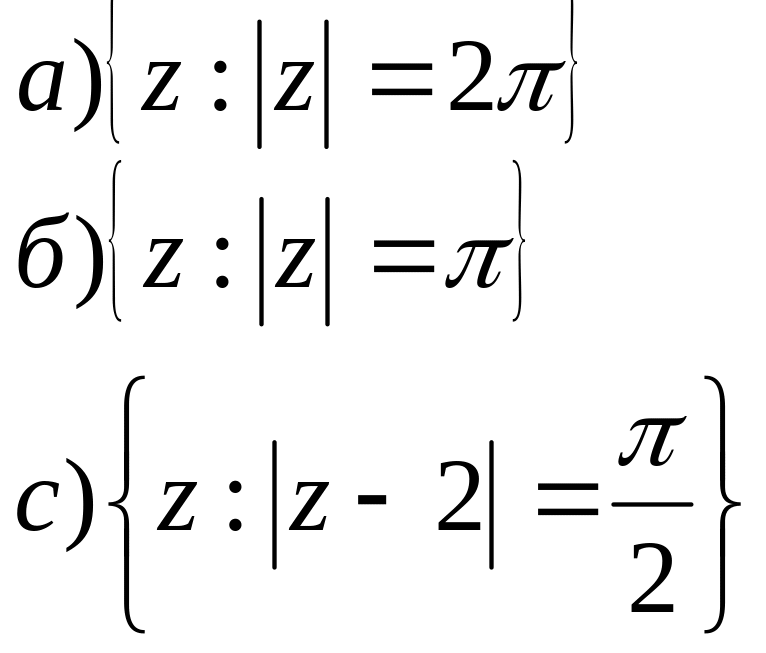
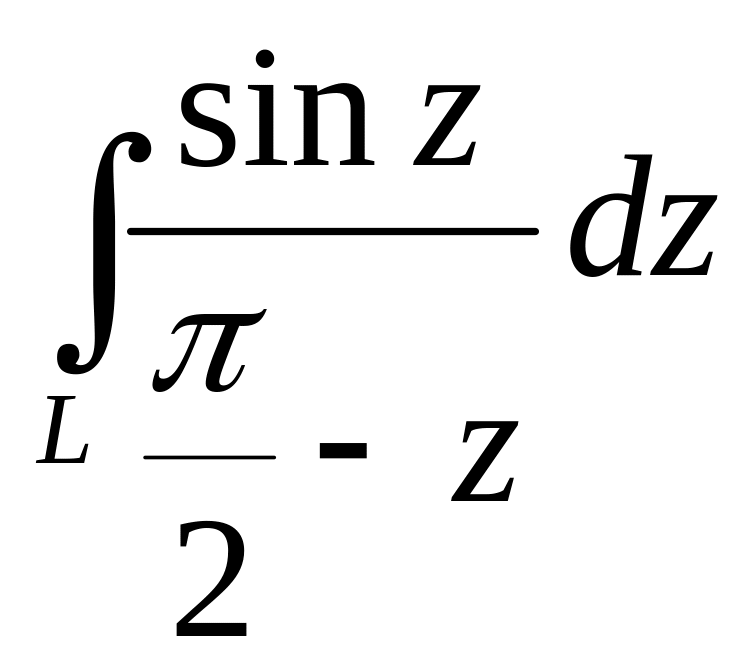
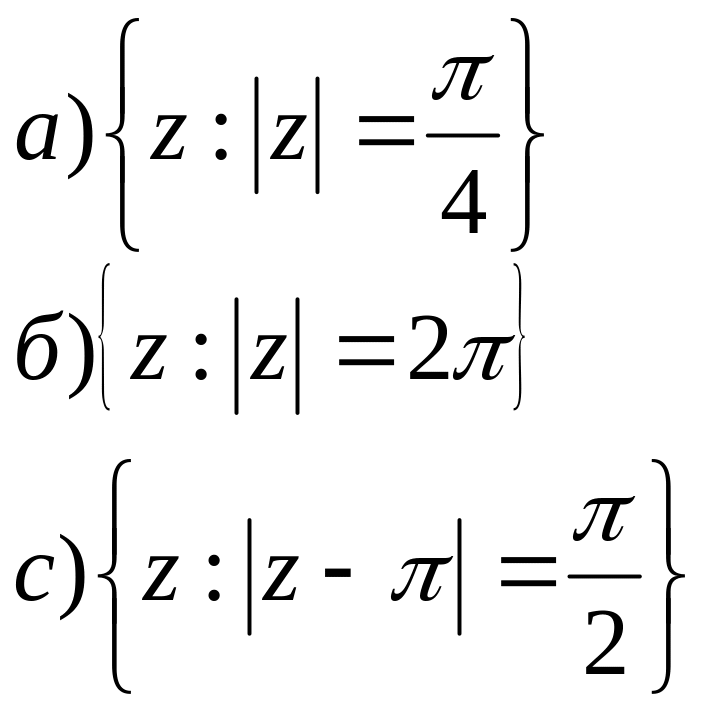
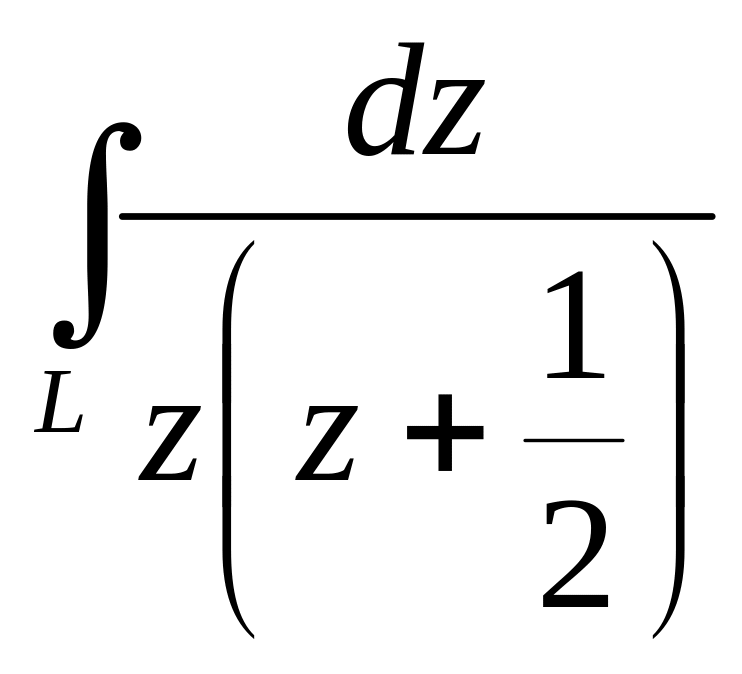
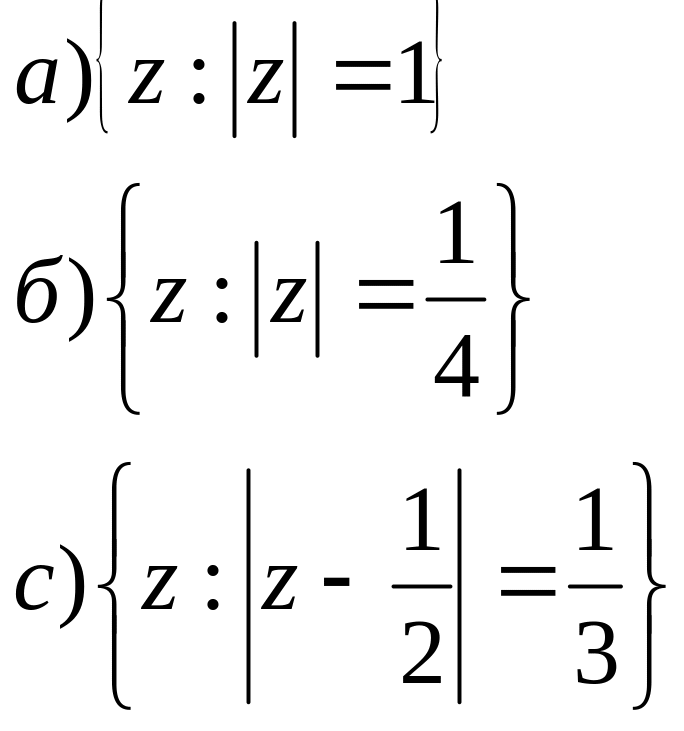
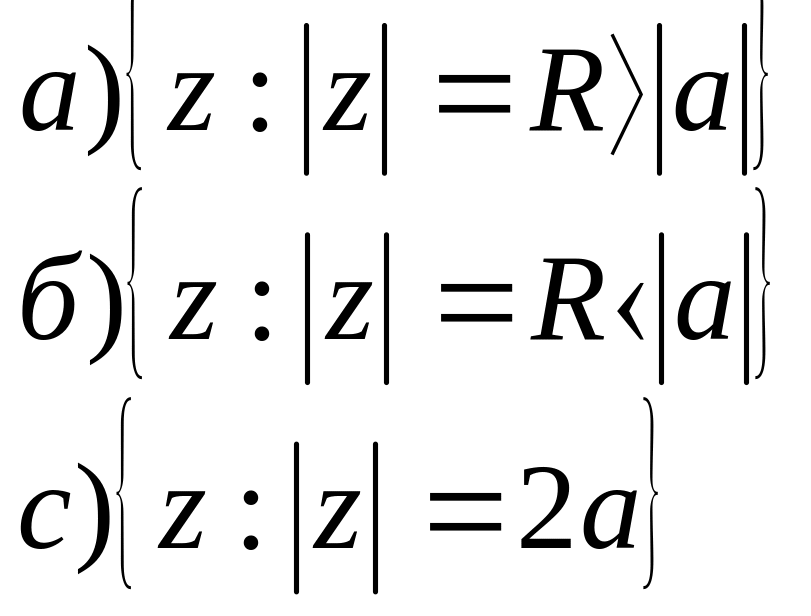
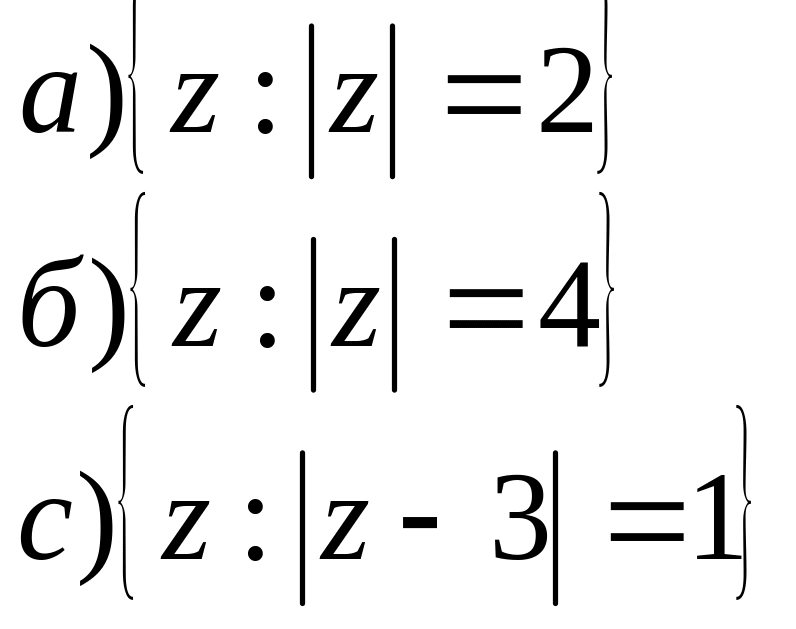
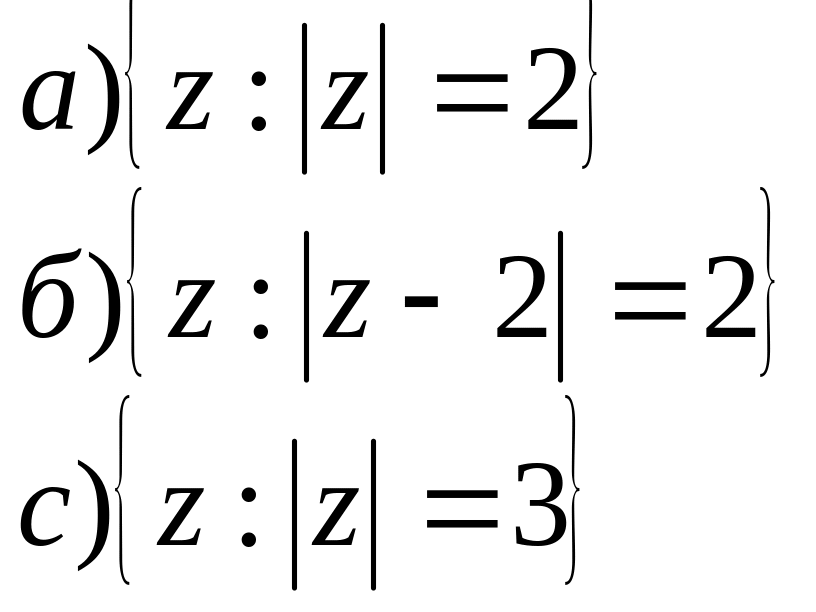
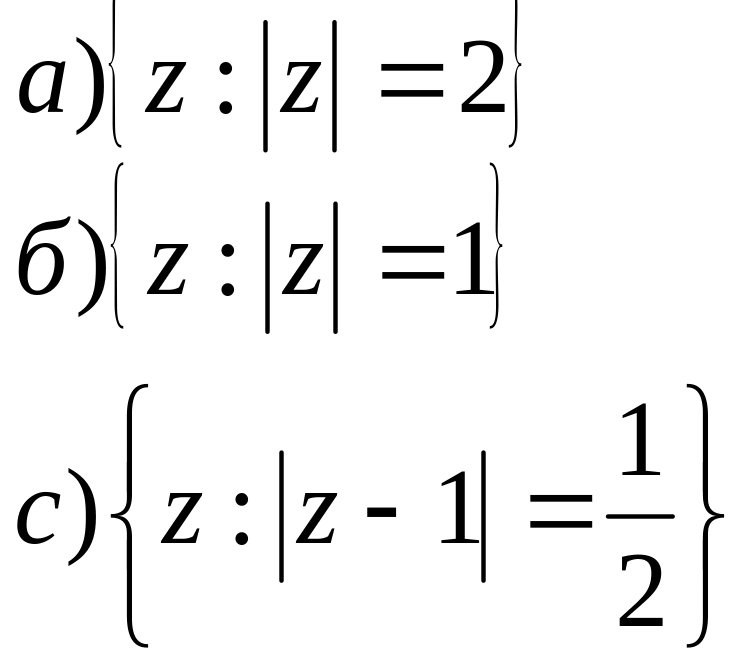
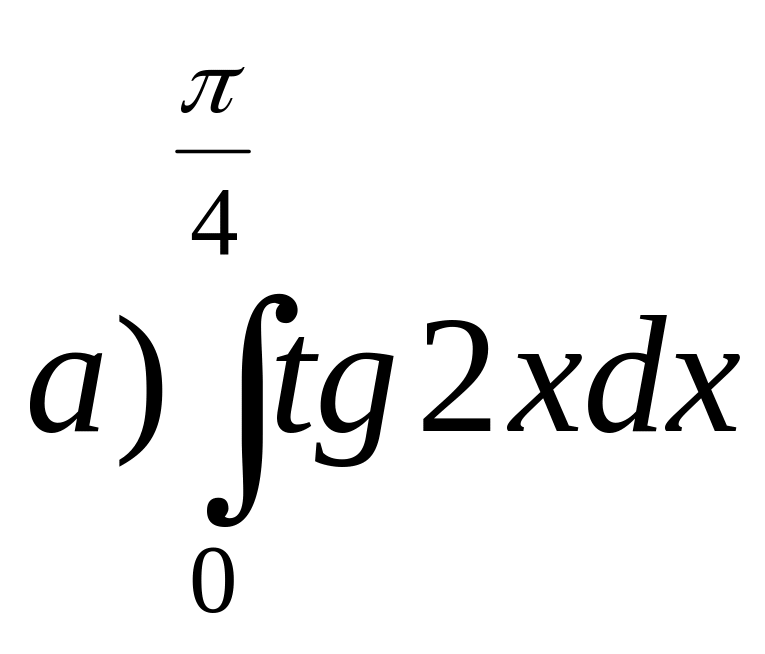