
- •Комплексні числа і дії над ними.
- •Побудова геометричних місць точок для заданих співвідношень.
- •Розв’язки:
- •Елементарні функції комплексної змінної.
- •Диференціювання функції комплексної змінної.
- •Інтегрування функції комплексної змінної.
- •Інтеграли типу Коші.
- •Степеневі ряди в комплексній області.
- •Обчислення визначених інтегралів функції комплексної змінної за допомогою лишків.
Степеневі ряди в комплексній області.
Степеневі ряди в комплексній області мають вигляд
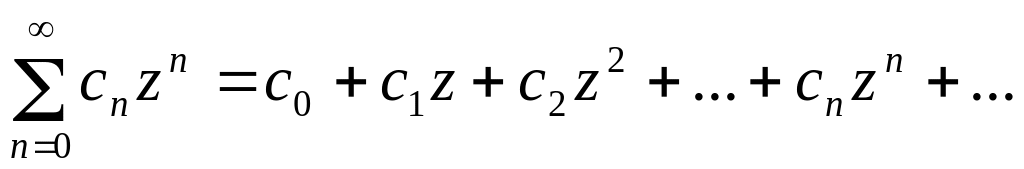
Теорема.
Якщо
степеневий ряд збігається в точці
![]() ,
то він збігається, причому абсолютно,
в усіх точках, що лежать в колі
,
то він збігається, причому абсолютно,
в усіх точках, що лежать в колі
![]()
![]() з центром в точці
,
а в будь-якому колі меншого радіусу ряд
збігається правильно. Радіус збіжності
степеневого ряду знаходиться за
формулами:
з центром в точці
,
а в будь-якому колі меншого радіусу ряд
збігається правильно. Радіус збіжності
степеневого ряду знаходиться за
формулами:
![]() ,
або
,
або
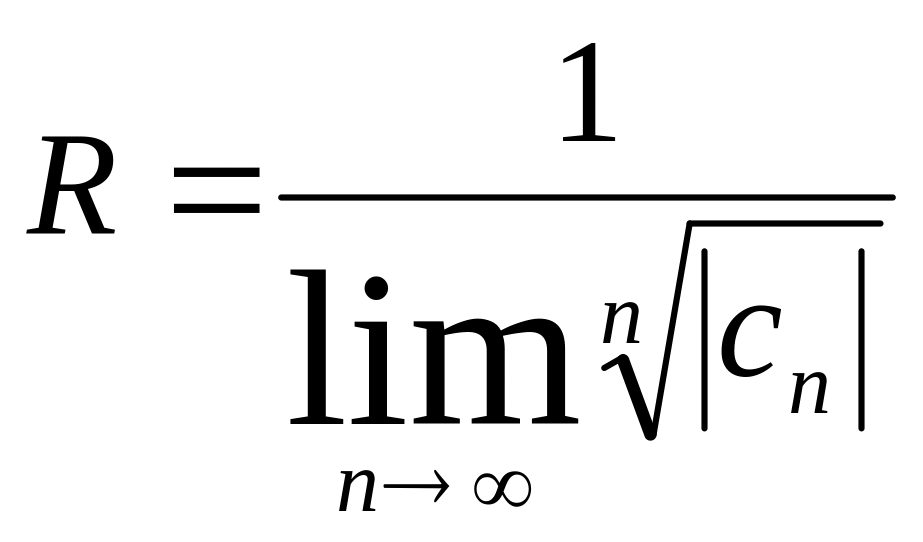
Ряд Тейлора. Якщо функція однозначна та аналітична в точці , то в околі цієї точки вона може бути розкладена в степеневий ряд Тейлора:
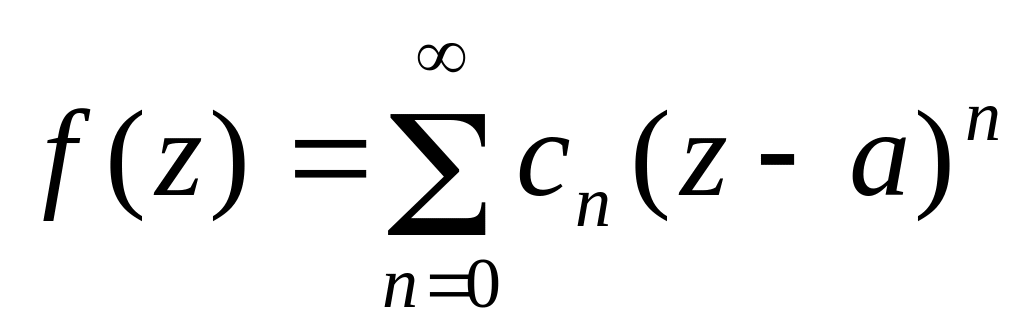 ,
де
,
де
![]() ,
,
![]()
Г
–
коло
![]()
![]() яке проходить через особливу точку
яке проходить через особливу точку
![]() ,
таку, що
,
таку, що
![]() .
Таким чином розвинення функції
комплексної змінної в ряд Тейлора має
такий самий вигляд, як і для функції
дійсної змінної:
.
Таким чином розвинення функції
комплексної змінної в ряд Тейлора має
такий самий вигляд, як і для функції
дійсної змінної:
![]()
Ряд
Лорана.
Якщо функція
однозначна та аналітична в кільці
![]() ,
то вона може бути розвинена в цьому
кільці в степеневий ряд Лорана:
,
то вона може бути розвинена в цьому
кільці в степеневий ряд Лорана:
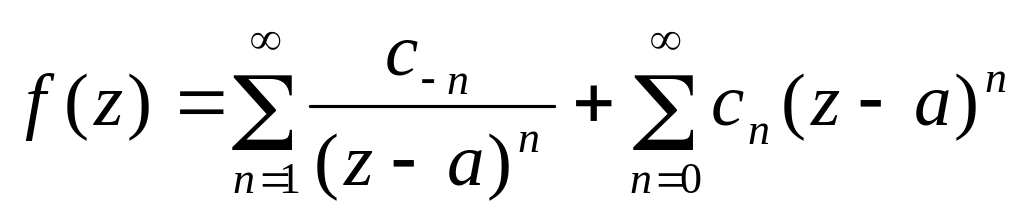 ,
де
,
де
![]() ;
;
![]() .
.
Г – коло довільного радіуса з центром в точці , що лежить по середині кільця.
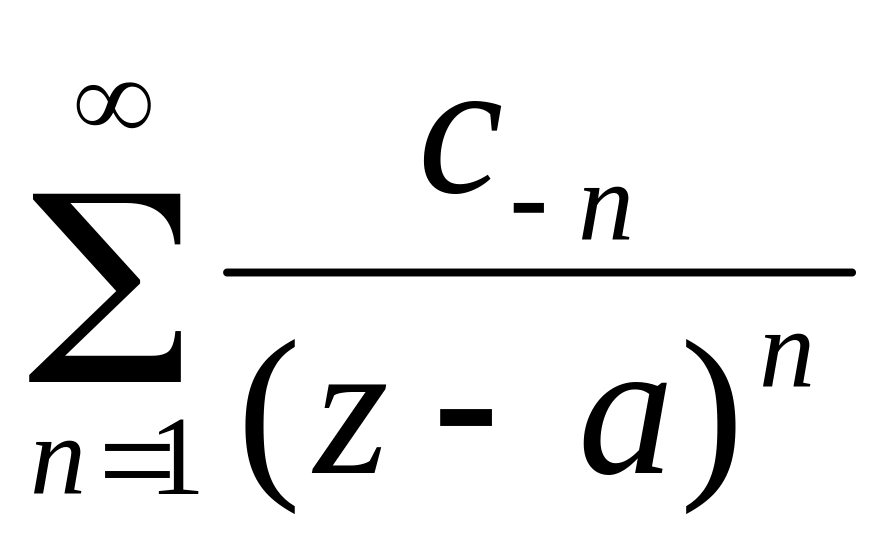 та
та
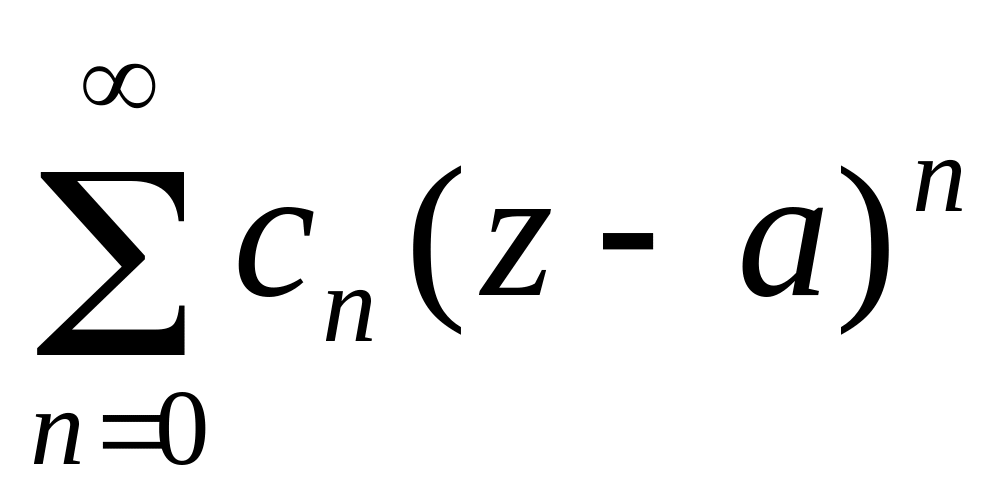 -
відповідно головна та правильна частина
ряду Лорана.
-
відповідно головна та правильна частина
ряду Лорана.
Особливі точки. Точка, в околі якої аналітична функція може бути розвинена в ряд Тейлора, називається звичайною. Будь-яка інша точка називається особливою точкою.
Полюса
– це ізольовані особливі точки, біля
яких функція
залишається однозначною і які є
звичайними точками для функції
![]() .
Для того, щоб точка
була
полюсом функції
,
необхідно і достатньо, щоб головна
частина лоранівського розвинення
в околі цієї точки містила лише скінченне
число членів.
.
Для того, щоб точка
була
полюсом функції
,
необхідно і достатньо, щоб головна
частина лоранівського розвинення
в околі цієї точки містила лише скінченне
число членів.
![]() ,
(
,
(![]() ).
).
Найбільший
із показників степенів
![]() ,
що міститься у знаменниках головної
частини ряду Лорана, співпадає з порядком
полюсу. Істотно
особливі
точки
–
це ізольовані особливі точки, в околі
яких функція
залишається
однозначною, але які є особливими і для
функції
.
,
що міститься у знаменниках головної
частини ряду Лорана, співпадає з порядком
полюсу. Істотно
особливі
точки
–
це ізольовані особливі точки, в околі
яких функція
залишається
однозначною, але які є особливими і для
функції
.
Точка тоді , і тільки тоді, є істотно особливою точкою для функції , коли головна части на її лоранівського розвинення містить нескінчене число членів. В цій точці не існує границі функції . Усувною особливою точкою функції називається така особлива точка, в якій функція має скінченну границю. Лоранівське розвинення в цій точці не містить головної частини. Критичні точки, або точки розгалуження – це особливі точки, біля яких функція не лишається однозначною.
Приклади особливих точок.
функція
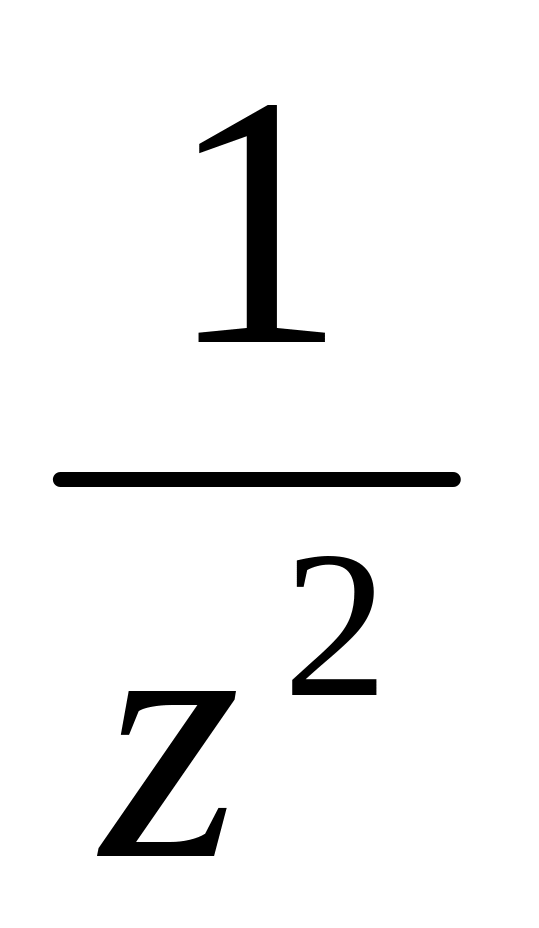 має полюс другого порядку
має полюс другого порядку
функція
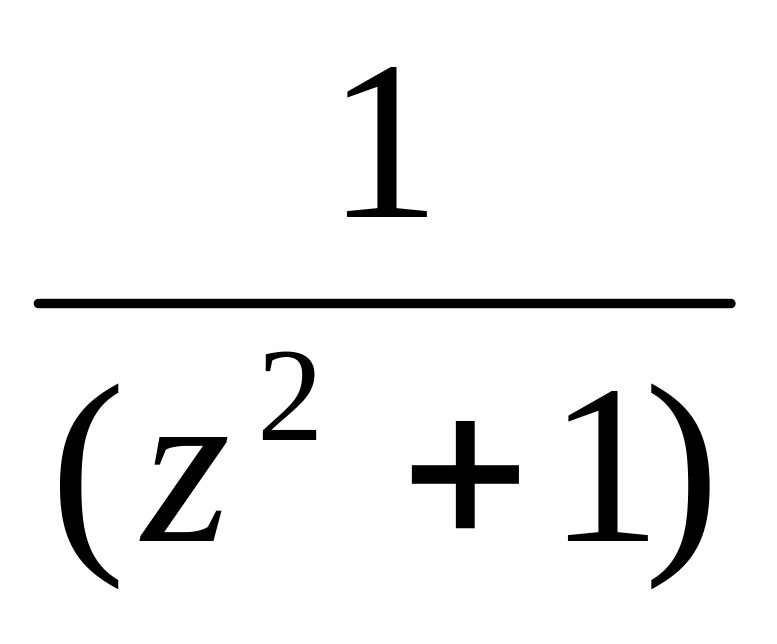 має прості полюси
має прості полюси
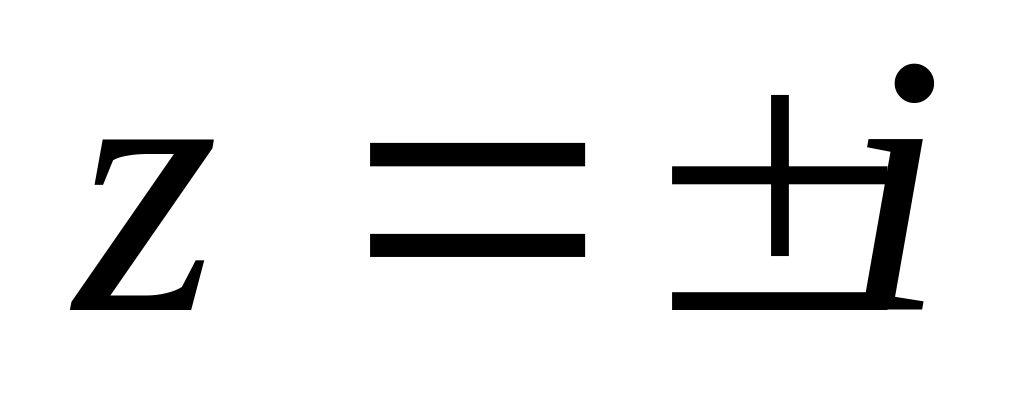
функція має істотно особливу точку
функція
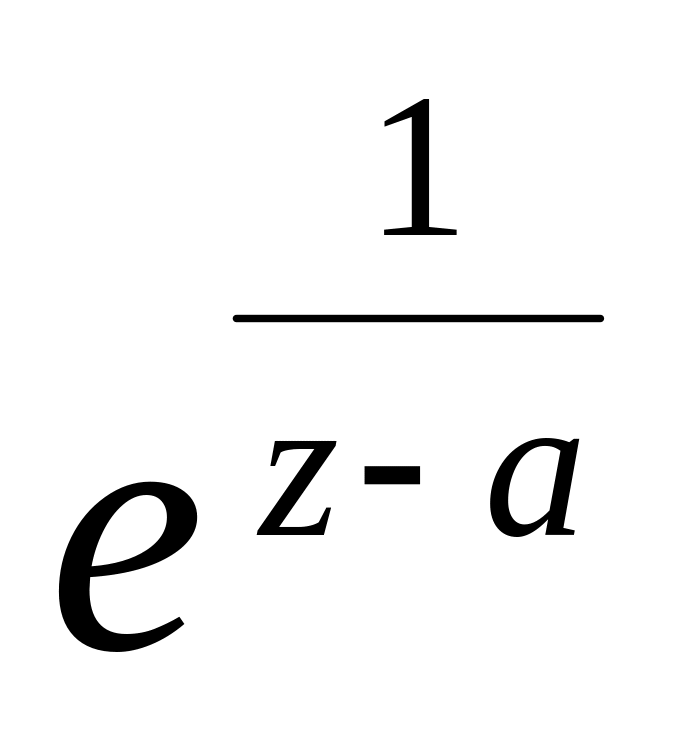 має істотно особливу точку
має істотно особливу точку
функція
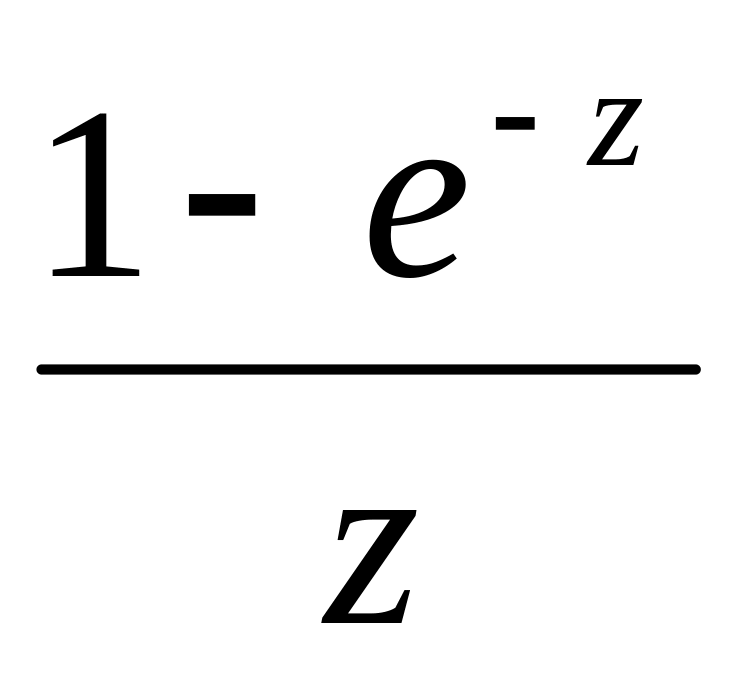 має усувну особливу точку
має усувну особливу точку
функція
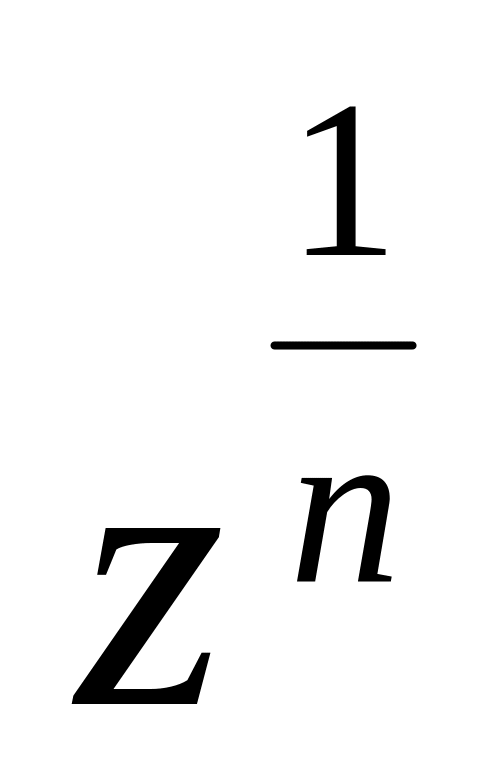 має точку розгалуження
має точку розгалуження
Приклади:
1.
Розкласти в ряд Лорана функцію
![]()
Розв’язок:
1) Біля полюса розклад в ряд Лорана має вигляд
![]()
2) Біля
полюса
![]() маємо
маємо
![]()
2.
Розкласти в ряд Лорана функцію
![]() в кільці
в кільці
Розв’язок:
Запишемо
функцію
як суму двох простих дробів
![]() .
.
Оскільки
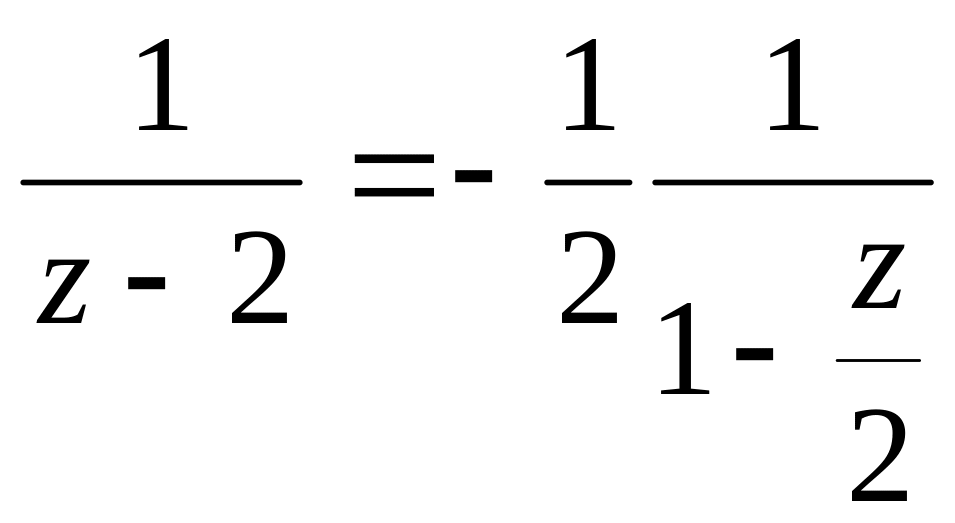 - є сумою геометричної прогресії, модуль
знаменника якої
- є сумою геометричної прогресії, модуль
знаменника якої
![]()
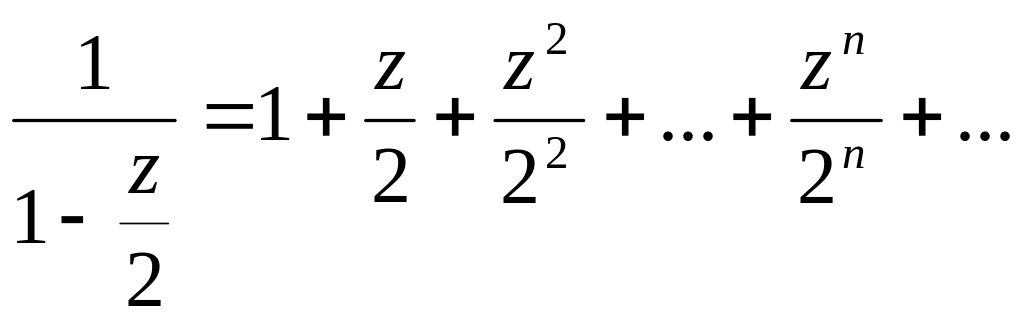 ,
то
,
то
![]()
Ряд в правій частині збіжний, тому що
Другий дріб перепишемо у вигляді
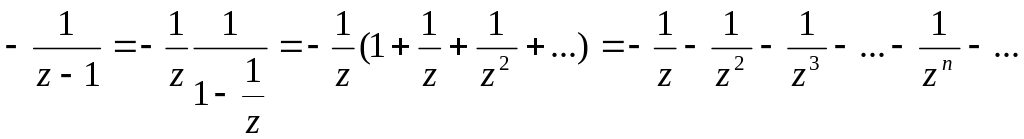
Ряд в
правій частині збіжний в кільці
,
тому що
![]() і, отже
і, отже
![]() .
.
З цього
випливає, що ![]()
3.
Розкласти в ряд Лорана в околі точки
функцію
![]()
Розв’язок:
Маємо:
![]()
Враховуючи, що
![]()
![]()
Знаходимо
![]()
Лекція 14
