Інтегрування функції комплексної змінної.
Обчислення
інтеграла від функції комплексної
змінної зводиться до обчислення
звичайних криволінійних інтегралів.
Якщо
,
,
то
.
.
Приклади.
1.
Обчислити
а)
с-відрізок
б)
с-дуга параболи
,
;
в)
с-відрізки
V
,
(
).
Розв’язки:
Якщо
,
,
то
,
де
,
.
За
формулою
маємо:
.
а
)
Контур С-відрізок
,
(Рис. 10)
тому
б
)
Контур С-дуга параболи
;
(Рис. 11)
маємо
в) Контур
С=С1+С2
(Рис. 11/)
V
маємо
;
,
;
;
,
;
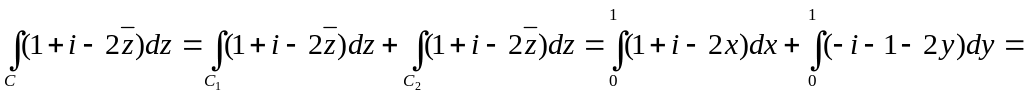
1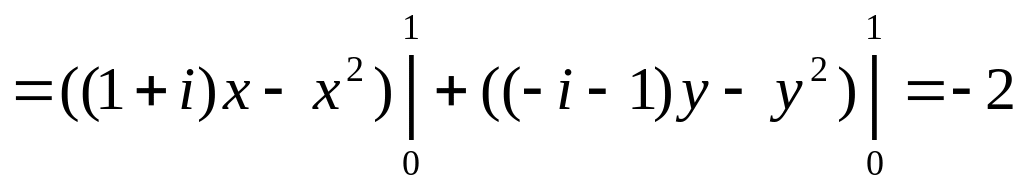
2.
Обчислити
,
(Рис.
12)
Рішення:
Розглянемо
в показниковій
формі
,
,
тоді
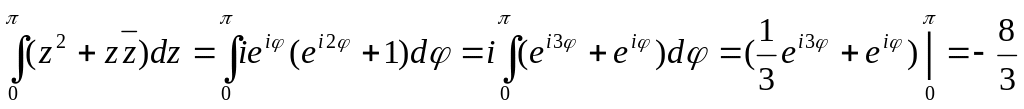
Лекція 12
Теорема Коші. Якщо функція аналітична в однозв’язній області, обмеженій замкненим контуром Г , а також в точках цього контура, то
У випадку багатов’язної області
;
У випадку двозв’язної області (Рис. 13)
Г
Рис. 13
Інтегральна формула Коші.
Розглянемо
інтеграл
,
де Г-замкнений контур, обмежуючий
область D.
Якщо точка
,
то
аналітична функція всередині D
і на Г. Тоді на підставі теореми Коші:
Нехай
точка
і обходиться контуром Г в додатному
напрямі 1 раз. Вибравши коло
радіусом R
з
центром в точці а , тобто
,
,
знайдемо
.
Отже,
.
Теорема. Якщо функція аналітична в області D, обмеженій замкненим контуром Г, і на самому контурі Г, то
, (1)
де
,
,
і контур Г обходиться в додатному
напрямі. Рівність (1) називається 1-ою
інтегральною формулою Коші, а інтеграл
-
інтегралом Коші.
Інтеграли типу Коші.
Теорема. Якщо функція аналітична в області D і на її границі Г, то для довільного натурального n можна записати формулу
, (2)
де , .
Рівність (2) називається 2-ою інтегральною формулою Коші, а інтеграл
-
інтегралом типу Коші.
Приклад.
О
Г
D
бчислити:
R=
0
1
а)
Г:
б)
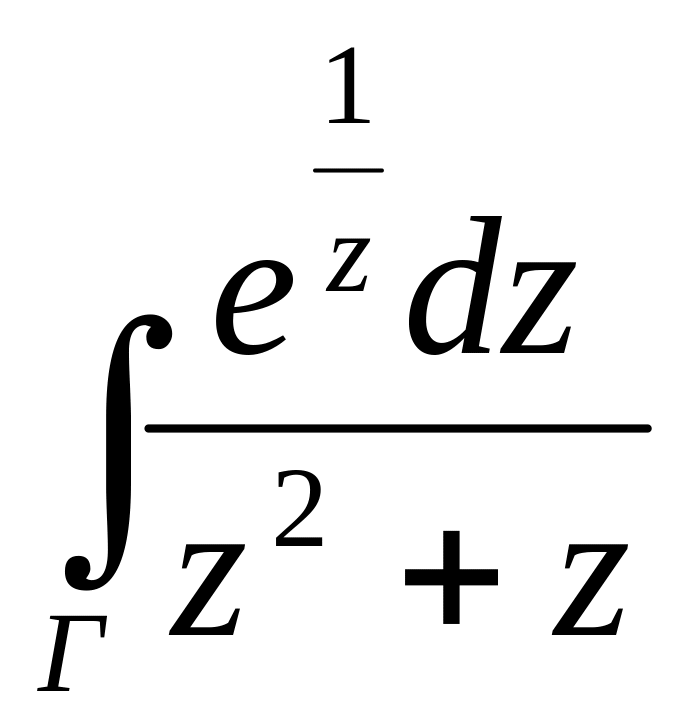Г:
Рис. 14
Розв’язки:
а)
,
- особливі точки (полюса) не належать
області D
(Рис. 14)
Тому функція всередині області D і на контурі Г аналітична. Отже,
Г:
б)
,
,
- особливі точки:
,
.
Оточимо точки
(Рис.
15) колами
і
малих радіусів – тоді
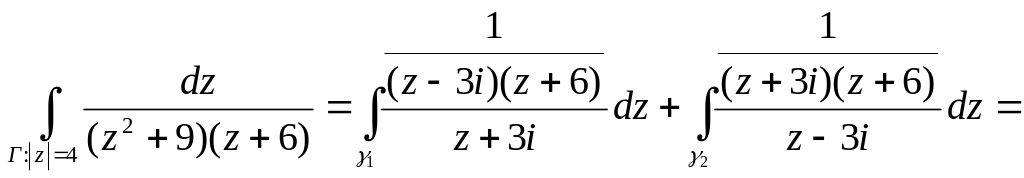
-4
R=4
4
Г
0
-3i
3i
4
.
Обчислити
а)
б)
Рис. 15
Розв’язки:
а) - особлива точка (полюс кратності 3). Ця точка належить області D (Рис. 16).
Застосувавши формулу (2), маємо
б) Особливі точки:
-
полюс кратності
(Рис.
17).
Застосувавши формулу (2), маємо
9
Г
R=6
-3
2
0
D
3
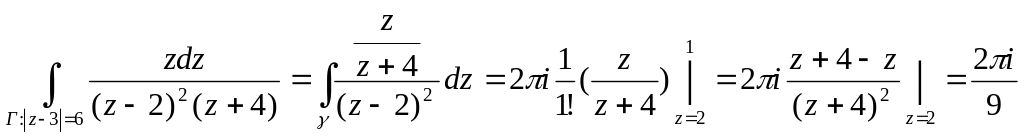
Рис. 16
-4
Рис. 17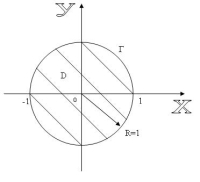
Лекція 13