24

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Тверской государственный технический университет» (гоувпо ТвГту)

Математическая статистика

В машиностроении

Сборник задач

Тверь 2012

Сборник задач по дисциплине «Математическая статистика в машиностроении»: Г.Б. Бурдо, Г.И. Рогозин, Ф.Х.Арсланов. Тверь: ТГТУ, 2012 Г.

Представлены задачи по основным разделам дисциплины «Математическая статистика в машиностроении»: применение методов математической статистики для анализа точности механической обработки, настройки станков, контроля качества продукции и т. д.

Каждый тип задач сопровожден подробными методическими ука­заниями и решением. Сборник задач предназначен для бакалавров, изучающих дисциплины ”Математическая статистика в технологии машиностроения” и «Теория вероятностей в технологии машиностроения» направлений 151900 и 227000 программы для высших учебных заведений.

1. Условия задач Задача №1

Непрерывная случайная величина имеет следующее распределение:

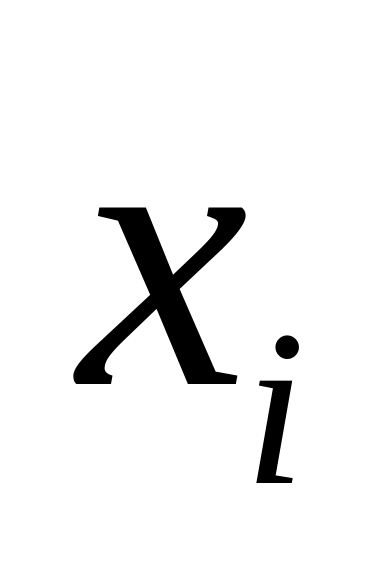
Интервалы Значений х	Середина Интервала	Частота fi
2-6 6-10 10-14 14-15	4 8 12 16	1 4 4 1

Определить среднее арифметическое и среднее квадратическое отклонение

Задача № 2

По выборке объема п = 15 найдено X = 20,4 и s = 0,8. Определить истинное значение генеральной средней Х₀.

Задача №3

Установить, какой объем n выборки необходимо взять, чтобы определить по этой выборке генеральную среднюю с точностью = ±2 и

вероятностью = 0,95.

Задача №4

Определить точность приближенного равенства ₀ s с вероятностью

= 0,96, если n = 15 и s = 0,12.

Задача № 5

Определить п, при котором s будет отличаться от ₀ на ±0,2 с вероятностью = 0,96.

Задача № 6

Определить точность приближенного равенства ₀ s с вероятностью = 0,95, если n = 50, s = 0,1.

Задача№7

Определить вероятность приближенного равенства ₀ s, если n =50,

= 0,1.

Задача №8

Из текущей продукции автомата, обрабатывающего ролики D = 20_₀₎₂ мм, была взята выборка объемом п = 100 шт. Ролики были измерены по диаметру микрометром с ценой деления 0,01 мм. Ниже приведены отклонения от номинального размера диаметра роликов в мм:

Определить статистические характеристики распределения, т. е. и s.

Задача№9

По данным примера 19 сопоставить эмпирическую кривую с теоретической кривой по закону нормального распределения и вычислить координаты характерных точек для построения теоретической кривой распределения.

Задача №10

Сопоставить эмпирическое распределение по данным задачи 8 с законом нормального распределения при помощи таблицы значений Ф .

Задача №11

По данным примеров 20 и 21 вычислить критерий и проверить гипотезу нормальности.

Задача№12

С автомата, обрабатывающего втулки D = 20мм, было взято в разное время две выборки по 5 шт. каждая. Результаты измерения диаметров втулок приведены в табл. ниже.

Распределение диаметров втулок предполагается нормальным.

Используя критерий t Стюдента показать, что настройка станка в момент взятия пробы №1 и №2 не изменилась.

Задача №13

При одних и тех же условиях было обработано по 25 шт. втулок разверткой d = 6 мм и разверткой d = 10 мм. Результаты измерений двух партий втулок показали, что средняя величина разбивки отверстий (разность между диаметром отверстия и диаметром развертки) составляет для d = 6 мм Х₁=10,4 мкм, для d = 10 мм

Х₂ =9,8 мкм. Дисперсии величин разбивок соответственно равны: = 3,8 мкм² и = 4,76 мкм².

Необходимо установить, влияет ли диаметр развертки на величину разбивки отверстий, если предварительными опытами установлено, что рассеивание величин разбивки подчиняется нормальному закону распределения.

Задача №14

С двух автоматов, обрабатывающих одинаковые детали, взято две выборки = п₂ = 10. При этом оказалось, что = 400 мкм² и

= 325 мкм². Ранее было установлено, что рассеивание размеров деталей, обработанных на автоматах, следует нормальному закону распределения.

Можно ли считать, что оба станка обеспечивают одинаковую точность обработки?

Задача №15

С четырех автоматов, настроенных на обработку одних и тех же деталей, взято по одной текущей выборке объема п₁ = п₂ = п₃ = n₄ = 10. Дисперсии выборок имеют следующие значения: = 100 мкм², = 300 мкм², = 200 мкм², = 400 мкм². Требуется установить, одинакова ли точность автоматов, т. е. одинаково ли рассеивание случайных погрешностей обработки на этих автоматах, если предварительными исследованиями установлено, что это рассеивание подчиняется закону нормального распределения.

Задача №16

С двух станков, настроенных на обработку одной и той же детали, взяты текущие выборки объема n = m= 15. Результаты измерения деталей выборок приведены в табл., где через х обозначены отклонения измеряемого размера от номинала в мкм для выборки со станка № 1, а через у — отклонения в мкм измеряемого размера для выборки со станка № 2.

Требуется определить, можно ли считать точность обработки двух станков одинаковой. Другими словами, нужно проверить нулевую гипотезу о том, что распределения погрешностей обработки двух станков описываются одинаковыми функциями распределения.

Таблица

Результаты измерения деталей выборок

Задача № 17

Определить вероятность получения годовой продукции, если точность метода обработки  = 0,12 мм, а допуск 0,08 мм. Границы поля допуска относительно центра группирования расположены симметрично.