8. Найти производную функции в точке по направлению s
,
,
Если функция
дифференцируема, то её производная
по любому направлению S
существует и равна
,
где
- направляющие косинусы луча S.
Преобразуем функцию
к виду удобному для дифференцирования
.
.
Найдем направляющие косинусы луча S.
,
где
.
,
,
.
Ответ:
9. Найти поток
векторного поля
через внешнюю сторону замкнутой
поверхности
.
Если векторное
поле
непрерывно дифференцируемо внутри
замкнутой поверхности
,
то можно использовать формулу Гаусса
– Остроградского для вычисления потока
в направлении внешней нормали:
,
где V – тело, ограниченное замкнутой поверхностью S.
Найдем дивергенцию поля, которая вычисляется по формуле:
.
В нашем случае
имеем:
;
;
.
,
,
.
Следовательно,
.
Тело V,
границей которого является поверхность
S,
представляет собой треугольную пирамиду,
ограниченную координатными плоскостями
и плоскостью
(
).
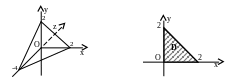
Ответ:
.
10. Найти общее решение дифференциального уравнения
а)
,
б)
,
в)
а)
,
,
,
.
Ответ: - общий интеграл дифференциального уравнения.
б) ,
Пусть
.
Тогда
.
Получили уравнение относительно функции
u:
.
,
,
.
Ответ:
- общий интеграл дифференциального
уравнения.
в)
Пусть
.
Тогда
.
Получим уравнение относительно функции
u:
.
,
,
.
Ответ:
- общий интеграл дифференциального
уравнения.
11. Решить задачу Коши для дифференциального уравнения
,
.
Пусть
.
Тогда
.
Получим уравнение
,
,
,
- общее решение
дифференциального уравнения.
Найдем С, удовлетворяющее начальному условию .
Ответ:
- частное решение дифференциального
уравнения, удовлетворяющее начальному
условию
.
12. а) Найти общее решение однородного дифференциального уравнения высшего порядка
.
Характеристическое уравнение
.
.
- действительный
корень кратности три,
- пара комплексных
корней.
- частные решения
дифференциального уравнения,
соответствующие корням характеристического
уравнения.
- общее решение
однородного дифференциального уравнения
пятого порядка.
б) Найти общее решение неоднородного дифференциального уравнения высшего порядка
.
- неоднородное дифференциальное уравнение шестого порядка.
- соответствующее
однородное уравнение.
- характеристическое
уравнение.
.
- действительный корень кратности четыре,
- пара комплексных
корней.
- частные решения дифференциального уравнения, соответствующие корням характеристического уравнения.
- общее решение
однородного дифференциального уравнения
шестого порядка.
- правая часть
неоднородного уравнения.
- многочлен третьей
степени, число
является корнем характеристического
уравнения кратности четыре, поэтому
частное решение имеет вид
.
Находим неопределенные
коэффициенты.
.
Подставляем производные в исходное
уравнение
.
.
Отсюда
.
.
Частное решение,
соответствующее правой части
имеет вид
.
.
Число
не является корнем характеристического
уравнения, поэтому частное решение
имеет вид
.
Находим неопределенные
коэффициенты.
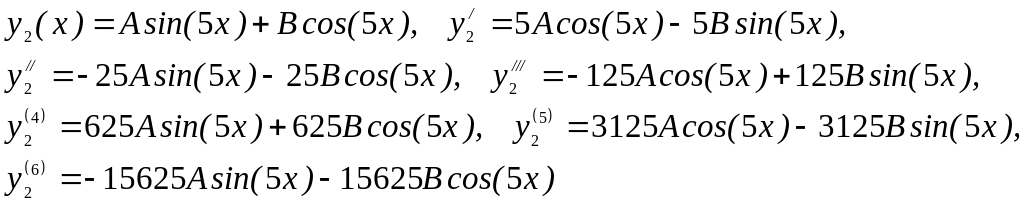
Подставляем
производные в исходное уравнение
.
.
.
Частное решение,
соответствующее правой части
имеет вид
.
.
Число
является корнем характеристического
уравнения кратности один, поэтому
частное решение имеет вид
.
Находим неопределенные
коэффициенты.
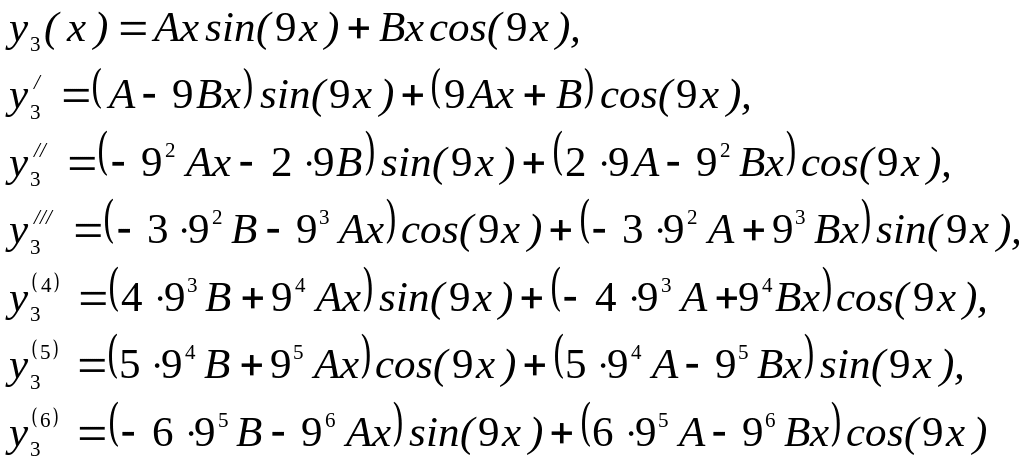
Подставляем
производные в исходное уравнение
.
.
Частное решение,
соответствующее правой части
имеет вид
.
Частное решение,
соответствующее правой части
,
имеет вид
,
то есть
.
Общее решение
неоднородного уравнения
имеет вид
.
.
