
- •Введение
- •1. Кинематика Краткие теоретические сведения
- •Кинематика поступательного движения
- •Уравнения кинематики для различных видов поступательного движения
- •Кинематика вращательного движения твёрдого тела
- •Уравнения кинематики для различных видов вращательного движения твёрдого тела
- •Примеры решения задач на кинематику
- •2. Динамика Краткие теоретические сведения
- •Динамика поступательного движения
- •Основные законы динамики поступательного движения
- •Динамика вращательного движения
- •Основные законы динамики вращательного движения
- •Примеры решения задач на динамику
- •3. Колебания Краткие теоретические сведения
- •Сложение одинаково направленных колебаний.
- •Сложение взаимно перпендикулярных колебаний.
- •Примеры решения задач на колебательное движение
- •4.1 Молекулярная физика и термодинамика Краткие теоретические сведения
- •Примеры решения задач на колебательное движение
Сложение одинаково направленных колебаний.
Если тело одновременно участвует в колебаниях:
|
|
|
|
то его результирующее колебательное движение будет описываться уравнением:
|
|
где
![]() – амплитуда результирующего колебания,
– амплитуда результирующего колебания,
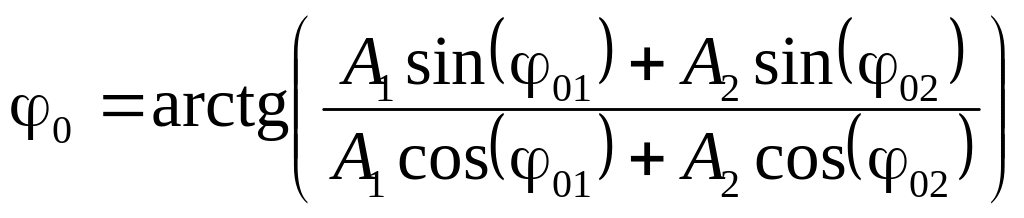 -
начальная фаза результирующего колебания.
-
начальная фаза результирующего колебания.
Сложение взаимно перпендикулярных колебаний.
Сложение двух
колебаний в случае, когда они перпендикулярны
друг другу, не всегда приводит к
колебательному движению. Чаще всего
задачи на сложение перпендикулярно
направленных колебаний сводятся к
отысканию траектории движения тела.
Для нахождения траектории нужно получить
зависимость одной координаты тела от
другой (например
![]() )
и по виду получившегося уравнения
сделать вывод о форме траектории.
)
и по виду получившегося уравнения
сделать вывод о форме траектории.
Примеры решения задач на колебательное движение
Задача 3.1: Написать уравнение гармонического колебательного движения с амплитудой 10 см, периодом 2 с и начальной фазой /3. Найти смещение колеблющейся точки от положения равновесия, её скорость и ускорение при t1 = 0 и при t2 = 2,5 с.
Дано: A = 10 см = 0,1 м T = 2 с
0
=
t1 = 0 t2 = 2,5 с |
Р
(1)
где x
– смещение точки в момент времени t;
С учётом условия задачи, получаем:
(2) |
||||
x x (t1), x (t2) – ? x (t1), x (t2) – ? ax (t1), ax (t2) – ? |
2. Смещение точки в моменты времени t1 и t2 можно найти, подставив в уравнение (2) соответствующие значения времени:
|
|
|
|
3. Чтобы найти скорость колеблющейся точки в разные моменты времени, необходимо получить уравнение для скорости точки. Это можно сделать, воспользовавшись определением скорости:
|
|
Таким образом, для нахождения уравнения скорости достаточно определить производную по времени от смещения точки (2):
|
(3) |
Подставляя t1 и t2, получим значения скорости точки в эти моменты времени:
|
|
|
|
4. Чтобы найти ускорение колеблющейся точки в разные моменты времени, необходимо получить уравнение для ускорения точки. Это можно сделать, воспользовавшись определением ускорения:
|
|
Таким образом, для нахождения уравнения ускорения достаточно определить производную по времени от скорости точки (3):
|
(4) |
Подставляя t1 и t2, получим значения ускорения точки в эти моменты времени:
|
|
|
|
Ответ: x(t1) = 0,05 м; x(t2) = -0,09 м; x(t1) = -0,14 м/с; x(t2) = -0,16 м/с;
ax(t1) = -0,49 м/с2; ax(t2) = 0,43 м/с2.
Задача 3.2: Амплитуда гармонических колебаний материальной точки 3 см, полная энергия колебаний W = 0,3 мкДж. При каком смещении х от положения равновесия на колеблющуюся точку действует сила F = 22,5 мкН.
Дано: A = 3 см = 310-2 м W = 0,3 мкДж F = 22,5 мкН
|
Р 1. Силу, действующую на колеблющуюся точку можно найти с помощью II закона Ньютона:
|
||
x – ? |
Пусть уравнение гармонических колебаний точки имеет вид:
, |
(1) |
тогда модуль ускорения точки:
|
|
3. Теперь можно записать уравнение для модуля силы, действующей на точку:
|
(3) |
4. Полная энергия колебаний точки определяется уравнением:
|
(4) |
5. Поделим уравнение (3) на (4):
|
|
откуда:
|
|
Ответ: x = 3,4 см.
Задача 3.3: Написать уравнение результирующего колебания, получающегося в результате сложения двух одинаково направленных колебаний с одинаковыми частотами 1 = 2 = 5 Гц. Амплитуды колебаний равны A1 = 10 см, А2 = 15 см, начальные фазы – 01 = 0, 02 = /6.
Д ано: 1 = 2 = 5 Гц A1 = 10 см = 0,1 м А2 = 15 см = 0,15 м 01 = 0 02 = /6 |
Решение: 1. Так как частоты колебаний равны, то и циклические частоты тоже будут равны:
|
||
x (t) –? |
|
2. Запишем уравнения колебательного движения для обоих колебаний в виде:
|
|
3. Амплитуда результирующего колебания находится по формуле:
|
|
4. Начальная фаза результирующего колебания:
|
|
5. Произведя расчёты, теперь мы можем записать уравнение результирующего колебания:
|
|
Ответ:
![]() ,
м
,
м
Задача 3.4: Найти траекторию движения колеблющейся точки, получающуюся в результате сложения двух перпендикулярно направленных колебаний с одинаковыми частотами 1 = 2 = 5 Гц и начальными фазами 01 =02= 0. Амплитуды колебаний равны A1 = 10 см, А2 = 15 см.
Д 1 = 2 = 5 Гц A1 = 10 см = 0,1 м А2 = 15 см = 0,15 м 01 = 02 = 0 |
Решение: 1. Так как частоты колебаний равны, то и циклические частоты тоже будут равны:
.
|
|||
y |
||||
|
|
|||
|
|
3. Для получения уравнения траектории поделим одно уравнение на другое:
|
|
откуда
|
|
Полученное уравнение
имеет вид
![]() .
Это уравнение прямой. Значит траектория
тела имеет вид прямой линии.
.
Это уравнение прямой. Значит траектория
тела имеет вид прямой линии.
Ответ:
![]() ,
м, траектория – прямая.
,
м, траектория – прямая.

 ешение:
ешение: (t)
– ?
(t)
– ? ешение:
ешение: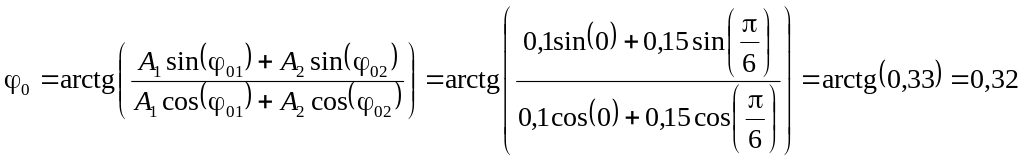 .
. ано:
ано: (x)
–?
(x)
–?