Үзіліссіз функциялар
§1. Функциялардың үзіліссіздігі мен үзілуі
1. Үзіліссіздіктің әр түрлі анықтамалары. Үзіліссіздікті дәл анықтаудың алдында, сол ұғымға келтіретін бір көрнекі мысалды қарастырайық. 31-суретте L және L қисықтары сызылған. «Осы екі қисықтың қайсысын «үзіліссіз қисық» деп атауға болар еді?»- деген сұраққа, әрине, мынадай жауап беруге болады: L – сөзсіз «үзіліссіз» болады да, L - жалпы алғанда «үзіліссіз» болып көрінгенмен, хо нүктесінде «үзіледі».
L және L қисықтары сәйкес f және g функцияларының графиктері болсын. Әрине, графигі «үзіліссіз қисық» болатын функцияны үзіліссіз деп, ал оған қарама-қарсы жағдайда – үзілісті функция деп атаған жөн. Бұны функцияның үзіліссіздігі мен үзіліссіздігінің алдын ала берілген уақытша анықтамасы ретінде қабылдап, сол ұғымды құрайтын қасиеттерді дәл анықтауға тырысайық.
Ең алдымен f(х) функциясының анықтау керек болатын үзіліссіздік қасиеті оның графигі L қисығының әрбір нүктесіне тән қасиеттерімен тығыз байланысты екенін атап өтейік. Сондықтан, үзіліссіздікті барлық х-тер үшін анықтау мәселесі әрбір жеке х үшін анықтау мәселесіне тіреледі.
Сонымен, х=хо болсын. Осы хо нүктесіне байланысты f(х) функциясының қасиеттері қандай болу керек?
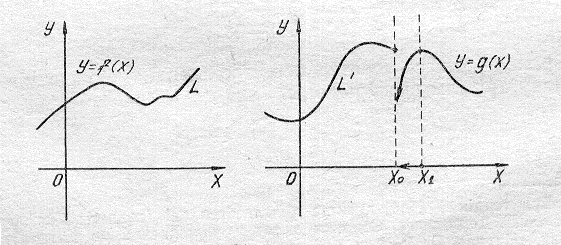
Б і р і н ш і д е н, f функциясының х0 нүктесінде анықталғандығы қажет. Бұл өте маңызды, өйткені f(хо) анықталған болмаса, онда l қисығында бір нүкте жетіспес еді.
Е к і н ш і д е н, f функциясы х0 нүктесінің «қасындағы» барлық нүктелерде, яғни белгілі бір оң саны үшін хо, хо , хо, хо хо, хо жиындарының бірінде анықталуы қажет.
Ү ш і н ш і д е н, х нүктесі хо-ге оң жағынан да, сол жағынан да ақырсыз жақындағанда, f(х) f(хо)-ге ақырсыз жақындау керек (31-суреттен мынаны көруге болады: х нүктесі хо-ге оң жағынан ақырсыз жақындағанда у=g(х) функциясы үшін бұл қасиет орындалмайды).
Міне, енді осы үш қасиетке негізделген үзіліссіздіктің дәл математикалық анықтамасын бере аламыз.
f функциясы I аралығында анықталған болсын. а, b, (а, b), а, b), (а, b, (-, b), (а, +), (-, b, а, +), (-,+), а, b-нақты сандар (аb). Егер хо нүктесі үшін х хо-ге ұмтылғанда оған сәйкес f(х) f(хо)-ге ұмтылса, онда f функциясын хо нүктесінде үзіліссіз дейді.
Сонымен, үзіліссіздік шек ұғымы арқылы анықталады. Әрине, бұл анықтамада біз жоғарыда бөліп алған үш қасиет сақталған:
б і р і н ш і д е н, хо, яғни f(хо) анықталған,
е к і н ш і д е н, f функциясы аралығында анықталған, демек, хо болғанда (хо-, хо+) , хо, хо+) немесе (хо-, хо кірістірулерінің кемінде бірін қанағаттандыратын оң саны табылады,
ү
ш і н ш і д е н, соңғы қасиеттің дәл
мағынасы шек ұғымы арқылы берілген:
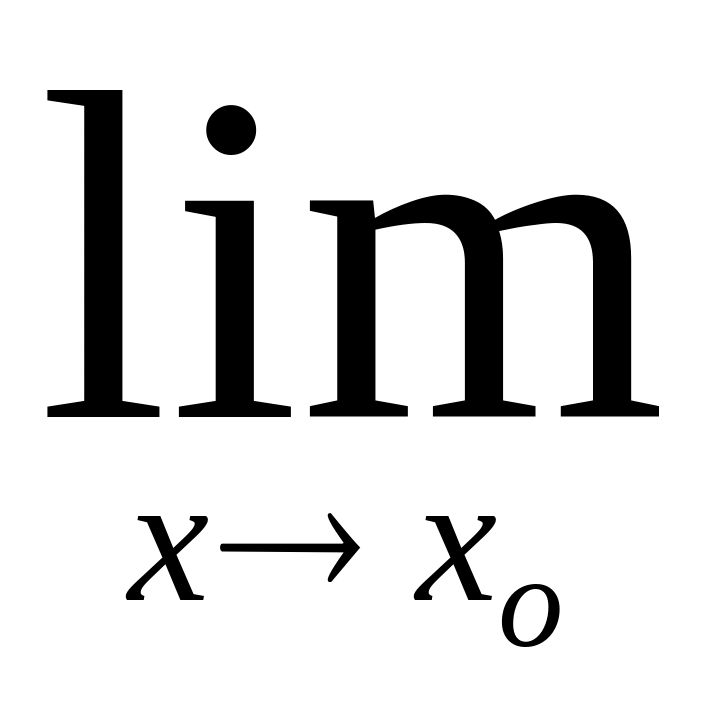f(х)
=
f(хо).
f функциясының хо нүктесінде үзіліссіз болуының анықтамасы шекті белгілеу үшін қолданылатын символдар арқылы былай жазылады:
1.
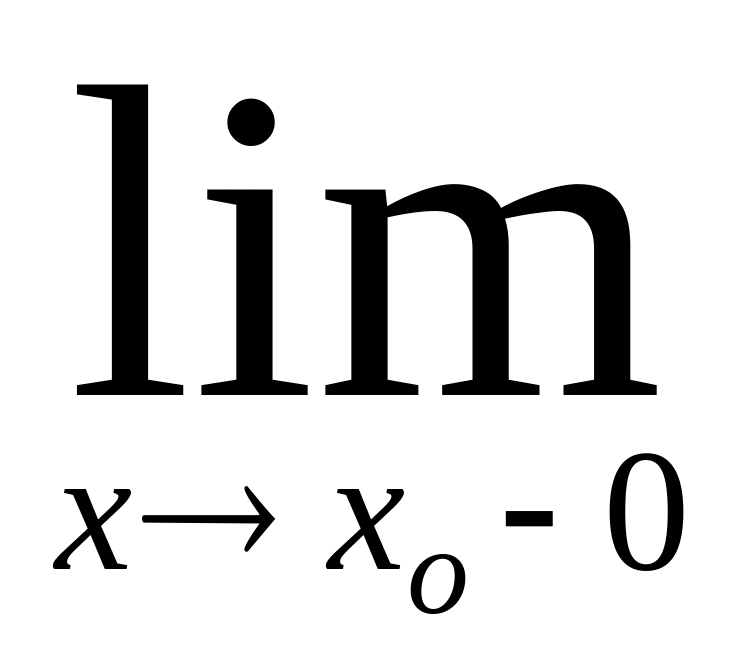f
(х) =
f
(хо)
=
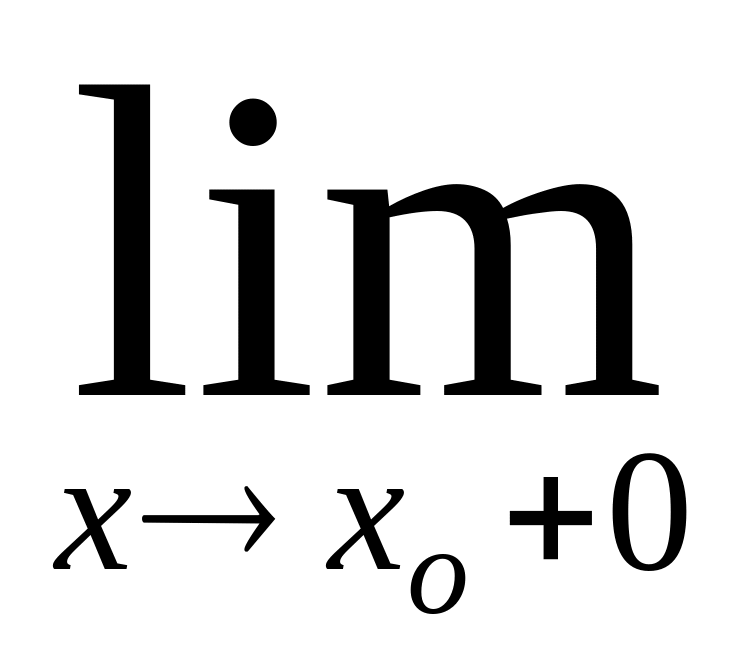f
(х).
2. f
(хо-0)
= f
(хо)
=
f(хо+0).
3. f(х) = f(хо). 4. f(х) - f(хо) =0.
5.
f(хо+h)
- f(хо)
=0.
6.
f(хо+х)
- f(хо)
=0.
7. у = 0. 8. f(х) f(хо) (х хо).
9. f(хо+h) - f (хо) 0 (h 0). 10. f (хо+х) - f (хо) 0 (х 0).
11. у 0 (х 0). 12. (х хо) (f (х) f (хо)).
13. (h 0) (f (хо+h) f (хо)). 14. (х 0) (f(хо+х)f(хо)).
15. (х 0) (у 0).
Бұнда х =х - хо=h, у=f(х)-f(хо) белгілері қолданылған (х пен у – тұтас символдар, сәйкес, , «дельта-икс» және «дельта-игрек» деп оқылады). х-хо=h=х сандары функцияның аргуметінің немесе тәуелсіз айнымалының хо нүктесіндегі өсімшесі деп, ал оған сәйкес
у= f(х) - f(хо) = f(хо+h) - f(хо) = f(хо+х) - f(хо)
саны функцияның немесе тәуелді айнымалының өсімшесі деп аталады.
перевод с каз.яз.на рус.яз.: К.Нуртазина