4) Проверка информации на выпадающие точки.

а) Грубую проверку информации на выпадающие точки проводят по «правилу трех сигм»: если крайние точки информации не выходят за пределы , то все точки информации считают дей­ствительными.

Так, в данном примере границы достоверности информации бу­дут равны:

• нижняя: t^н = 4150 - 3 ∙ 1150 мото-ч. = 700 мото-ч.;

• верхняя: t^в = 4150 + 3 ∙ 1150 мото-ч. = 7600 мото-ч.

Наименьший доремонтный ресурс двигателя 1500 мото-ч. Следовательно, эта точка информации действительна и должна быть учтена при дальнейших расчетах. Наибольший ресурс двигате­ля 7800 мото-ч. Эта точка информации выходит за верхнюю границу достоверности. Поэтому она должна быть признана недей­ствительной (выпадающей) и не учитываться в дальнейших расче­тах.

б) Более точно информацию на выпадающие точки проверяют по критерию Ирвина ():

_оп < _т ,

где _оп и _т – опытное и теоретическое значения критерия, соответственно.

При _оп ≤ _т точку считают достоверной; при ._оп > _т точку при­знают выпадающей и исключают из дальнейших расчетов.

Фактическое значение критерия определяется по формуле:

где t_i и t_i-1 любые две смежные точки информации.

Обычно проверку делают для крайних точек сводного ряда информации и резко различающихся друг от друга смежных точек.

В тех случаях, когда после проверки исключают выпадающие точки информации, необходимо заново перестроить статистичес­кий ряд и пересчитать среднее значение и среднее квадратическое отклонение показателя надежности.

Проверим крайние точки информации о доремонтных ресурсах двигателя:

• для наименьшей точки информации _оп1=(1870 - 1500)/1150=0,32.

• для наибольшей точки информации _оп70=(7800 - 5970)/1150=1,59.

По приложению 1 / 3, стр. 757/ находим, что при повторности информации N = 70 и доверительной вероятности  = 0,95 теоретическое значение критерия Ирвина равно _т = 1,05. Следовательно, первую точку информации следует признать достоверной, последнюю точку - выпадающей.

Учитывая, что последняя точка информации выпала, в данном примере после соответствующих пересчетов будем иметь N = 69, = 4084 мото-ч., = 988 мото-ч. Также изменится и вид статистического ряда (см. таблицу 3).

Таблица 3 Статистический ряд после исключения выпавшей точки

Показатели	Интервалы
	1	2	3	4	5	6	7
Границы интервалов, тыс. мото-ч.	1,5 ... 2,2	2,2 ... 2,9	2,9 ... 3,6	3,6 ... 4,3	4,3 ... 5,0	5,0 ... 5,7	5,7 ... 6,4
Опытные частоты, тi	4	1,5	15,5	19	19	5	5
Опытные вероятности, Pi	0,06	0,02	0,22	0,28	0,28	0,07	0,07
Накопленные опытные вероятности, Pi	0,06	0,08	0,30	0,58	0,86	0,93	1,00

5) Выполнение графического изображения опытного распреде­ления показателя надежности. По данным статистического ряда строят гистограмму, полигон и кривую накопленных опытных вероятностей, которые дают наглядное представление об опытном распределении показателя надежности и позволяют ре­шать ряд инженерных задач графическими способами (см. рисунок 1).

6) Определение коэффициента вариации. Коэффициент вариации, характеризующий рассеивание показателя надежности, определяется как:

где t_см - смещение рассеивания показателя надежности, т.е. расстояние от начала ко­ординат до начала рассеивания случайной величины.

Рисунок 1 Графическое изображение опытного распределения

Смещение рассеивания рассчитывают по уравнениям:

• при отсутствии статистического ряда: t_см = t₁ - (t₃-t₁)/2,

• при наличии статистического ряда: t_см = t_н1 - 0,5 t ,

где t₁ и t₃ - первая и третья опытные точки, t_н1 - начало первого интервала статистического ряда.

В нашем случае: t_см = 1500 - 0,5 ∙ 700 = 1150 мото-ч.

Коэффициент вариации: V = 988 / (4084 - 1150) = 0,34.

7) Выбор теоретического закона распределения для выравнива­ния опытной информации. Для выравнивания распределений показателей надежности наиболее широко используют закон нормального распределения (ЗНР) и закон рас­пределения Вейбулла (ЗРВ).

В первом приближении теоретический закон распределения вы­бирают по коэффициенту вариации.

При V < 0,33 выбирают ЗНР, при V > 0,50 - ЗРВ. Если значение коэффициента вариации нахо­дится в интервале 0,33...0,50, то выбирают тот закон распределения, который дает лучшее совпадение с распределением опыт­ной информации.

В нашем случае 0,33 < V < 0,5, поэтому рассмотрим оба закона.

а) Использование для выравнивания распределения опытной инфор­мации закона нормального распределения. Теоретические законы рас­пределения характеризуются дифференциальной (функцией плот­ностей вероятностей) и интегральной (функцией распределения) функциями. Отличительная особенность дифференциальной фун­кции при ЗНР - симметричное рассеивание частных значений показателей надежности относительно среднего значения.

Дифференциальная функция ЗНР описывается уравнением:

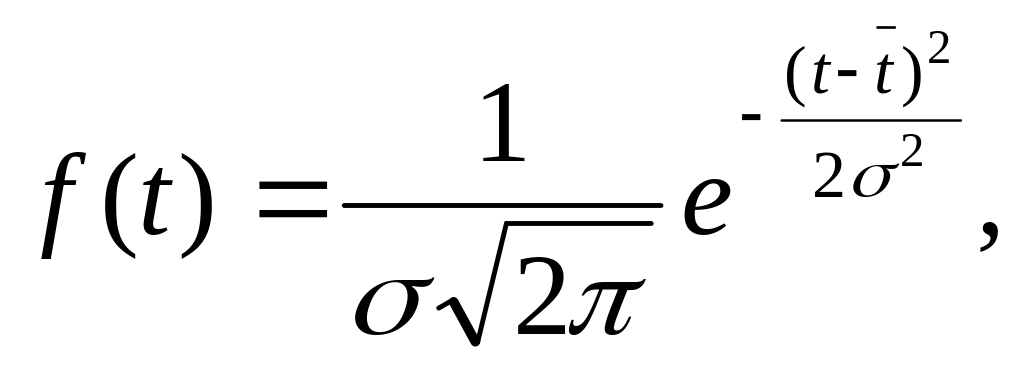
где е — основание натурального логариф­ма (е = 2,718).

Если принять = 0 и σ = 1, то получим выражение для центри­рованной и нормированной дифференциальной функции:

Значения центри­рованной и нормированной дифференциальной функции приводятся в специальных таблицах / 3, стр. 757/.

Для определения дифференциальной функции через центриро­ванную и нормированную функцию используют уравнение:

где t_сi - середина i-го интервала.

Кроме того, следует пользоваться свойством:

Например, значение дифференциальной функции в первом интервале статистического ряда:

Интегральная функция или функция распределения ЗНР:

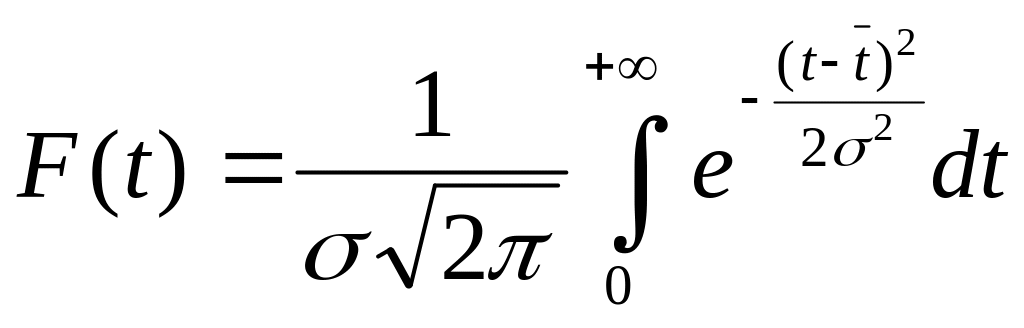
При условии = 0 и σ = 1 получим центрированную и нормиро­ванную интегральную функцию, которая тоже табулирована / 3, стр. 765/.

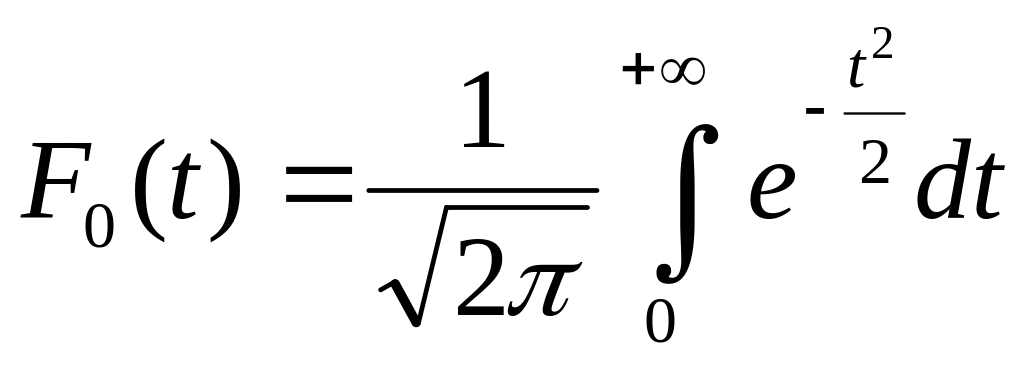
Для определения интегральной функции F(t) через F₀ (t) приме­няют уравнение:

где t_ki - значение конца i-го интервала.

При этом используют также свойство:

Определим значение интегральной функции в первом интервале статистического ряда:

Аналогично рассчитывают значения дифференциаль­ной и интегральной функций по всем интервалам статистического ряда (см. таблицу 4).

Таблица 4 Выбор теоретического закона распределения (ТЗР)

Показатели			Номера интервалов, i								Р, %
			1	2	3	4	5	6	7
Опытные данные статистического ряда		1. Начало интервала, tнi	1,5	2,2	2,9	3,6	4,3	5,0	5,7
		2. Середина интервала, tсi	1,85	2,55	3,25	3,95	4,65	5,35	6,05
		3. Конец интервала,tкi	2,2	2,9	3,6	4,3	5,0	5,7	6,4
		4. Опытная частота, mi	4	1,5	15,5	19	19	5	5
Закон нормального распределения (ЗНР )	Диффер. функция	5 . x=(tсi - t)/
		6. fo(x
		7. f(ti)=t·fo(x)/	0.02	0.09	0.19	0.28	0.24	0.13	0.04
	Интегр. функция	8 . x=(tкi - t)/
		9. F(ti)=F(x	0.03	0.11	0.31	0.59	0.82	0.95	0.99
	Критерий Пирсона	10. mтi=N(F(ti)-F(ti-1))
		11. mi по укрупн. ряду(3)	5,5		15,5	19	19	5	5
		12. mтi по укрупн. ряду	7,6		13,8	19,3	15,9	9,0	2,8
		13. (mi-mтi)2/mтi
Закон распределения Вейбулла (ЗРВ)	Диффер. функция	14. (tсi - tсм)/а(4)
		15. x=fтабл((tсi - tсм)/а
		16. f(ti)=t·fтабл(x)/а	0.02	0.11	0.20	0.24	0.21	0.12	0.05
	Интегр. функция	17. x=(tкi - tсм)/а
		18. F(ti)=F(x	0.03	0.13	0.33	0.58	0.81	0.95	0.99
	Критерий Пирсона	19. mтi=N(F(ti)-F(ti-1))
		20. mi по укрупн. ряду	5,5		15,5	19	19	5	5
		21. mтi по укрупн. ряду	9,0		13,8	17,3	15,9	9,7	2,8
		22. (mi-mтi)2/mтi

Примечания:

1. Центрированная (нормированная) дифференциальная функция ЗНР имеет свойство: f_о(-х)=f_о(+х)

2. Центрированная (нормированная) интегральная функция ЗНР имеет свойство: F_о(-х)=1-F_о(+х)

3. Условия укрупнения ряда (объединения интервалов): m_тi5; i >4.

4. Смещение рассеивания: t_см=t_н1-0,5t, если t_см < 0, то принимается t_см = 0.

б) Использование для выравнивания распределения опытной инфор­мации закона распределения Вейбулла. Дифференциальную функ­цию или функцию плотности вероятностей определяют при законе распределения Вейбулла по уравнению:

где а и b - параметры масштаба и формы ЗРВ, соответственно.

Параметр формы b определяют по специальным таблицам / 3, стр. 765/ в зависимости от коэффициента вариации. Из этой же таблицы выбираются коэффициенты К_в и С_в.

Для нашего случая при V = 0,34: b = 3.2, К_в = 0,90 и С_в = 0,31.

Параметр масштаба а рассчитывают по одному из уравнений:

a =( - t_см) / К_в или a =  / С_в .

В нашем случае: а = (4084 - 1150) / 0,90 = 3260 мото-ч.

Дифференциальную функцию ЗРВ можно определить и с помощью специальных таблиц / 3, стр. 766/. При этом используют уравнение:

где t_см - смещение.

Найдем дифференциальную функцию в первом интервале ста­тистического ряда:

Интегральная функция или функция распределения закона Вейбулла описывается формулой:

Интегральную функцию ЗРВ также можно определить с помощью специальных таблиц / 3, стр. 766/. При этом используют уравнение:

где t_ki — значение конца i - гo интервала.

Например, интегральная функция в первом интервале статисти­ческого ряда:

Аналогично определяются значения дифференциальной и интег­ральной функций в остальных интервалах статистического ряда (см. таблицу 4).

8) Оценка совпадения опытного и теоретического законов распре­деления показателей надежности по критерию согласия. При обработке информации по показателям надежности наиболее часто применяется критерий со­гласия Пирсона (χ²), определяемый по уравнению:

где n_y - число укрупненных интервалов; m_i — опытная час­тота в i - ом интервале статистического ряда; m_Ti - теоретическая частота в i - ом ин­тервале.

Теоретическая частота определяется как:

m_Ti = N [ F(t _i) - F(t _{i - 1})],

где N — число точек информации; F(t _i) и F(t _{i - 1}) - значения интегральной функции для i - го и (i -1) - го интервалов статистического ряда.

Для определения χ² строят укрупненный статистический ряд, соблюдая условие: n_y > 4, m_i  5. При этом допускается объединение соседних интервалов, в которых m_i < 5.

В нашем случае m₁ = 4 и m₂ = 1,5 , по­этому первый и второй интервалы статистического ряда следует объединить. Опытная частота в объединенном интервале будет равна сумме частот объединяемых интервалов. В остальных интервалах статис­тического ряда опытные частоты больше пяти, поэтому эти интер­валы оставляем без изменения (см. таблицу 4).

Определим значения критерия согласия Пирсона. При законе нормального распределения:

При законе распределения Вейбулла:

Для дальнейших расчетов выбирают тот закон распределения, у которого меньше значение критерия Пирсона. В нашем примере, применительно к доремонтным ресурсам двигателя, более приемлемым является за­кон нормального распределения.

Кроме того, пользуясь критерием согласия χ², по специальной таблице можно определить вероятность совпадения (Р, %) опытных и теоретичес­ких распределений / 3, стр. 768 /. Для входа в таблицу определяем номер строки (число степеней свободы):

R = n_y – K,

где n_у- число интервалов в укрупненном статистическом ряду;

К - число обяза­тельных связей.

Для рассматриваемых законов распределения число обязательных связей равно трем: две связи – два параметра распределения (для ЗНР - и б, для ЗРВ – a и b) и третья связь ∑Р = 1.

Таким образом, в нашем случае R = 6 – 3 = 3. По третьей строке таблицы определяем, что вероят­ность совпадения для ЗНР составляет около 18 %, а для ЗРВ - менее 10 %.

9) Определение доверительных границ рассеивания одиночного и среднего значений показателя надежности. Площадь под дифференциальной кривой, ограниченная осью абсцисс и доверительными границами характеризует сте­пень доверия расчета и гарантирует заданную вероятность попадания показателя надежности в соответствующий интервал его значе­ний. Поэтому ее называют доверительной вероятностью.

Интервал, в который при за­данной доверительной вероят­ности ß попадает 100 % общего числа объектов совокупности N, называют доверительным ин­тервалом I_ß. Границы, в которых может колебаться значение одиночно­го показателя надежности при заданной ß, называют нижней t_ß^н и верхней t_ß^в доверительны­ми границами.

Положение доверительных границ и доверительный интер­вал зависят от доверительной вероятности и закона распределения одиночного или среднего значения показателя надежности.

а) Определение доверительных границ рассеивания при законе нор­мального распределения. Для определения доверительных границ рассеивания одиночного значения показателя надежности при ЗНР вначале находят абсолютную ошибку:

е_ß = t_ß σ ,

где t_ß - коэффициент Стьюдента.

Нижняя доверительная граница:

t_ß^н = - t_ß σ

Верхняя доверительная граница:

t_ß^в = + t_ß σ,

Доверительный интервал:

I_ß = t_ß^в - t_ß^н

Для нашего примера ко­эффициент Стьюдента при ß = 0,90 : t_ß = 1,67. Тогда:

• нижняя доверительная граница: t_ß^н = 4084 -1,67 ∙ 988 = 2434 мото-ч.;

• верхняя доверительная граница: t_ß^в = 4084 + 1,67 ∙ 988 = 5734 мото-ч.;

• доверительный интервал: I_ß = 5734 - 2434 = 3300 мото-ч.

Расчетная схема и физический смысл доверительных границ среднего значения показателя надежности те же, что и для одиноч­ного показателя. Разница заключается в значении среднего квадратического отклонения.

Среднее квадратическое отклонение рассеивания среднего зна­чения показателя надежности:

где N - число точек информации, по которому определено среднее значение пока­зателя надежности.

Нижняя доверительная граница среднего значения показателя надежности:

Верхняя доверительная граница среднего значения показателя надежности:

Доверительный интервал среднего значения показателя надеж­ности:

I_ß = t_ß^в - t_ß^н

Для приведенного примера по обработке информации по ресур­су двигателя получаем (коэффициент Стьюдента t_ß = 1,67):

• нижняя доверительная граница: t_др^н = 3885 мото-ч.;

• верхняя доверительная граница: t_др^в = 4283 мото-ч.;

• доверительный интервал: I_ß = 4283 - 3885 = 398 мото-ч.

б) Определение доверительных границ при законе распределения Вей­булла. Доверительные границы рассеивания одиночного значения показателя надежности при ЗРВ определяют по уравнениям:

где H_к^в - квантиль закона распределения Вейбулла / 3, стр. 769 /.

Доверительный интервал: I_ß = t_ß^в - t_ß^н

Для рассматриваемого примера при доверительной вероятности  = 0,90:

• нижняя доверительная граница: t_др^н = H^в_к ((1 - 0,90) / 2) ∙ 3260 + 1150 = 0,39 ∙ 3260 + 1150 = 2421 мото-ч.;

• верхняя доверительная граница: t_др^в = H^в_к ((1 + 0,90) / 2) ∙ 3260 + 1150 = 1,41 ∙ 3260 + 1150 = 5747 мото-ч.;

• доверительный интервал: I_ß = 5747 - 2421 = 3326 мото-ч.

Доверительные границы рассеивания среднего значения показа­теля надежности при ЗРВ определяют по уравнениям:

где r₁ и r₃ - коэффициенты распределения Вейбулла /3, стр. 768/, зависящие от доверительной вероятности  и повторности информации N.

Доверительный интервал среднего значения показателя надеж­ности:

I_ß = t_ß^в - t_ß^н

Для нашего случая (r₁ = 1,23; r₃ = 0,83):

10) Определение абсолютной и относительной предельных оши­бок оценок характеристик показателя надежности. Наибольшая абсолютная ошибка переноса опытных характеристик показателя надежности при заданной доверительной вероятности равна по значению е_β в обе стороны от среднего значения показателя надеж­ности.

Относительная предельная ошибка:

Для нашего примера при законе нормального распределения: δ_β = [(4283 - 4084) / 4084] ∙ 100 = 4,9 %.

11) Построение графиков дифференциальной и интегральной функций для исследуемого показателя надежности по выбранному закону распределения. По значениям f(t) и F(t) выбранного закона распределения могут быть пост­роены графики дифференциальной и интегральной функций. Дифференциальная кривая заменяет поли­гон опытного распределения, а интегральная - кривую накопленных опыт­ных вероятностей (см. рисунок 2). Эти графики в дальнейшем можно использовать при решении прикладных задач.

Например, по интегральной функции можно определить число отказавших двигателей не только в интервалах статистичес­кого ряда, но и в любом требуемом интервале наработки.

Допустим, необходимо определить число двигателей, отказавших в ин­тервале наработки 4300...4850 мото-ч. Для этого необходимо по графику интегральной функции определить значения F(t) в начале и в конце этого интервала и их разницу умножить на общее число двигателей:

Тогда

N_от.дв.= F (4300…4850) ∙ N = 0, 19 ∙ 69 = 13 двигателей.

Рисунок 2 Графики дифференциальной и интегральной функции распределения доремонтных ресурсов двигателя согласно выбранному закону распределения (ЗНР)