Определение оптимальной величины закупаемой партии

Количество закупаемых в год партий	1	2	3	4	5
Величина партии, кг	20000	10000	6667	5000	4000
Среднегодовой запас, кг	10000	5000	3333	2500	2000
Стоимость среднегодового запаса, тыс. руб.	100000	50000	33333	25000	20000
Издержки по складированию, тыс. руб.	20000	10000	6667	5000	4000
Издержки по обслуживанию закупок, тыс. руб.	1250	2500	3750	5000	6250
Издержки по складированию и обслуживанию закупок (всего), тыс. руб.	21250	12500	10417	10000	10250

Расчеты показывают, что издержки по складированию сокращаются, а издержки по обслуживанию закупок возрастают при увеличении числа закупок в год. Оптимальное годовое число закупок в нашем примере равно четырем, поскольку при этом показателе сумма издержек по складированию и обслуживанию закупок является наименьшей (10000 руб.).

При расчетах, подобных приведенному в таблице 3, необходимо использовать такое количество альтернативных показателей числа закупок, которое обеспечивало бы включение в этот ряд и оптимального количества закупаемых партий.

Рис. 9 иллюстрирует расчеты, приведенные в табл. 3. Однако при построении графика мы дополнительно включили показатель величины закупаемой партии 2000 кг. Оптимальное значение величины закупаемой партии находим в нижней точке кривой издержек по складированию и обслуживанию закупок. Оно соответствует значению величины закупаемой партии, которое находим в точке пере­сечения кривой издержек по складированию с кривой издержек по обслуживанию закупок.

Однако расчет оптимальной величины закупаемой партии можно также производить с помощью универсальной формулы:

q — годовой объем закупаемых товаров в соответствующих единицах измерения (шт, кг и т. д.);

о — издержки по обслуживанию закупок в расчете на 1 партию;

ц — цена франко-склад покупателя за единицу товара; С,— издержки на складирование в процентах от стоимости среднегодового производственного запаса. Выражается в виде десятичной дроби, например 10%-0,10;

Q — оптимальная величина закупаемой партии.

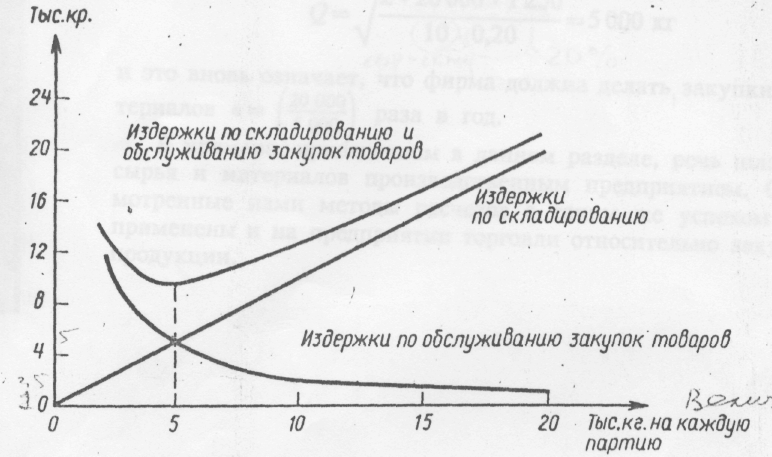
Рис.9. Оптимальная величина закупаемой партии

Данная формула часто называемая формулой Уильсона.

Подставив значения из нашего примера, получим следую- щее:

,

и это вновь означает, что фирма должна делать закупки сырья и материалов раза в год по 5000 тыс. кг.

В примере, приведенном в данном разделе, речь шла о закупках сырья и материалов производственным предприятием. Однако рассмотренные нами методы расчетов с таким же успехом могут быть применены и на предприятии торговли относительно закупок готовой продукции.

3.2.2. Задача оптимизации транспортных расходов (т-задача)

При решении задач оптимизации транспортных процессов в качестве критерия оптимальности в основном используется минимум провозной платы, который успешно применяется для сокращения транспортных расходов поставщиков и потребителей продукции и обеспечивает получение плана перевозок, оптимальных с точки зрения экономических показателей предприятий.

При решении задач оптимизации транспортных процессов возникает проблема получения информации о пунктах производства и пунктах потребления продукции. На первый взгляд получить информацию о пунктах производства является простым делом. В действительности приходится сталкиваться с трудностями, связанными со сроками ввода в эксплуатацию новых мощностей, которые иногда не соблюдаются. Трудности возникают при получении информации о потребителях продукции. Сбор информации о всех потребителях продукции настолько трудоемок, что использование всей информации не позволяет уложиться в сроки, отведенные для составления планов перевозок. По этой причине приходится объединять (агрегировать) потребителей по транспортному признаку (по железнодорожным участкам или транспортным узлам) или по административному делению.

Сложной является проблема определения однородности продукции. Однородность продукции необходимо оценивать не только с точки зрения ее качества, но и по способу транспортировки. Так, некоторые продукты можно перевозить в таре или наливом в цистернах, в специальной упаковке или в контейнерах и т.п. В этих случаях затраты на транспортировку одного и того же продукта будут различными, и по этой причине продукт нельзя считать однородным.

Основной математической моделью, используемой для решения задач оптимального прикрепления потребителей к поставщикам и составления оптимальных планов перевозок, является так называемая транспортная задача линейного программирования (Т-задача).

В общем виде данная задача имеет следующую формулировку:

В m пунктах А₁, А₂, …, А_m производится некоторый однородный продукт, причем объем производства в пункте А_i составляет a_i единиц (i=1, 2, …, m).

Указанный продукт потребляется в n пунктах В₁, В₂, …, В_n, а объем потребления в пункте В_j составляет b_j единиц (j=1, 2, …, n).

Известны транспортные расходы по перевозке единицы продукции из пункта А_i в пункт В_j, которые равны С_{i j} и приведены в матрице транспортных р асходов С:

С₁₁ С₁₂…С_1n

C = C₂₁C₂₂…C_2n

. . . . . . . . . .

C_m C_m2…C_mn

Требуется составить такой план перевозок, при котором весь продукт вывозится из пунктов производства, и удовлетворяются запросы всех потребителей, а общая величина транспортных издержек является минимальной.

Для составления математической модели данной задачи принимаем количество продукта, перевозимого из пункта А_i в пункт В_j равным X_ij . В этом случае поставленные нами условия можно записать следующим образом.

Определить множество переменных X_ij ≥ 0 (I = 1, 2, …, m, j = 1, 2, …, n), удовлетворяющих условиям

а_i (1)

b_i (2)

при которых целевая функция достигает минимума

Z = (3)

Условие, необходимое и достаточное для разрешимости данной задачи, сводится к балансу

(4)

Условие (1) характеризует вывоз продукции из всех пунктов производства, а условие (2) означает полное удовлетворение спроса во всех пунктах потребления.

Переменные нумеруют с помощью двух индексов, а набор X_ij , удовлетворяющий условиям (1) и (2), записывают в виде матрицы.

Х₁₁ Х₁₂ … Х_1n

Х = Х₂₁ Х₂₂ … Х_2n

....…………….

Х_m1 Х_m2 … Х_mn

Матрицу Х называют планом перевозок Т-задачи, а переменные X_ij – перевозками. План Х_опт, при котором целевая функция (3) минимальная, называется оптимальным планом.

Рассмотрим пример составления плана перевозок однородного продукта с трех пунктов отправления в четыре пункта назначения при следующих исходных данных:

Ресурсы поставщиков: а₁ =170, а₂ = 250, а₃ =180;

Фонды потребителей: b₁ =150, b₂ = 230, b₃ =160, b₄ = 60

Матрица транспортных расходов дана в табл. 5.

Таблица 5

Матрица транспортных расходов

Поставщик	Потребитель
	1	2	3	4
1 2 3	С11=3 C21=6 C31=5	C12=5 C22=4 C32=4	C13 =6 С23=7 С33=6	С14=2 С24=5 С34=5

В этой задаче ограничения можно записать следующим образом:

а) по ресурсам поставщиков

Х₁₁ + Х₁₂ + Х₁₄ = 170,

Х₂₁ + Х₂₂ + Х₂₄= 250,

Х₃₁+ Х₃₂ + Х₃₄ = 180,

б) по фондам потребителей

Х₁₁ + Х₂₁ + Х₃₁ = 150,

Х₁₂ + Х₂₂ + Х₃₂ = 230,

Х₁₃+ Х₂₃ + Х₃₃ = 160,

Х₁₄ + Х₂₄ + Х₃₄ = 60

в) при условиях не отрицательности поставок

Х₁₁ ≥ 0, Х₁₂ ≥ 0, … Х₃₄ ≥ 0.