Раздел 3 алгоритмы циклической структуры
3.1. Решение типовых задач
Циклический алгоритм - это алгоритм, который предусматривает многократное повторение действий в одной и той же последовательности по одним тем - же математическим зависимостям, но при разных значениях некоторой специально изменяемой величины.
Многократное выполнение некоторой группы повторяющихся оператором называют телом цикла.
Специально изменяемый по заданному закону параметр, входящий в тело шипи, называют переменной цикла.
Переменная цикла используется для подготовки очередного повторения цикла и отслеживания условий его окончания. Во время выполнения тела ник па параметры переменной цикла изменяются в интервале от начального до конечного значения с заданным шагом.
При организации циклических вычислений необходимо предусмотреть следующее:
1) начальное значение переменной цикла;
2) конечное значение переменной цикла; 3) закон изменения переменной цикла перед каждым новым его повторением, т.е. необходимо предусмотреть шаг цикла.
Цикл называется простым, если в его теле нет разветвлений и других не встроенных циклов.
Цикл называется сложным, если в его теле есть разветвления и (или) другие встроенные в цикл циклы.
Цикл называется детерминированным, если в нем число повторений заранее известно из исходных данных или определено в ходе решения задачи.
Цикл называется итерационным, если в нем число повторений неизвестно из исходных данных и не определено по ходу решения задачи.
В зависимости от нахождения условия итерационные циклы могут бьгп1 организованы двумя путями:
как циклы с предусловием (условие размещено перед телом цикла);
как циклы с постусловием (условие размещено после тела цикла). Операторы, с помощью которых можно осуществить цикл:
IF (с использованием оператора GOTO) WHILE...WEND DO...LOOP FOR ...NEXT |
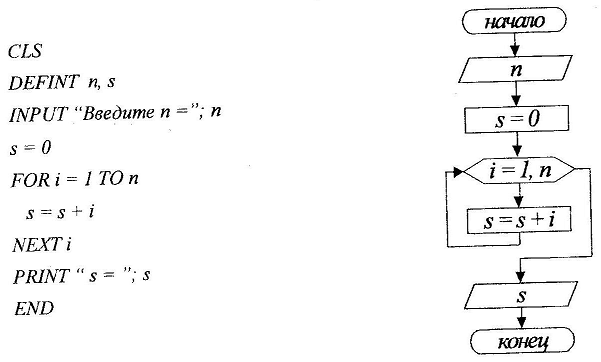
73. Дано натуральное число n. Найти сумму первых n членов натурального ряда.
Решение:
74. Вычислить n!, где n – натуральное число.
Решение:
75. Вычислить сумму:
:
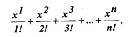
Где n – натуральное число, x – действительное.
Решение:
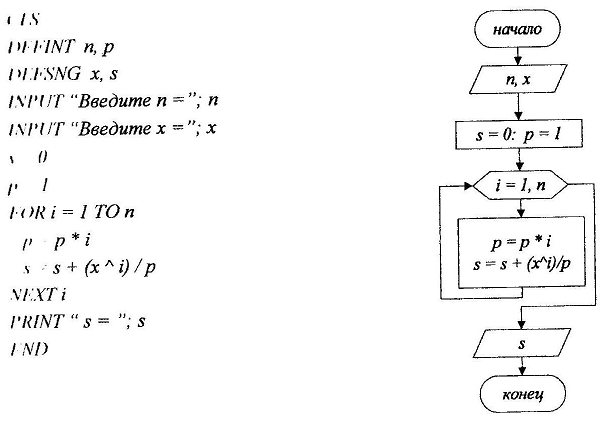
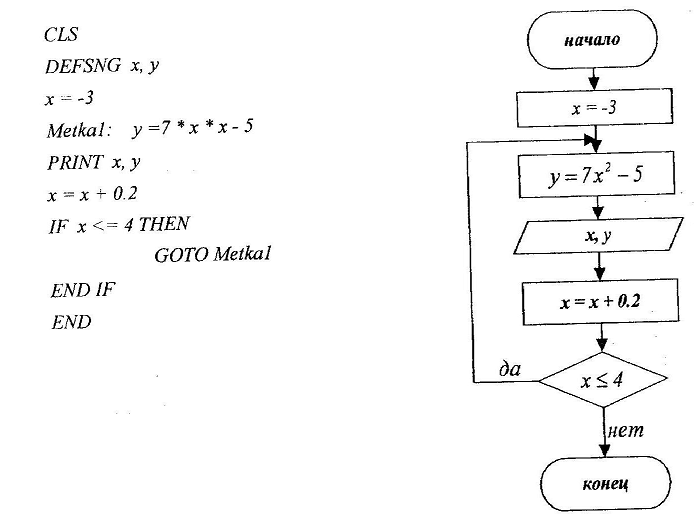
76. Вычислить множество значений функции
у = 7х2 -5,
где х принадлежит промежутку [-3,4] с шагом 0.2 с помощью оператора IF
Замечание: организовать цикл с постусловием.
Решение:
77. Вычислить множество значений функции
у = 7х2 -5,
где х принадлежит промежутку [-3,4] с шагом 0.2 с помощью оператора IF
Замечание: организовать цикл с постусловием.
Р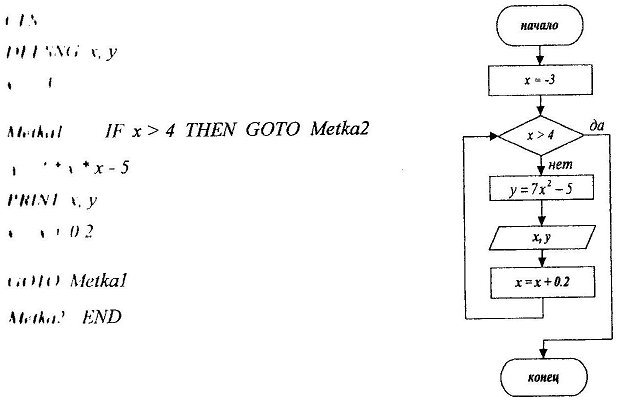
ешение:
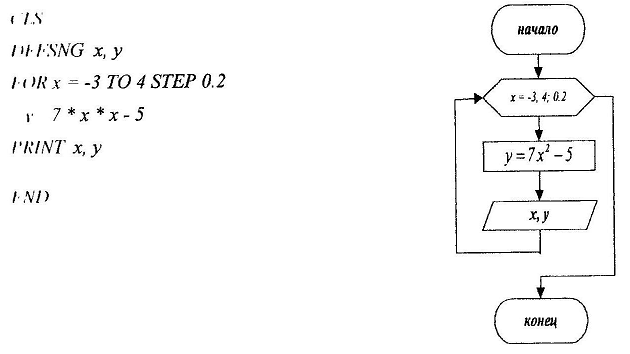
78. Вычислить множество значений функции
у = 7х2 -5,
где х принадлежит промежутку [-3,4] с шагом 0.2 с помощью оператора FOR…NEXT
Замечание: организовать цикл с постусловием.
Решение:
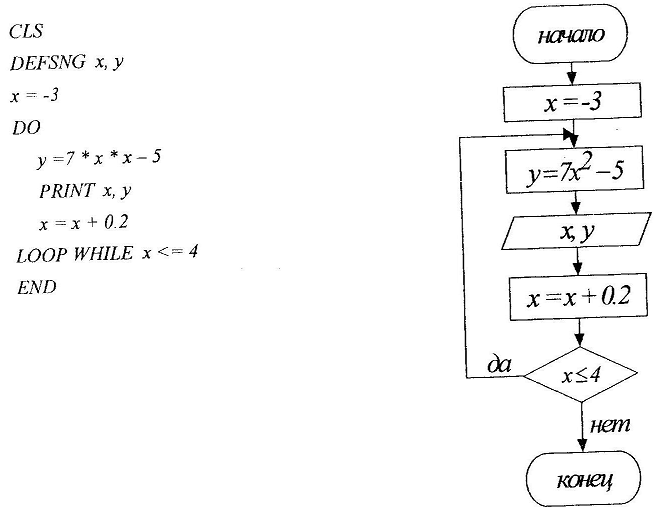
79. Вычислить множество значений функции
у = 7х2 -5,
где х принадлежит промежутку [-3,4] с шагом 0.2 с помощью оператора DO…LOOP
Замечание: организовать цикл с постусловием
Решение:
80. Вычислить множество значений функции
у = 7х2 -5,
где х принадлежит промежутку [-3,4] с шагом 0.2 с помощью оператора DO…LOOP
Замечание: организовать цикл с постусловием
Решение:
