Перевод дробных чисел

• Справа налево, с последней цифры от запятой расставляем разряды начиная с нулевого;

• Слева направо, с первой цифры после запятой расставляем разряды начиная с –1;

• Берем 1 цифру, умножаем ее на основание системы счисления(на 2) в степени разряда;

• Прибавляем вторую цифру умножаем ее на основание системы счисления в степени разряда и т. д .

Пример

1. Разряды 3 2 1 0 1

Число 1 0 1 1, 12= 1  23 + 0  22 + 1  21 + 1  20

+ 1  2 – 1=11,5

2. 0,1101₂ = 1  2^-1 + 1  2^-2 + 0  2^-3 +1  2^-4 =

= 0,5 + 0,25 + 0 + 0,0625 = 0,8125.

3. 1000011111,0101₂=1  2⁹ + 1  2⁴ + 1  2³ + 1  2² + 1  2¹ +

+ 1  2⁰ + 2^-2 + 1  2^-4 = 512 + 16 + 8 + 4 + 2 + 1 +

+ 0,25 + 0,0625 = 543,3125₁₀.

Перевод из восьмеричной системы счисления

в десятичную

Алгоритм перевода аналогичен переводу из двоичной системы счисления в десятеричную.

Примеры

₁₎

2) 1216,04₈=1  8³ + 2  8² + 1  8¹ + 6  8⁰ + 4  8^-2 =

= 512 + 128 + 8 + 6 + 0,0625 = 654,0625₁₀.

Перевод из шестнадцатеричной системы счисления

в десятичную

Алгоритм перевода аналогичен переводу из двоичной системы счисления в десятеричную.

Примеры

1. 29A,5₁₆ = 2  16² + 9  16¹ + 10  16⁰ + 5  16^-1 =

512 + 144 + 10 + 0,3125 = 656,3125₁₀ .

2. 0,D8D16 = 13  16^-1 + 8  16^-2 + 13  16^-3 =

=13  0,0625 + 8  0,003906 + 13  0,000244 = 0,84692.¶

3. )

Перевод из десятичной системы счисления

Целая часть

1. Последовательно делить целую часть десятичного числа на основание, пока десятичное число не станет равно нулю.

2. Полученные при делении остатки являются цифрами нужного числа. Число в новой системе записывают, начиная с последнего остатка.

Дробная часть

1. Дробную часть десятичного числа умножаем на основание системы, в которую требуется перевести. Отделяем целую часть. Продолжаем умножать дробную часть на основание новой системы, пока она не станет равной 0.

2. Число в новой системе составляют целые части результатов умножения в порядке, соответствующем их получению.

Перевод произвольных чисел

Перевод произвольных чисел, то есть чисел, содержащих целую и дробную части, осуществляется в два этапа. Отдельно переводится целая часть, отдельно – дробная. В итоговой записи полученного числа целая часть отделяется от дробной запятой.

Перевод из десятичной системы счисления в двоичную

Целая часть

Перевести 19 в двоичную систему

Пример

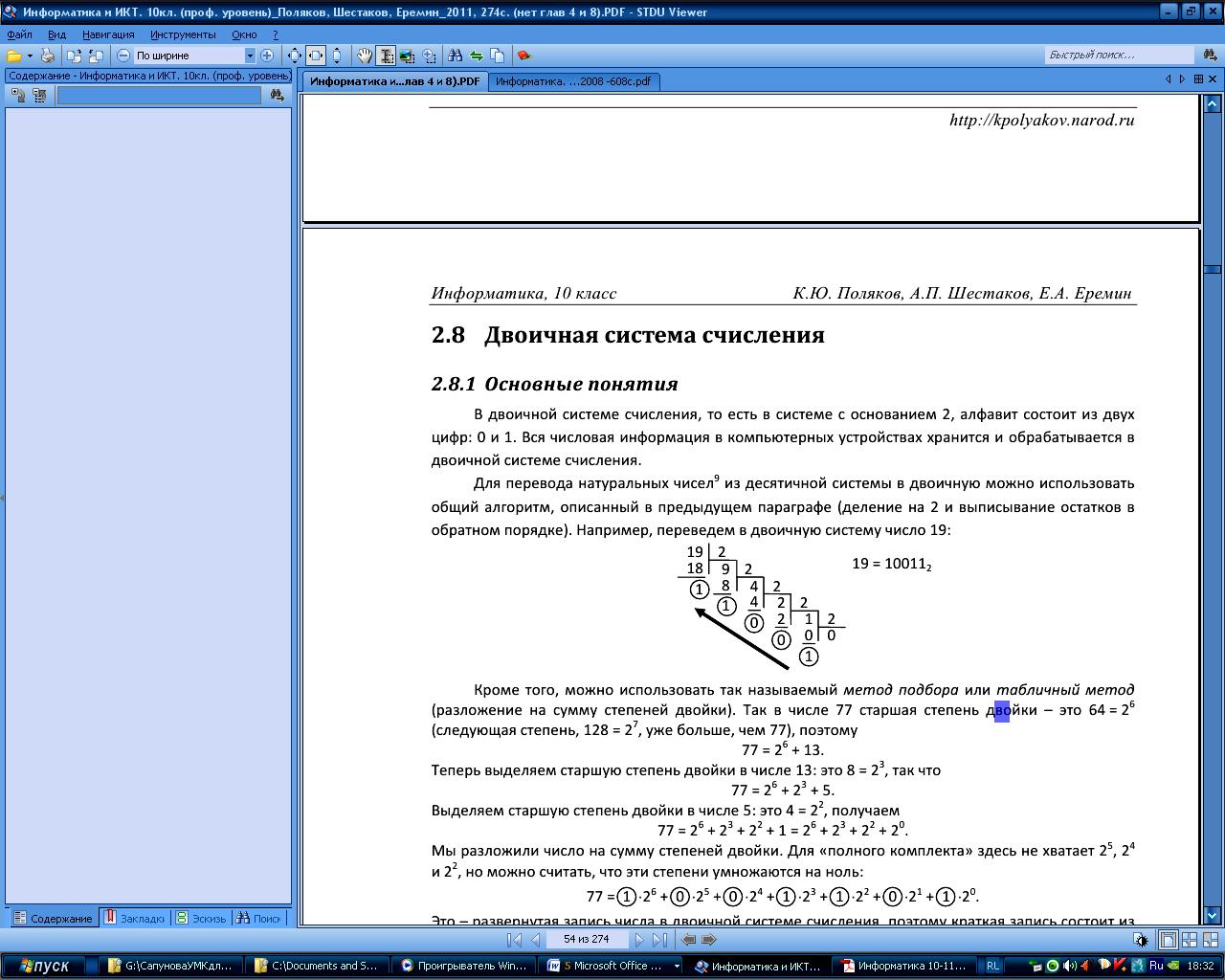
Дробная часть

1) Перевести десятичную дробь 0,5625₁₀ в двоичную систему счисления.

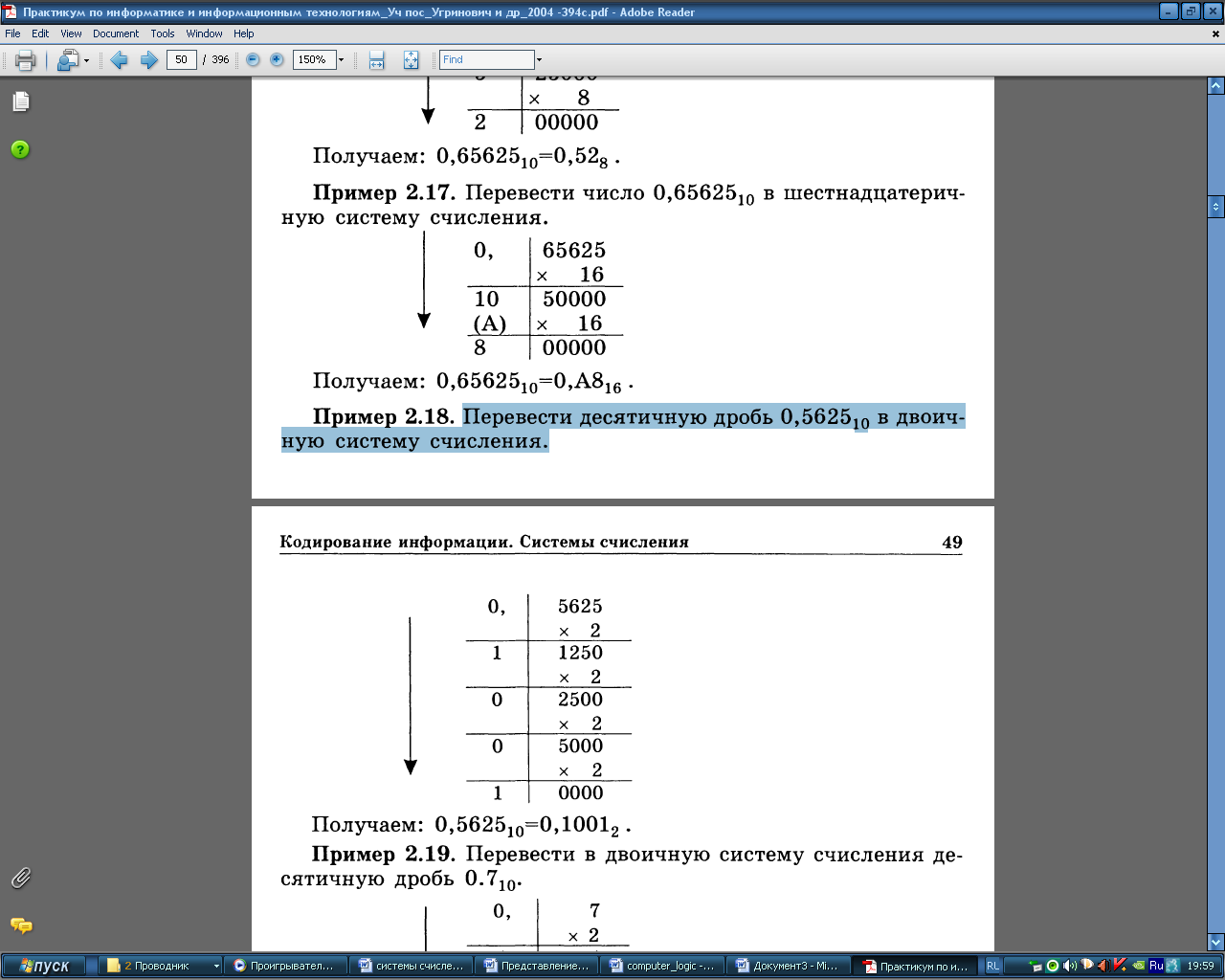
Получаем: 0,5625₁₀=0,1001₂ .

2)	Вычисления	Целая часть	Дробная часть
	0,8125  2 = 1,625		0,625
	0,625  2 = 1,25		0,25
	0,25  2 = 0,5		0,5
	0,5  2 = 1		0

Таким образом, 0,8125 = 0,1101₂.

Перевод из десятичной системы счисления

в восьмеричную

Целая часть

1)Перевести 100 в восьмеричную систему счисления

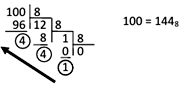
Проверка

разряды → 2 1 0

1 4 4₈ = 1 ⋅ 8² + 4 ⋅ 8¹ + 4 ⋅ 8⁰ = 64 + 4 ⋅ 8 + 4 = 100.

2) Перевести десятичное число 173₁₀ в восьмеричную систему счисления:

Получаем: 173₁₀=255₈ .

Дробная часть

1. Перевести число 0,65625₁₀ в восьмеричную систему счисления.

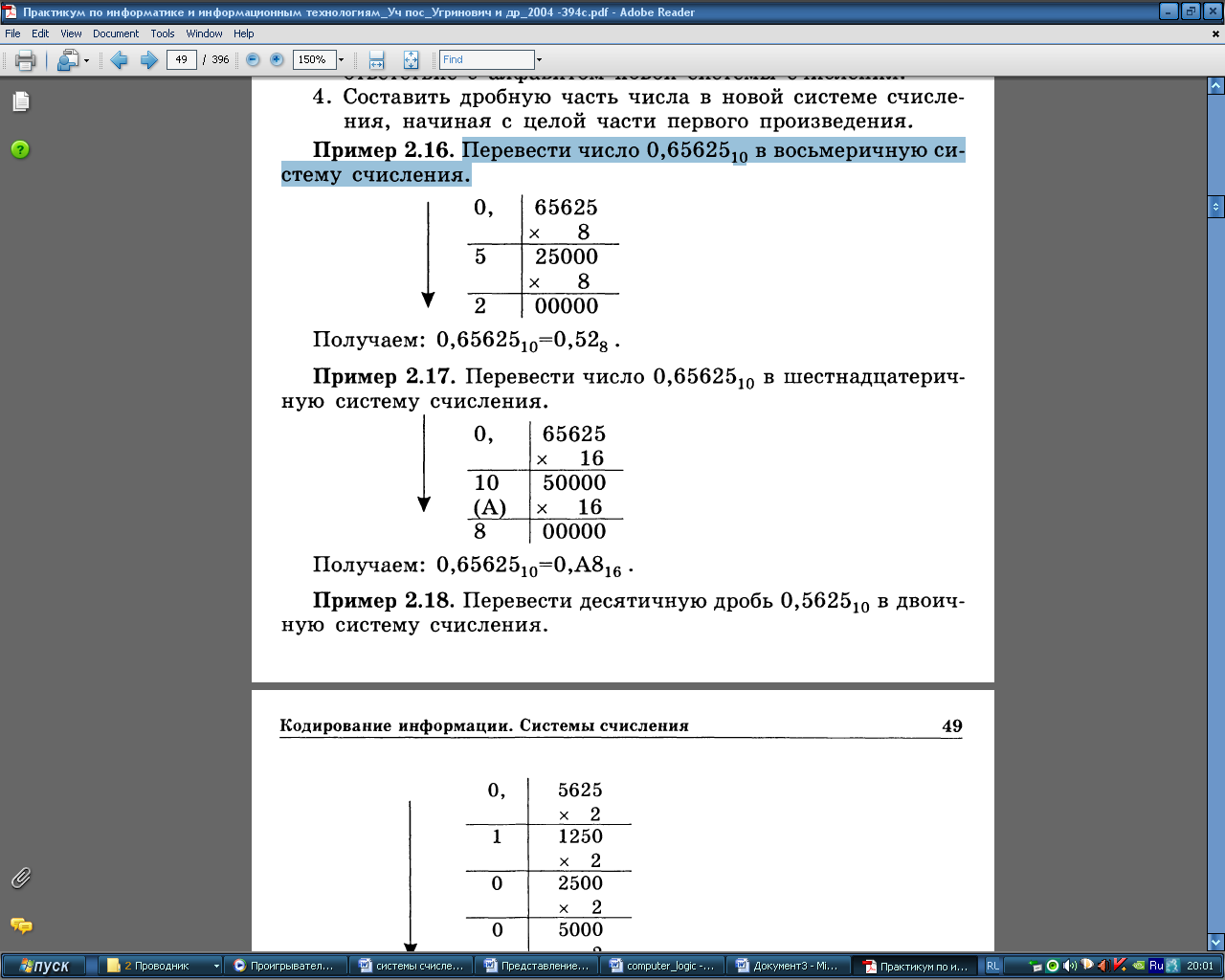
Перевод произвольных чисел

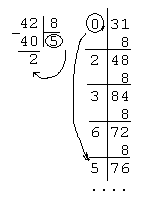
1) перевести в 8-сс = 52,2365₈

Перевод из десятичной системы счисления

в шестнадцатеричную

Целая часть

Для перевода чисел из десятичной системы в шестнадцатеричную используют алгоритм деления на 16 и взятия остатков. Важно не забыть, что все остатки, большие 9, нужно заменить на буквы.

Примеры

1) Перевести десятичное число 173₁₀ в шестнадцатеричную систему счисления:

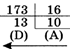
Получаем: 173₁₀=AD₁₆.

2)

3)

Для проверки значение каждой цифры умножают на 16 в степени, равной ее разряду, и полученные значения складывают:

Разряды → 2 1 0

1 B C₁₆ = 1 ⋅ 16² + 11 ⋅ 16¹ + 12 ⋅ 8⁰ = 256 + 176 + 12 = 444.