2.2. Отсечение невыпуклым многоугольником без самопересечений.

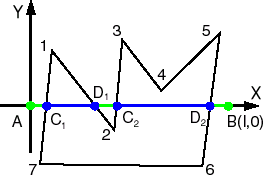
Рис. 5. Отсечение невыпуклым многоугольником.

На Рис. 5 результатом отсечения отрезка AB являются отрезки C₁D₁ и C₂D₂

Алгоритм в этом случае по сути аналогичен приведенному выше алгоритму для отсечения выпуклым многоугольником.

Создадим список точек пересечения Ax c многоугольником:

Для каждого ребра возможны 4 случая:

а) обе его вершины лежат выше или ниже Ax (например, на Рис. 5 3-4): ничего не заносим в наш список
б) его вершины лежат по разные стороны от Ax (например, на Рис. 5 1-2): заносим в список точку пересечения
в) ребро лежит на Ax ничего не заносим в наш список
г) вершина лежит на Ax г 1) если другие вершины смежных ребер лежат по одну сторону от Ax: ничего не заносим в список
г 2) если другие вершины смежных ребер лежат по разные стороны от Ax: заносим эту вершину в список,

Далее, список точек пересечения должен быть отсортирован по возрастанию (их количество обязано быть четным , т.к. для каждого "входа" в многоугольник должен существовать и "выход"):

x1 < x2 < x3 < x4 и т.д., тогда искомый отрезок - это :

[0,l]  ([x1,x2]  [x3,x4]  [x5,x6] …) (т.к. нечетная точка - всегда точка "входа", а четная - точка "выхода")

2.3. Комбинированный алгоритм Кузьмина. [Kuzmin, 1995]

Алгоритм Кузьмина является модификацией алгоритма Брезенхема, позволяющей сразу решать задачу и отсечения по прямоугольнику, и рисования отрезка. Ниже приводятся основные идеи алгоритма. Точное описание можно найти в [Kuzmin, 1995]

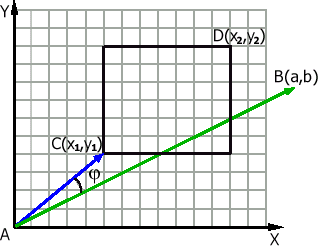
Рис. 6. Определение точки входа.

Первым делом проверим, нужно ли рисовать что-либо вообще (например, с помощью идеи алгоритма Сазерленда-Кохена).

Если нужно рисовать, то перейдем к канонической системе координат Axy, тогда наш отсекающий прямоугольник можно задать координатами своих левого нижнего C(x₁,y₁) и правого верхнего D(x₂,y₂) углов. Тогда в зависимости от знака векторного произведения [AB  AC] (т.е. a*y₁-b*x₁) отрезок AB пересекает:

1. горизонтальную границу (случай на Рис. 6)

[AB  AC] >0

2. вертикальную границу

[AB  AC] <0

Найдем для двух случаев начальные значения x, y и e₀ , далее будем действовать по алгоритму Брезенхема. Ради целочисленности алгоритма все переменные, связанные с e, по-прежнему домножены на 2a.

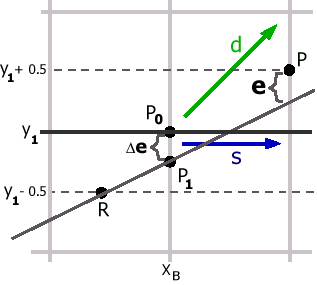
1) Горизонтальный случай (Рис. 7).

Рис. 7. Горизонтальный случай.

В этом случае y=y1; а вот x надо найти. Для этого будем следовать алгоритму Брезенхема, как если бы мы рисовали без отсечения, тогда первая точка с координатой y1 будет нарисована тогда, когда для некоего x=xв будет выполнено следующее: xR  (xв , xв+1] , где R - точка пересечения нашего отрезка с прямой y= y1- 0.5 xв= *(y1 - )+1= (a*(2*y1-1))/(2*b) +1 (Деление целочисленное (т.е. возвращает целую часть частного) !!) e=(yP0- yP1)*2a= (y1 - *xв)*2a= =2*(a*y1- b*xв) e0=2b - a - e=2b - a- 2*a*y1+ 2*b*xв= = 2b*(xв+1) - a*(2*y1+1)

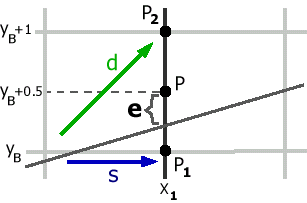
2) Вертикальный случай (Рис. 8).

Рис. 8. Вертикальный случай.

В этом случае x=x1; а вот y надо найти исходя из значения e0 Пусть yв=x1*(b/a)=(x1*b)/a (Деление целочисленное (т.е. возвращает целую часть частного) !!) e0=( *x1-yв- )*2a = 2b*x1-a*(2*yв+1) Тогда возможны 2 варианта: e0 < 0 тогда первая точка - P1 (x=x1 , y= yв) и e0= e0 + 2*b e0  0 тогда первая точка - P2 (x=x1 , y= yв+1) и e0= e0 + 2*b-2*a

Условием выхода из алгоритма является:

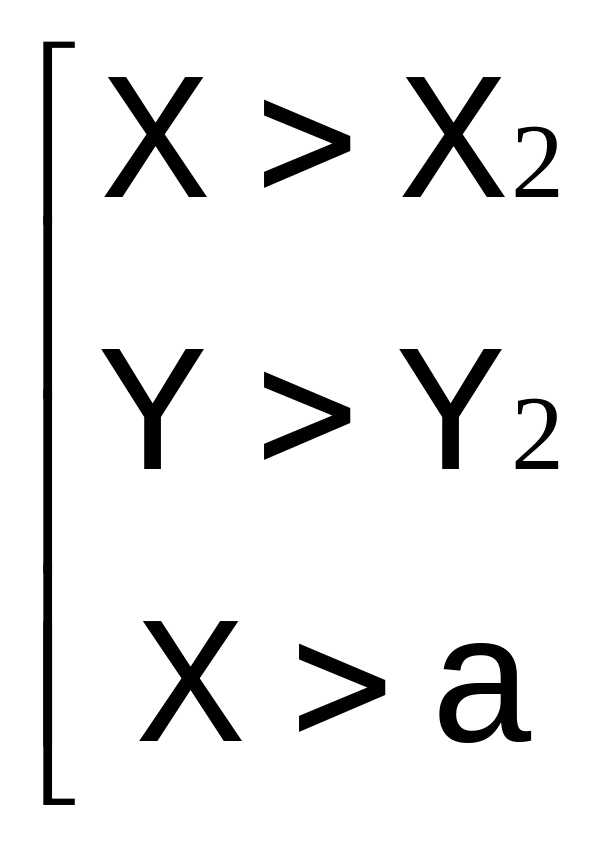(т.е. достижение края прямоугольника или конца отрезка)