2.3.2 Обратные итерации

Пусть как и пре­ж­де u₀ – про­из­воль­ный ве­к­тор; A – не­вы­ро­ж­ден­ная ма­т­ри­ца про­стой стру­к­ту­ры. Об­рат­ны­ми ите­ра­ци­я­ми ве­к­то­ра u₀ на­зы­ва­ет­ся про­цесс по­лучения по­с­ле­до­ва­тель­но­сти ве­к­то­ров

. (34)

Ины­ми сло­ва­ми, очеред­ной ве­к­тор по­лучает­ся в ре­зуль­та­те ре­ше­ния си­с­те­мы ли­ней­ных урав­не­ний с ма­т­ри­цей A и пре­ды­ду­щим ве­к­то­ров в качес­т­ве пра­вой час­ти. Об­рат­ная ите­ра­ция с ма­т­ри­цей A рав­но­силь­на пря­мой ите­ра­ции с ма­т­ри­цей A^1. Пред­по­ло­жим, что соб­ст­вен­ные значения A про­ну­ме­ро­ва­ны в по­ряд­ке убы­ва­ния. Так как соб­ст­вен­ные значения об­рат­ной ма­т­ри­цы рав­ны об­рат­ным ве­личинам соб­ст­вен­ных значений пря­мой ма­т­ри­цы, причем соб­ст­вен­ные ве­к­то­ры обе­их ма­т­риц сов­па­да­ют, то ре­зуль­тат об­рат­ной ите­ра­ции (при _k=1) мо­ж­но за­пи­сать в ви­де:

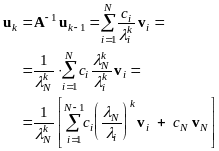
Та­ким об­ра­зом, об­рат­ная ите­ра­ция по­з­во­ля­ет оп­ре­де­лить наи­мень­шее по аб­со­лют­ной ве­личине соб­ст­вен­ное значение и со­от­вет­ст­ву­ю­щий соб­ст­вен­ный ве­к­тор.

Рас­смо­т­рим те­перь об­рат­ную ите­ра­цию со сдви­гом:

. (35)

Соб­ст­вен­ные значения ма­т­ри­цы (AE) рав­ны _i, а соб­ст­вен­ные ве­к­то­ры те же, что у ма­т­ри­цы A. Так как об­рат­ная ите­ра­ция схо­дит­ся к наи­мень­ше­му соб­ст­вен­но­му значению, то ите­ра­ция по урав­не­нию (35) по­з­во­ля­ет най­ти соб­ст­вен­ное значение, наи­бо­лее бли­з­кое к вы­бран­ной ве­личине сдви­га, т. е. то, для ко­то­ро­го раз­ность _i яв­ля­ет­ся наи­мень­шей по аб­со­лют­ной ве­личине.

Час­то об­рат­ную ите­ра­цию при­ме­ня­ют для то­го, что­бы най­ти соб­ст­вен­ные ве­к­то­ры, от­вечаю­щие уже вычис­лен­ным соб­ст­вен­ным значени­ям. В этом случае про­цесс мо­ж­но ор­га­ни­зо­вать сле­ду­ю­щим об­ра­зом:

1. Возь­мем про­из­воль­ный проб­ный ве­к­тор u₀ и вычис­лим для не­го нор­ми­ро­вочный мно­жи­тель ₁. Обоз­начим нор­ми­ро­ван­ный ве­к­тор w₀:

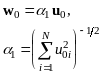
2. В качес­т­ве сдви­га ис­поль­зу­ем при­бли­жен­ную ве­личину ин­те­ре­су­ю­ще­го соб­ст­вен­но­го зна­че­ния , где  – ма­лая ве­личина, от­личная от ну­ля, по­сколь­ку сдвиг не дол­жен сов­пасть с точным соб­ст­вен­ным значени­ем. В про­тив­ном случае det(AE) ока­жет­ся ну­ле­вым, и си­с­те­му урав­не­ний (35) ре­шить не уда­ст­ся. На пра­к­ти­ке, од­на­ко, роль  иг­ра­ет не­из­бе­ж­ная вычис­ли­тель­ная по­греш­ность, и ра­вен­ст­во оп­ре­де­ли­те­ля си­с­те­мы ну­лю ма­ло­ве­ро­ят­но.

3. Най­дем ве­к­тор u₁ пу­тем ре­ше­ния си­с­те­мы (35) с w₀ в качес­т­ве пра­вой час­ти. Вычис­лим нор­ми­ро­вочный мно­жи­тель ₂ и по­лучим нор­ми­ро­ван­ный ве­к­тор w₁=₂u₁.

4. По­в­то­рим ите­ра­цию и най­дем нор­ми­ро­ван­ный ве­к­тор w₂. Срав­ним w₂ с w₁. Ес­ли раз­личия ме­ж­ду ни­ми на­хо­дят­ся в пре­де­лах же­ла­е­мой точно­с­ти, при­мем w₂ в качес­т­ве ис­ко­мо­го соб­ст­вен­но­го ве­к­то­ра. В про­тив­ном случае най­дем w₃, срав­ним его с w₂ и т. д.

2.3.3 Последовательность Штурма и метод бисекции

Пусть A – про­из­воль­ная ква­д­рат­ная ма­т­ри­ца по­ряд­ка N. Рас­смо­т­рим по­с­ле­до­ва­тель­ность ве­ду­щих под­ма­т­риц A_k (k=1,2,,N), т. е. ква­д­рат­ных бло­ков по­ряд­ка k, начина­ю­щих­ся в верх­нем ле­вом уг­лу и рас­по­ло­жен­ных на глав­ной ди­а­го­на­ли A. Ины­ми сло­ва­ми, A₁=a₁₁, а A_N сов­па­да­ет с A:

A₁=a₁₁, , , , .

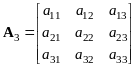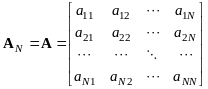Обоз­начим через P_k() ха­ра­к­те­ри­стичес­кий мно­гочлен под­ма­т­ри­цы A_k:

. (36)

Оп­ре­де­лим до­по­л­ни­тель­но мно­гочлен ну­ле­вой сте­пе­ни P₀()1. Су­ще­ст­ву­ет те­о­ре­ма^*), ко­то­рая ут­вер­жда­ет, что кор­ни со­сед­них мно­гочле­нов раз­де­ля­ют друг дру­га, т. е. ме­ж­ду дву­мя сме­ж­ны­ми кор­ня­ми мно­гочле­на P_k() на­хо­дит­ся один ко­рень мно­гочле­на P_k+1() и на­обо­рот. По­с­ле­до­ва­тель­ность мно­гочле­нов, об­ла­да­ю­щих та­ким свой­ст­вом, на­зы­ва­ют по­с­ле­до­ва­тель­но­стью Штур­ма.

Ес­ли вычис­лить значения мно­гочле­нов, об­ра­зу­ю­щих по­с­ле­до­ва­тель­ность Штур­ма, при про­из­воль­но взя­том значении пе­ре­мен­ной  и срав­нить зна­ки ве­личин P_k() (k=0,1,,N), то ока­зы­ва­ет­ся, что чис­ло пе­ре­мен зна­ка в рас­сма­т­ри­ва­е­мой чис­ло­вой по­с­ле­до­ва­тель­но­сти рав­но чис­лу соб­ст­вен­ных значений A, мень­ших, чем . До­ка­за­тель­ст­во это­го ут­вер­жде­ния (слиш­ком гро­мозд­кое, что­бы при­во­дить его здесь) мо­ж­но най­ти в кни­ге Уил­кин­со­на [Error: Reference source not found].

Обоз­начим s() чис­ло пе­ре­мен зна­ка в по­с­ле­до­ва­тель­но­сти Штур­ма, вычис­лен­ной при значении пе­ре­мен­ной . Очевид­но, раз­ность s(₂)s(₁) рав­на чис­лу соб­ст­вен­ных значений A в ин­тер­ва­ле от ₁ до ₂. Це­лочис­лен­ная функ­ция s() по ме­ре ро­с­та  мо­но­тон­но воз­рас­та­ет от 0 до N, причем ее значение уве­личива­ет­ся на 1 вся­кий раз, ко­г­да  сов­па­да­ет с очеред­ным соб­ст­вен­ным значени­ем. Та­ким об­ра­зом, вычис­ляя s(), мо­ж­но оп­ре­де­лить ко­личес­т­во соб­ст­вен­ных значений на за­дан­ном от­ре­з­ке и уточнить их по­ло­же­ние с по­мо­щью про­це­ду­ры де­ле­ния от­ре­з­ка по­по­лам (бисекции).

Для ма­т­ри­цы об­ще­го ви­да вычис­ле­ние мно­гочле­нов P_k() тре­бу­ет боль­ших вычис­ли­тель­ных за­трат, по­сколь­ку не су­ще­ст­ву­ет про­с­то­го со­от­но­ше­ния, ко­то­рое свя­зы­ва­ло бы мно­гочле­ны раз­ных сте­пе­ней k. Си­ту­а­ция значитель­но уп­ро­ща­ет­ся, ес­ли A – сим­мет­рич­ная трех­ди­а­го­наль­ная ма­т­ри­ца. В этом случае лег­ко по­лучить ре­кур­рент­ное со­от­но­ше­ние

, (37)

где d_i – ди­а­го­наль­ные, а e_i – вне­ди­а­го­наль­ные эле­мен­ты ма­т­ри­цы, т. е. , . Та­ким об­ра­зом, пре­ж­де, чем на­хо­дить соб­ст­вен­ные значения с по­мо­щью по­с­ле­до­ва­тель­но­сти Штур­ма, же­ла­тель­но при­ве­с­ти ма­т­ри­цу к трех­ди­а­го­наль­ной фор­ме, на­при­мер, пре­об­ра­зо­ва­ни­я­ми Ха­ус­хол­де­ра.

Фор­му­лы (37) весь­ма ус­тойчивы к ошиб­кам ок­руг­ле­ния. Од­на­ко их не­по­сред­ст­вен­но­му при­ме­не­нию на пра­к­ти­ке ме­ша­ет то об­сто­я­тель­ст­во, что ве­личины P_k() при k, бли­з­ких к N, час­то ока­зы­ва­ют­ся очень ма­лы­ми или очень боль­ши­ми по аб­со­лют­ной ве­личине и вы­хо­дят за гра­ни­циы ди­а­па­зо­на пред­ста­ви­мых в ма­ши­не ве­ще­ст­вен­ных чисел. В результате да­же при не очень вы­со­ких по­ряд­ках ма­т­риц воз­ни­кают пе­ре­пол­не­ния или по­я­в­ляются ма­шин­ные ну­ли.

Этой тру­д­но­сти мо­ж­но из­бе­жать, ес­ли от по­с­ле­до­ва­тель­но­сти мно­гочле­нов P_k() пе­рей­ти к по­с­ле­до­ва­тель­но­сти их от­но­ше­ний Q_k()=P_k()/P_k1(), k=1,2,,N. Так как кор­ни P_k1() на­хо­дят­ся ме­ж­ду кор­ня­ми P_k(), то оба мно­гочле­на ве­дут се­бя сход­ным об­ра­зом, и их от­но­ше­ние не дол­ж­но быть ни слиш­ком боль­шим, ни слиш­ком ма­лым (за ис­к­лючени­ем, быть мо­жет, ок­ре­ст­но­стей кор­ней P_k1(), где зна­ме­на­тель при­бли­жа­ет­ся к ну­лю). Ве­личина s() рав­на ко­личес­т­ву от­ри­ца­тель­ных значений сре­ди Q_k(), по­сколь­ку вся­кое из­ме­не­ние зна­ка в по­с­ле­до­ва­тель­но­сти Штур­ма оз­начает, что при со­от­вет­ст­ву­ю­щем k зна­ки P_k() и P_k1() про­ти­во­по­ло­ж­ны.

Для вычисления Q_k() можно воспользоваться рекуррентным соотношением

. (38)

Ес­ли в зна­ме­на­те­ле вы­ра­же­ния (38) ока­жет­ся рав­ным ну­лю, его мо­ж­но за­ме­нить не­ко­то­рой от­личной от ну­ля ма­лой ве­личиной. Как сле­ду­ет из при­ве­ден­но­го в [Error: Reference source not found] ана­ли­за оши­бок, по­доб­ная за­ме­на пра­к­тичес­ки не ухуд­ша­ет точно­с­ти оп­ре­де­ле­ния соб­ст­вен­ных значений.

Про­це­ду­ра ре­ше­ния час­тичной про­б­ле­мы соб­ст­вен­ных значений ме­то­дом де­ле­ния от­ре­з­ка по­по­лам, ос­но­ван­ная на вычис­ле­ниях функ­ции s() с при­ме­не­ни­ем со­от­но­ше­ния (38), со­дер­жит­ся в фай­ле EIGEN.PAS под на­зва­ни­ем Bisect.

2.3.4 QR-алгоритм для частичной проблемы собственных значений

Опи­сан­ные в раз­де­ле 2.2.2 QR- или QL-ал­го­рит­мы со сдви­гом мо­ж­но ис­поль­зо­вать для ре­ше­ния не толь­ко по­л­ной, но и час­тичной про­б­ле­мы соб­ст­вен­ных значений. Один шаг ал­го­рит­ма при­во­дит к оп­ре­де­ле­нию наи­мень­ше­го (с учетом вы­бран­но­го сдви­га) соб­ст­вен­но­го значения. Мно­го­крат­ное по­в­то­ре­ние та­ких ша­гов с по­с­ле­до­ва­тель­ным по­ни­же­ни­ем по­ряд­ка ма­т­ри­цы по­з­во­ля­ет най­ти m ни­ж­них соб­ст­вен­ных значений.

По­сколь­ку в случае час­тичной про­б­ле­мы соб­ст­вен­ных значений ди­а­го­на­ли­за­ция ма­т­ри­цы не до­во­дит­ся до кон­ца, соб­ст­вен­ные ве­к­то­ры в том же вычис­ли­тель­ном про­цес­се по­лучить не уда­ет­ся. Их на­хо­дят по­с­ле, при­ме­няя, на­при­мер, ме­тод об­рат­ной ите­ра­ции.

В обычном QR-ал­го­рит­ме при раз­ло­же­нии ис­ход­ной ма­т­ри­цы на про­из­ве­де­ние ор­то­го­наль­ной и тре­у­голь­ной при­ме­ня­ет­ся последовательность N1 вращений Гивенса (см. уравнение (26)), причем построение мат­ри­цы каждого элементарного поворота тре­бу­­ет из­влечения двух ква­д­рат­ных кор­ней, т. е. 2(N1) корней на одну итерацию. Ес­ли соб­ст­вен­ные ве­к­то­ры не оп­ре­де­ля­ют­ся, ока­зы­ва­ет­ся воз­мо­ж­ным по­стро­ить бо­лее эко­ном­ную схе­му вычис­ле­ний, об­хо­дя­щу­ю­ся без из­влечения ква­д­рат­ных кор­ней и тре­бу­ю­щую мень­ше­го чис­ла ариф­ме­тичес­ких опе­ра­ций. При этом ве­личина сдви­га по­лучает­ся по фор­му­ле Нью­то­на. Под­роб­но­сти мож­но най­ти в [Error: Reference source not found] и [Error: Reference source not found]. Ва­ри­ант ал­го­рит­ма без опе­ра­ций ква­д­рат­но­го кор­ня по­лучил на­зва­ние ра­ци­о­наль­но­го QR-ал­го­рит­ма (про­це­ду­ра RatQR в фай­ле EIGEN.PAS).

⁾ В ан­г­ло­я­зычной ли­те­ра­ту­ре при­ня­ты тер­ми­ны “eigenvalue” и “eigenvector”, со­ста­в­лен­ные из за­им­ст­во­ван­но­го не­мец­ко­го сло­ва “eigen” («соб­ст­вен­ный») и ан­г­лий­ских слов “value” и “vector” («зна­че­ние» и «век­тор», со­от­вет­ст­вен­но).

*⁾ Теорема Коши о разделении корней (доказательство см., например, в [Error: Reference source not found])

1. В. В. Воеводин, Ю. А. Кузнецов. Матрицы и вычисления. М.: Наука, 1984.

2. Г. Корн, Т. Корн. Справочник по математике для научных работников и инженеров. М.: Наука, 1974.

3. Дж. Х. Уилкинсон. Алгебраическая проблема собственных значений. М.: Наука, 1970.

4. Б. Парлетт. Симметричная проблема собственных значений. Численные методы. М.: Мир, 1983.

5. Дж. Уилкинсон, К. Райнш. Справочник алгоритмов на языке АЛГОЛ. Линейная алгебра. М.: Машиностроение, 1976.

14