2.2.3 Приведение симметричной матрицы к трехдиагональной форме с помощью преобразований Хаусхолдера.

В свя­зи с из­ло­жен­ны­ми вы­ше пре­и­му­ще­ст­ва­ми QL- или QR-ал­го­рит­мов для сим­мет­ричных трех­ди­а­го­наль­ных ма­т­риц, их обычно при­ме­ня­ют по­с­ле то­го, как ис­ход­ная ма­т­ри­ца тем или иным спо­со­бом при­ве­де­на к трех­ди­а­го­наль­ной фор­ме. Од­ним из наи­бо­лее эф­фе­к­тив­ных спо­со­бов та­ко­го при­ве­де­ния яв­ля­ет­ся ис­поль­зо­ва­ние пре­об­ра­зо­ва­ний Ха­ус­хол­де­ра (8).

На i-м ша­ге ал­го­рит­ма вы­пол­ня­ет­ся пре­об­ра­зо­ва­ние по­до­бия с по­мо­щью ор­то­го­наль­ной ма­т­ри­цы P_i, име­ю­щей блочную стру­к­ту­ру:

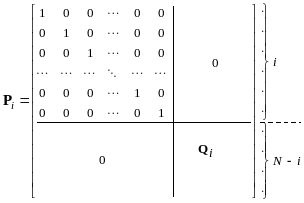, (28)

где Q_i=E2v_i·v_i (E – еди­ничная ма­т­ри­ца по­ряд­ка Ni; v_i – нор­ми­ро­ван­ный ве­к­тор той же раз­мер­но­сти). По­с­ле i1 ша­гов ис­ход­ная ма­т­ри­ца при­об­ре­та­ет вид

где зве­з­дочка­ми обоз­начены не­ну­ле­вые эле­мен­ты. Пре­об­ра­зо­ва­ние по­до­бия с по­мо­щью P_i не из­ме­ня­ет верх­ний ле­вый блок по­ряд­ка i, уже при­ве­ден­ный к трех­ди­а­го­наль­ной фор­ме. На i-м ша­ге дол­ж­ны быть ис­к­лючены все эле­мен­ты кро­ме пер­во­го в от­мечен­ных пун­к­ти­ром сим­мет­рично рас­по­ло­жен­ных стро­ке и столб­це не­ди­а­го­наль­ных бло­ков. Ус­ло­вия об­ра­ще­ния в нуль Ni1 эле­мен­тов вме­сте с ус­ло­ви­ем нор­ми­ров­ки да­ют Ni урав­не­ний, по­л­но­стью оп­ре­де­ля­ю­щих ве­к­тор v_i. Особенности практической организации вычислений изложены в [Error: Reference source not found].

Все­го для при­ве­де­ния ма­т­ри­цы к трех­ди­а­го­наль­но­му ви­ду по­тре­бу­ет­ся N2 пре­об­ра­зо­ва­ний.

По­лучение трех­ди­а­го­наль­ной ма­т­ри­цы ме­то­дом Ха­ус­хол­де­ра с по­с­ле­ду­ю­щей ее ди­а­го­на­ли­за­ци­ей с по­мо­щью QL-ал­го­рит­ма (как пра­ви­ло, с не­яв­ным сдви­гом) яв­ля­ет­ся наи­бо­лее эко­но­мичным из из­ве­ст­ных в на­сто­я­щее вре­мя ме­то­дов ре­ше­ния по­л­ной про­б­ле­мы соб­ст­вен­ных значений для плот­ных сим­мет­ричных ма­т­риц. Для лен­точных ма­т­риц эта схе­ма не яв­ля­ет­ся оп­ти­маль­ной, по­сколь­ку пре­об­ра­зо­ва­ния Ха­ус­хол­де­ра рас­ши­ря­ют лен­ту до по­л­ной ма­т­ри­цы. В этом случае бо­лее эф­фе­к­ти­вен дру­гой ал­го­ритм при­ве­де­ния к трех­ди­а­го­наль­ной фор­ме, ос­но­ван­ный на спе­ци­аль­ным об­ра­зом по­до­б­ран­ной по­с­ле­до­ва­тель­но­сти пре­об­ра­зо­ва­ний Ги­вен­са (пло­ских вра­ще­ний). Хо­тя в об­щем случае вра­ще­ние Ги­вен­са тре­бу­ет боль­ших за­трат по срав­не­нию с пре­об­ра­зо­ва­ни­ем от­ра­же­ния, для до­с­та­точно уз­кой лен­ты ко­личес­т­во пре­об­ра­зо­ва­ний со­кра­ща­ет­ся, и в ито­ге до­с­ти­га­ет­ся вы­иг­рыш в объ­е­ме вычис­ле­ний.

2.3 Методы решения частичной проблемы собственных значений

2.3.1 Прямые итерации

Пусть u₀ – про­из­воль­ный ве­к­тор, A – ма­т­ри­ца про­стой стру­к­ту­ры. По­стро­им по­с­ле­до­ва­тель­ность ве­к­то­ров

u_k=_kAu_k1, k=1,2,, (29)

где _k – не­ко­то­рые не­ну­ле­вые чис­ла. Этот про­цесс на­зы­ва­ет­ся пря­мы­ми ите­ра­ци­я­ми ве­к­то­ра u₀.

Пред­по­ло­жим, что соб­ст­вен­ные значения A про­ну­ме­ро­ва­ны в по­ряд­ке убы­ва­ния их аб­со­лют­ной ве­личины:

|₁||₂||_N|,

и пусть v₁, v₂, , v_N – со­от­вет­ст­ву­ю­щие соб­ст­вен­ные ве­к­то­ры. Пред­по­ло­же­ние о про­стой стру­к­ту­ре A оз­начает, что все v_i ли­ней­но не­за­ви­си­мы и мо­гут слу­жить ба­зи­сом про­стран­с­т­ва, т. е. лю­бой N-мер­ный ве­к­тор мо­ж­но пред­ста­вить в ви­де ли­ней­ной ком­би­на­ции соб­ст­вен­ных век­то­ров. В час­т­но­сти,

, (30)

где c_i – не­ко­то­рые (не­из­ве­ст­ные нам) ко­эф­фи­ци­ен­ты.

Пусть по­ка все мно­жи­те­ли _k=1. Рас­смо­т­рим ре­зуль­тат дей­ст­вия A на ве­к­тор u₀:

,

,



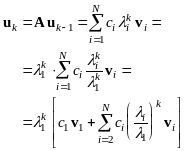
Ес­ли ₁ – наи­боль­шее соб­ст­вен­ное значение, то, очевид­но,

 при  . (31)

Рас­сма­т­ри­вая пре­дель­ное значение от­но­ше­ния двух по­с­ле­до­ва­тель­ных ре­зуль­та­тов пря­мой ите­ра­ции, мо­ж­но по­лучить наи­боль­шее соб­ст­вен­ное значение ма­т­ри­цы A:

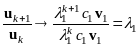. (32)

При этом u_k стре­мит­ся (с точно­стью до чис­ло­во­го мно­жи­те­ля) к со­от­вет­ст­ву­ю­ще­му соб­ст­вен­но­му ве­к­то­ру v₁.

В случае пра­к­тичес­ко­го осу­ще­ст­в­ле­ния пря­мой ите­ра­ции не­об­хо­ди­мо учиты­вать, что эле­мен­ты ве­к­то­ра u бу­дут не­ог­ра­ничен­но воз­рас­тать (или убы­вать) из-за мно­го­крат­но­го ум­но­же­ния на ве­личину ₁. Что­бы из­бе­жать это­го не­же­ла­тель­но­го эф­фе­к­та, сле­ду­ет на ка­ж­дой ите­ра­ции нор­ми­ро­вать ре­зуль­тат, вы­би­рая со­от­вет­ст­ву­ю­щим об­ра­зом мно­жи­тель _k.

Су­ще­ст­ву­ет мо­ди­фи­ци­ро­ван­ный ва­ри­ант пря­мой ите­ра­ции

, (33)

на­зы­ва­е­мый пря­мой ите­ра­ци­ей со сдви­гом. Ите­ра­ция по урав­не­нию (33) при­во­дит к ум­но­же­нию ка­ж­до­го сла­га­е­мо­го в раз­ло­же­нии (30) на ве­личину (_i_k1) вме­сто _i в случае ите­ра­ции без сдви­га. Вы­би­рая сдвиг над­ле­жа­щим об­ра­зом, мо­ж­но вли­ять на ско­рость схо­ди­мо­сти ите­ра­ций, а так­же по­лучить дру­гие соб­ст­вен­ные значения и со­от­вет­ст­ву­ю­щие ве­к­то­ры. Од­на­ко воз­мо­ж­но­сти пря­мой ите­ра­ции здесь ог­ра­ничены.