1.2.2 Преобразование подобия

Две ква­д­рат­ные ма­т­ри­цы A и на­зы­ва­ют­ся по­доб­ны­ми, ес­ли они свя­за­ны со­от­но­ше­ни­ем

, (5)

где P – не­ко­то­рая не­вы­ро­ж­ден­ная ма­т­ри­ца. Пре­об­ра­зо­ва­ние ма­т­ри­цы A, оп­ре­де­ля­е­мое урав­не­ни­ем (5), на­зы­ва­ют пре­об­ра­зо­ва­ни­ем по­до­бия, а ма­т­ри­цу P – пре­об­ра­зу­ю­щей ма­т­ри­цей. По­доб­ные ма­т­ри­цы име­ют оди­на­ко­вые оп­ре­де­ли­тель и след:

(6)

(7)

1.2.3 Матрицы со специальными свойствами

Матрица A называется симметричной, если A=A, т. е. a_ij=a_ji.

Матрица A называется эрмитовой (или самосопряженной), если A^*=A, т. е. a_ij= . Для вещественных матриц свойства симметричности и эрмитовости совпадают.

Ма­т­ри­ца A на­зы­ва­ет­ся ор­то­го­наль­ной, ес­ли A=A^1, т. е. AA=AA=E. Как из­ве­ст­но, вся­кая ма­т­ри­ца за­да­ет не­ко­то­рое пре­об­ра­зо­ва­ние в со­от­вет­ст­ву­ю­щем ли­ней­ном про­стран­с­т­ве. Пре­об­ра­зо­ва­ния, от­вечаю­щие ор­то­го­наль­ным ма­т­ри­цам, на­зы­ва­ют­ся ор­то­го­наль­ны­ми. При ор­то­го­наль­ных пре­об­ра­зо­ва­ни­ях не изменяются скалярные произведения, а сле­до­ва­тель­но, сохраняются дли­ны ве­к­то­ров (рас­сто­я­ния ме­ж­ду точка­ми про­стран­с­т­ва) и уг­лы ме­ж­ду ве­к­то­ра­ми. В час­т­но­сти, ор­то­го­наль­ные ве­к­то­ры ос­та­ют­ся та­ко­вы­ми и по­с­ле пре­об­ра­зо­ва­ния (вероятно, этим объ­я­с­ня­ет­ся тер­мин «ор­то­го­наль­ное пре­об­ра­зо­ва­ние»).

Про­стей­ши­ми ор­то­го­наль­ны­ми пре­об­ра­зо­ва­ни­я­ми на плоскости яв­ля­ют­ся по­во­рот на угол  и зер­каль­ное от­ра­же­ние от­но­си­тель­но про­из­воль­ной прямой, проходящей через начало координат. Матрицы этих пре­об­ра­зо­ва­ний имеют, соответственно, вид:

и

, (8)

где v – ве­к­тор еди­ничной дли­ны, на­пра­в­лен­ный по нор­ма­ли к пря­мой.

В бо­лее об­щем случае N-мер­но­го про­стран­с­т­ва ма­т­ри­ца вра­ще­ния в пло­с­ко­сти, оп­ре­де­ля­е­мой i-й и j-й ко­ор­ди­на­та­ми, име­ет ана­ло­гичный вид:

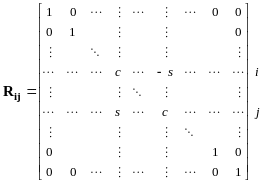, (9)

где c и s – значения cos и sin, со­от­вет­ст­вен­но. Эта ма­т­ри­ца на­зы­ва­ет­ся ма­т­ри­цей Ги­вен­са или ма­т­ри­цей эле­мен­тар­но­го по­во­ро­та. Пре­об­ра­зо­ва­ние Ги­вен­са дей­ст­ву­ет толь­ко на па­ру ко­ор­ди­нат с но­ме­ра­ми i и j; ос­таль­ные N2 ко­ор­ди­нат ос­та­ют­ся не­из­мен­ны­ми. Ма­т­ри­ца зер­каль­но­го от­ра­же­ния в про­из­воль­ной пло­с­ко­сти, про­хо­дя­щей через начало ко­ор­ди­нат в N‑мер­ном про­стран­с­т­ве, как и в случае двух из­ме­ре­ний вы­ра­жа­ет­ся урав­не­ни­ем (8), где v – ве­к­тор еди­ничной дли­ны, на­пра­в­лен­ный по нор­ма­ли к пло­с­ко­сти от­ра­же­ния. Эту мат­ри­цу (и со­от­вет­ст­ву­ю­щее пре­об­ра­зо­ва­ние) на­зы­ва­ют ма­т­ри­цей (пре­об­ра­зо­ва­ни­ем) Ха­ус­хол­де­ра.

Ма­т­ри­ца A на­зы­ва­ет­ся унитар­ной, ес­ли A^*=A^1, т. е. A^*A=AA^*=E. Для ве­ще­ст­вен­ных ма­т­риц свой­ст­ва ор­то­го­наль­но­сти и уни­тар­но­сти сов­па­да­ют.

1.3 Проблема собственных значений

1.3.1 Собственные значения и векторы

Чис­ло  на­зы­ва­ет­ся соб­ст­вен­ным значени­ем ма­т­ри­цы A, ес­ли су­ще­ст­ву­ет та­кой не­ну­ле­вой ве­к­тор v, что

Av=v. (10)

Лю­бой ве­к­тор v0, удо­в­ле­тво­ря­ю­щий урав­не­нию (10), на­зы­ва­ет­ся соб­ст­вен­ным ве­к­то­ром ма­т­ри­цы A, со­от­вет­ст­ву­ю­щим соб­ст­вен­но­му значению  ^).

Ес­ли v яв­ля­ет­ся соб­ст­вен­ным ве­к­то­ром A, то ве­к­тор v при лю­бом  так­же бу­дет соб­ст­вен­ным с тем же соб­ст­вен­ным значени­ем. Та­ким об­ра­зом, соб­ст­вен­ный ве­к­тор оп­ре­де­ля­ет­ся с точно­стью до по­сто­ян­но­го мно­жи­те­ля. На пра­к­ти­ке соб­ст­вен­ные ве­к­то­ры обычно оп­ре­де­ля­ют так, что­бы они бы­ли нор­ми­ро­ван­ны­ми, т. е. име­ли еди­ничную дли­ну:

(11)

Ес­ли ма­т­ри­ца не вы­ро­ж­де­на, то для нее су­ще­ст­ву­ет об­рат­ная ма­т­ри­ца A^1. В этом случае соб­ст­вен­ные значения A^1 рав­ны об­рат­ным ве­личинам соб­ст­вен­ных значений A, а соб­ст­вен­ные ве­к­то­ры A и A^1 сов­па­да­ют. До­ка­за­тель­ст­во не­по­сред­ст­вен­но сле­ду­ет из (10), ес­ли обе час­ти урав­не­ния ум­но­жить сле­ва на A^1.