2.3. Устойчивость линейных систем

АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

ПОНЯТИЕ УСТОЙЧИВОСТИ

Н а любую автоматическую систему всегда действуют различные внешние возмущения, которые могут нарушить ее нормальную работу [4]. В простейшем случае понятие устойчивости системы связано со способностью ее возвращаться (с определенной точностью) в состояние равновесия после исчезновения внешних сил, которые вывели ее из этого состояния. Если система неустойчива, то она не возвращается в состояние равновесия, из которого ее вывели, а либо удаляется от него, либо совершает вокруг него недопустимо большие колебания. Правильно спроектированная система должна устойчиво работать при всех внешних возмущениях.

Наглядно устойчивость равновесия представлена на рис. 2.12, где изображен шар, расположенный в некотором углублении (рис. 2.12, а), на некоторой выпуклой поверхности (рис. 2.12, б), на плоскости (рис. 2.12, в). Положение равновесия шара характеризуется точкой А₀. В случае, изображенном на рис. 2.12, а, при всяком отклонении шара от положения равновесия, например в точку A₁ он будет стремиться снова возвратиться к положению равновесия – в точку А₀ (при отсутствии сил трения) или к некоторой конечной области, окружающей положение равновесия, например в точку А₂ (при наличии сил трения). Такое положение равновесия устойчиво. Случай, изображенный на рис. 2.12, б, соответствует неустойчивому положению равновесия. Рис. 2.12, в соответствует безразличному равновесию. На рис. 2.12, г состояние равновесия устойчиво лишь до тех пор, пока отклонение не вышло за некоторую границу, определяемую, например, точкой В. Выйдя за эту границу, шар уже не вернется в точку А₀, а будет двигаться вправо от точки В либо все время удаляясь, либо до нового состояния равновесия в зависимости от формы поверхности, т. е. в конечном счете в зависимости от уравнений движения шара.

Поэтому в общем случае, рассматривая нелинейные системы, вводят понятие устойчивости «в малом», «в большом» «в целом». Система устойчива «в малом», если констатируют лишь факт наличия области устойчивости, но не определяют каким-либо образом ее границы. Систему называют устойчивой «в большом», когда определены границы области устойчивости, т. е. определены границы области, начальных отклонений, при которых система возвращается в исходное состояние, и выяснено, что реальные начальные отклонения принадлежат этой области. В том случае, когда система возвращается в исходное состояние при любых начальных отклонениях, систему называют устойчивой «в целом». Устойчивость «в целом» для определенного класса нелинейностей называют «абсолютной» устойчивостью.

Так, например, случай, изображенный на рис. 2.12, а, соответствует устойчивости «в целом», а случай, изображенный на рис. 2.12, г, может соответствовать либо устойчивости «в большом», либо устойчивости «в малом». Очевидно, что система, устойчивая «в целом», будет устойчива «в большом» и «в малом»; система, устойчивая «в большом», будет устойчива и «в малом».

На рис. 2.12, д изображено еще одно принципиально возможное для нелинейных систем состояние равновесия, которое называют полуустойчивым.

Для того чтобы дать определение устойчивости равновесия, вводят понятие о невозмущенном состоянии равновесия, соответствующем состоянию покоя в точке А₀ на рис. 2.12, а, и возмущенном состоянии, соответствующем, например, точке А₁, в которую внешняя сила привела шар и затем прекратила свое действие. Система будет устойчивой, если из возмущенного состояния она перейдет в некоторую заданную область, окружающую невозмущенное состояние равновесия.

В рассмотренном выше примере с шаром вопрос об устойчивости решается довольно просто. Однако следует заметить, что в общем случае далеко не всегда ясно, при каких условиях равновесное положение системы будет устойчивым.

Понятие устойчивости можно распространить и на более общий случай, когда в качестве невозмущенного состояния рассматривают не положение равновесия системы, а ее движение, например движения системы по некоторой наперед заданной траектории.

Допустим, что заданное движение системы при отсутствии возмущений должно определяться некоторым законом изменения независимых координат Y₁(t), Y₂(t), …, Y_п(t). По аналогии со случаем равновесия положения, заданное движение называют невозмущенным движением. Внешние возмущения, действующие на систему, вызовут отклонение действительного движения системы от заданного. Действительное движение системы называют возмущенным движением. Пусть действительное движение системы определяется независимыми координатами y₁(t), y₂(t), …, y_п(t). В общем случае y₁(t) Y₁(t), y₂(t) Y₂(t), …, y_n(t) Y_n(t).

Заданное невозмущенное движение будет устойчивым, если после приложения внешних сил (возмущений), которые затем снимают, возмущенное движение по истечении некоторого времени войдет в заданную область | y_i(t) – Y_i(t) | ε_i, где ε_i = const – заданные величины, i = 1,2,..., п.

Чтобы проиллюстрировать сказанное, предположим, что невозмущенное движение происходит по траектории А, а возмущенное движение происходит по траектории Б (рис. 2.13, а. Возьмем на этих траекториях две произвольные точки N^A и N^Б, отвечающие одному и тому же моменту времени t. При устойчивом движении траектория Б должна быть близка к траектории А.

Рис. 2.13

Следует заметить, однако, что близость траекторий А и Б является необходимым условием устойчивости движения, но недостаточным. Действительно, расстояние между точками N^A и N^Б отвечающими одному и тому же моменту времени, может возрастать не только для расходящихся, но и для близких траекторий (рис. 2.13, б).

В наиболее благоприятном случае свободная составляющая регулируемой величины, которая создается начальными условиями, с течением времени стремится к нулю. Такую систему называют устойчивой (асимптотически устойчивой).

Возможно также, что свободная составляющая стремится к некоторому конечному значению или совершает гармонические колебания, амплитуда которых стремится к некоторому конечному значению. Такие системы называют нейтральными (нейтрально устойчивыми).

Возможно, наконец, что свободная составляющая регулируемой величины неограниченно возрастает или совершает гармонические колебания с неограниченно возрастающей амплитудой. Такие системы называют неустойчивыми.

Итак, система является устойчивой, если после прекращения внешнего воздействия она по истечении некоторого времени возвращается к тому состоянию равновесия или вынужденного движения, в котором находилась до начала воздействия.

Оценка устойчивости системы есть оценка ее принципиальной способности осуществлять регулирование, поэтому с оценки устойчивости начинают исследование всякой системы.

УСЛОВИЕ УСТОЙЧИВОСТИ

Дифференциальное уравнение линейной или линеаризованной системы имеет следующий вид (2.17):

, (2.82)

где у = у(t), g = g(t) и f = f (t) — соответственно регулируемая величина, задающее воздействие и возмущение или отклонения этих величин от их базисных значений; — постоянные коэффициенты; т < п и l<n.

Для оценки устойчивости системы должна быть исследована свободная составляющая решения уравнения (2.82), т. е. необходимо решение однородного уравнения

(2.83)

при начальных условиях общего вида

, (2.84)

где — постоянные, ограниченные по абсолютной величине.

Общее решение однородного уравнения (2.83) есть сумма слагаемых, вид которых определяется значениями корней характеристического уравнения

. (2.85)

Следует заметить, что коэффициенты уравнения (2.85) и, следовательно, значения его корней зависят только от параметров системы — от свойств и параметров ее элементов, способа их соединения [5].

Отдельные слагаемые в решении уравнения (2.83) могут иметь вид (2.27)—(2.32). Если характеристическое уравнение CAУ не имеет кратных корней (что наиболее вероятно, когда корни вычисляют приближенно), то решение уравнения (2.83) будет иметь слагаемые вида

; (2.86)

. (2.87)

Слагаемое вида (2.86) соответствует вещественному корню и слагаемое вида (2.87) соответствует паре сопряженных комплексных корней , где — постоянные, и — постоянные интегрирования, которые зависят от начальных условий и всегда ограничены по абсолютной величине.

При исследовании решения уравнения (2.83), если одно его слагаемое неограниченно возрастает по абсолютной величине, то обязательно неограниченно возрастает по абсолютной величине и вся сумма в целом (независимо от наличия членов с разными знаками).

Очевидно, что присутствие одного положительного вещественного корня достаточно для того, чтобы соответствующее ему слагаемое в решении уравнения (2.83) неограниченно возрастало по абсолютной величине. При наличии одной пары сопряженных комплексных корней с положительной вещественной частью в решении уравнения (2.83) оказывается гармоническое слагаемое с неограниченно возрастающей амплитудой. В обоих случаях система оказывается неустойчивой.

Таким образом, для устойчивости (асимптотической устойчивости) линейной системы необходимо и достаточно, чтобы все корни ее характеристического уравнения имели отрицательную вещественную часть. При наличии хотя бы одного корня с положительной вещественной частью система неустойчива.

Среди корней характеристического уравнения может быть корень, равный нулю или пара чисто мнимых корней . Если при этом вещественные части всех остальных корней отрицательные, то решение уравнения (2.83) будет иметь соответственно постоянное слагаемое или гармоническое слагаемое с постоянной амплитудой . В этих случаях система нейтральная.

Сформулированное выше условие устойчивости справедливо как для линейных, так и для линеаризованных систем (теоремы Ляпунова): по корням характеристического уравнения системы, элементы которой описываются линеаризованными уравнениями, действительно можно судить о ее устойчивости. Однако в случае нулевых или чисто мнимых корней характеристического уравнения линеаризованной системы вопрос об устойчивости может быть решен только на основании исследования ее нелинейных уравнений.

Корни алгебраического уравнения, как и всякие комплексные числа, удобно представлять в виде точек на комплексной плоскости. Для устойчивости линейной системы необходимо и достаточно, чтобы все корни характеристического уравнения лежали слева от мнимой оси комплексной плоскости (рис. 2.14, а), или все корни были «левыми».

Е сли хотя бы один вещественный корень или одна пара сопряженных комплексных корней находится справа от мнимой оси, то система неустойчива (рис. 2.14, б).

М нимая ось является, следовательно, границей устойчивости. Говорят, что система находится на границе устойчивости, если нулевой корень (рис. 2.14, в) или пара чисто мнимых корней (рис. 2.14, г), а остальные корни «левые». В первом случае, который имеет место при , уравнения (2.82) и (2.83) определяют только скорость изменения искомой переменной у, а сама эта переменная у будет зависеть еще и от своего начального значения. Во втором случае в системе возникают незатухающие гармонические с постоянной амплитудой.

КРИТЕРИИ УСТОЙЧИВОСТИ

На практике для упрощения вычислений устойчивость систем определяют с помощью некоторых критериев без вычисления корней характеристического уравнения. Критерий устойчивости — это математическая формулировка условий, которым удовлетворяют коэффициенты характеристического уравнения устойчивой системы. Критерии устойчивости эквивалентны по содержанию сформулированному выше условию устойчивости [5].

Системы первого и второго порядка устойчивы, если все коэффициенты характеристического уравнения больше нуля. Для систем более высокого порядка положительность коэффициентов характеристического уравнения является необходимым, но недостаточным условием устойчивости. Если все коэффициенты уравнения положительные, то все его вещественные корни отрицательные, но среди комплексных корней могут быть и корни с положительной вещественной частью. Если хотя бы один из коэффициента отрицателен, то система заведомо неустойчива. При равенстве нулю коэффициента система находится на границе устойчивости. При равенстве нулю какого-либо другого коэффициента система либо на границе устойчивости, либо неустойчивая.

В любом случае необходимым и достаточным условием устойчивости является условие, чтобы все корни лежали в левой полуплоскости. Выяснить соблюдение этого условия без решения характеристического уравнения (т. е. без нахождения корней) позволяют критерии устойчивости. Они делятся на алгебраические и частотные. К алгебраическим относят критерий Гурвица, к частотным — критерий Михайлова и критерий Найквиста.

Критерий Гурвица удобен для исследования устойчивости систем третьего и четвертого порядков, когда известны параметры системы. Кроме того, он позволяет получить аналитическое выражение (выражения) для границ области возможных значений какого-либо параметра системы, при которых сохраняется устойчивость.

При использовании критерия Михайлова, кроме определения устойчивости, легко установить, в каких пределах можно изменять тот или иной параметр системы.

По критериям Гурвица и Михайлова можно судить об устойчивости системы как в замкнутом, так и в разомкнутом состоянии для исследования устойчивости системы рассматривают ее характеристическое уравнение.

Критерии Найквиста наиболее широко используют по следующим причинам:

1. Устойчивость замкнутой системы исследуют по частотной передаточной функции ее разомкнутой цепи, а эта функция чаще всего состоит из простых сомножителей. Коэффициентами являются реальные параметры системы, что позволяет выбирать их из условия устойчивости.

2. Для исследования устойчивости можно использовать экспериментальные частотные характеристики наиболее сложных элементов системы (объект регулирования, исполнительный элемент), что повышает точность полученных результатов.

3. Исследовать устойчивость можно по логарифмическим частотным характеристикам, построение которых не требует трудоемких расчетов.

4. Удобно определять запас устойчивости.

АЛГЕБРАИЧЕСКИЙ КРИТЕРИЙ ГУРВИЦА

Алгебраический критерий Гурвица исследует устойчивость замкнутой системы по характеристическому уравнению (знаменателю передаточной функции замкнутой системы)

; . (2.88)

Составим главный определитель Гурвица:

. (2.89)

Матрица коэффициентов, содержащая n-строк и n-столбцов, составляется следующим образом: по диагонали от левого верхнего до правого нижнего углов записываются все коэффициенты по порядку от a₁, до а_n; каждая строка дополняется коэффициентами с возрастающими индексами слева направо так, чтобы чередовались строки с нечетными и четными индексами. Отсутствие коэффициента, а также, если его индекс меньше нуля или больше n, заменялся нулем в матрице.

Система будет устойчива (т. е. все корни имеют отрицательную вещественную часть), если главный определитель и все диагональные миноры и т. д. будут больше нуля.

;

. (2.90)

Необходимое и достаточное условие наличия у характеристического уравнения пары чисто мнимых корней, при этом система будет на границе колебательной устойчивости:

. (2.91)

Из последнего условия ( ) можно найти предельное значение одного из коэффициентов, и, коэффициента усиления системы, которые называются критическими.

Можно не вычислять определители, а пользоваться таблицей:

Порядок САУ	Условие сходимости по Гурвицу
1
2
3
4
5

Пример. Составить условие устойчивости одноконтурной системы, состоящей из трех апериодических звеньев. Передаточная функция разомкнутой системы

, (2.92)

где k — передаточный коэффициент разомкнутой системы; - постоянные времени апереодических звеньев. Характеристическое уравнение замкнутой системы:

или , (2.93)

где ; ; ; .

Характеристическое уравнение третьей степени все его коэффициенты положительные. Для устойчивости еще должно удовлетворяться неравенство . Оно может быть приведено к следующему виду: , откуда следует . Обозначим и . Тогда условие устойчивости имеет вид . Устойчивость системы зависит не от абсолютных значении постоянных времени, а лишь от соотношения между ними.

КРИТЕРИЙ УСТОЙЧИВОСТИ МИХАЙЛОВА

Частотный критерий устойчивости Михайлова позволяет судить об устойчивости замкнутой или разомкнутой системы по годографу характеристического вектора (по годографу Михайлова). Характеристический вектор P(j) получается из характеристического полинома

(2.94)

путем подставки p = j :

, (2.95)

где X() – вещественная часть, функция четных степеней ; Y() – мнимая часть, функция нечетных степеней :

(2.96)

(2.97)

Годограф Михайлова есть кривая, которую описывает вектор P(j) на комплексной плоскости при изменении  от 0 до . Годограф начинается при  = 0 на вещественной оси в точке и при уходит в бесконечность в соответствующем квадранте. Угол поворота характеристического вектора определяется следующим выражением:

, (2.98)

где п — степень характеристического полинома (порядок характеристического уравнения);

l — число корней характеристического полинома с положительной вещественной частью.

С ледовательно, для устойчивости замкнутой системы п-го порядка необходимо и достаточно, чтобы при изменении частоты от 0 до годограф Михайлова начинался на положительной вещественной полуоси и обошел в положительном направлении (против часовой стрелки) последовательно п квадрантов, нигде не обращаясь в нуль.

На рис. 2.15 показаны годографы Михайлова устойчивых систем первого—пятого порядков с равным значением коэффициента . При четном п годограф уходит в бесконечность вдоль оси Х и при нечетном п — вдоль оси Y.

Если система находится на границе устойчивости, то годограф Михайлова проходит через начало координат так, что после небольшой его деформации около начала координат критерий удовлетворяется.

Г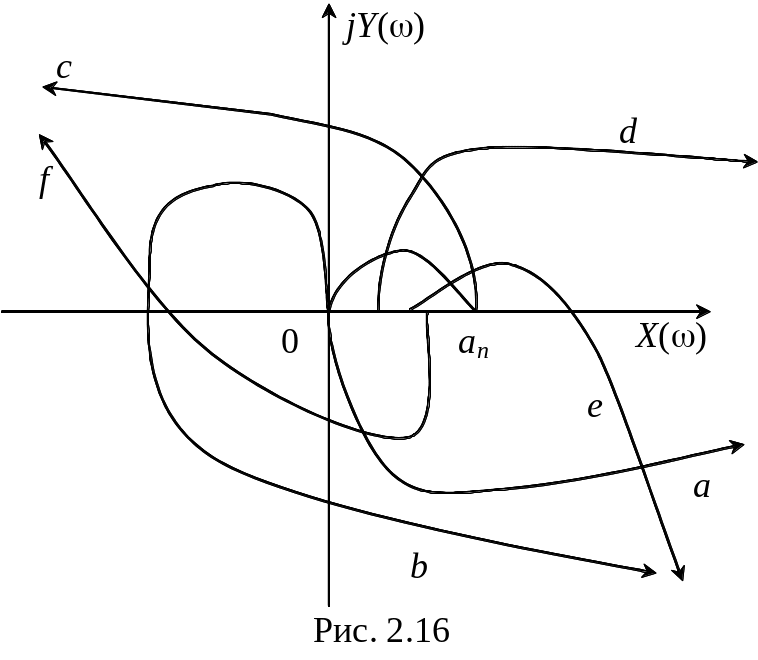 одографы Михайлова системы четвертого порядка, находящейся на границе устойчивости, показаны на рис. 2.16, а и б. В первом случае характеристический полином имеет пару чисто мнимых корней (колебательная граница устойчивости) и во втором — нулевой корень (апериодическая граница устойчивости).

У неустойчивых систем годографы Михайлова имеют разнообразную форму. На рис. 2.16 с,d,e,f показаны годографы неустойчивых систем четвертого порядка. Их характеристический полином имеет положительный вещественный корень (кривая c), два положительных вещественных корня (кривая d), два комплексных сопряженных корня с положительной вещественной частью (кривая e), два чисто мнимых корня и положительный вещественный корень (кривая f).

Иногда удобнее пользоваться другой формулировкой критерия Михайлова [5]: для устойчивости замкнутой системы необходимо и достаточно, чтобы корни мнимой (полином Y) и вещественной (полином X) частей ее характеристического вектора были положительными вещественными и чередовались, т. е. удовлетворялись неравенства:

(2.99)

где — корни полинома Y; — корни полинома X. Удобнее вычислять квадраты корней полиномов Х и Y и определять устойчивость по выполнению неравенств:

(2.100)

КРИТЕРИЙ УСТОЙЧИВОСТИ НАЙКВИСТА

Частотный критерий Найквиста дает возможность определить устойчивость замкнутой системы по амплитудно-фазовой частотной характеристике ее разомкнутой цепи, если удовлетворяется условие (в частности, С = 0). Для удовлетворения этого условия степень т числителя передаточной функции W разомкнутой системы не должна быть выше степени n ее знаменателя, что выполняется для любых реальных систем.

Предварительно должна быть определена устойчивость исследуемой системы в разомкнутом состоянии. Для неустойчивой разомкнутой системы нужно выяснить, какое число корней ее характеристического полинома имеет положительные вещественные части.

В одноконтурной системе, составленной из последовательно соединенных звеньев, корни характеристических полиномов Q_i(p) этих звеньев являются одновременно корнями характеристического полинома разомкнутой системы. Определение в этом случае не вызывает затруднений. Если какое-либо звено одноконтурной системы охвачено обратной связью, то нужно определить корни характеристического полинома этого замкнутого контура. Они войдут в число корней характеристического полинома разомкнутой системы.

Различают три случая применения критерия Найквиста.

1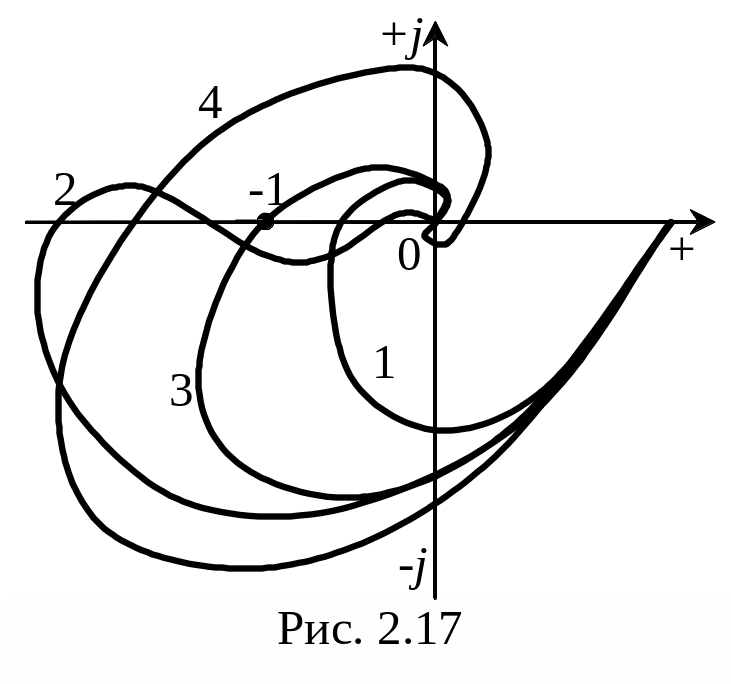 . Разомкнутая система устойчивая. В этом случае для устойчивости замкнутой системы необходимо и достаточно, чтобы амплитудно-фазовая частотная характеристика разомкнутой системы при изменении  от 0 до не охватывала точку с координатами [-1, j0].

На рис. 2.17 изображены возможные ситуации. При АФЧХ, показанной кривой 1, замкнутая система абсолютно устойчива, т. е. она остается устойчива и при уменьшении передаточного коэффициента разомкнутой цени. Если АФЧХ является кривая 2, то замкнутая система условно устойчива. Она остается устойчивой только при значении k, лежащем в некоторых пределах. Кри­вая 3 проходит через критическую точку с координатами [—1, j0). Это означает, что замкнутая система находится на колебательной границе устойчивости. Кривая 4 охватывает критическую точку, поэтому замкнутая система неустойчивая.

2. Разомкнутая система на границе устойчивости. Характеристический полином такой разомкнутой системы имеет нулевые или чисто мнимые корни, а у остальных корней отрицательные вещественные части. Если нулевых корней v, то АФЧХ при =0 дугой бесконечно большого радиуса перемещается от положительной вещественной полуоси на угол по часовой стрелке. Такие АФЧХ показаны на рис. 2.18 (а – v=1, замкнутая система устойчивая; б – v=2, замкнутая система на границе устойчивости).

Е сли есть пара чисто мнимых корней (в знаменателе частотной передаточной функции имеется множитель ), то АФЧХ при частоте ,- дугой бесконечно большого радиуса перемещается на угол —180° (по часовой стрелке).

В обоих случаях для устойчивости замкнутой системы необходимо и достаточно, чтобы амплитудно-фазовая частотная характеристика разомкнутой системы при изменении  от 0 до , дополненная на участке разрыва дугой бесконечно большого радиуса, не охватывала точку с координатами [-1, j0].

АФЧХ разомкнутой системы, характеристический полином которой имеет чисто мнимые корни, показана на рис. 2.19. При замыкании эта система будет неустойчивой.

3. Разомкнутая система неустойчивая. Характеристический полином такой системы имеет l корней с положительной вещественной частью.

В этом, наиболее общем, случае критерий Найквиста формулируют так: для устойчивости замкнутой системы необходимо и достаточно, чтобы при изменении  от 0 до вектор, начало которого находится в точке с координатами [-1, j0], а коней на амплитудно-фазовой частотной характеристике разомкнутой системы, повернулся в положительном направлении (против часовой стрелки) на угол l*180°.

Х арактеристический полином разомкнутой системы, кроме корней с вещественной частью (положительной или отрицательной), может иметь нулевые и чисто мнимые корни. Тогда на участках разрыва АФЧХ должна быть дополнена дугой бесконечно большого радиуса.

При сложной форме АФЧХ разомкнутой системы удобнее применять другую формулировку критерия Найквиста, которая использует правило переходов. Переход АФЧХ при увеличении  через отрезок вещественной оси от -1 до сверху вниз считают положительным и снизу вверх отрицательным (рис. 2.20). АФЧХ может начинаться на указанном отрезке при =0 или заканчиваться при = . Тогда считается, что она совершает полперехода.

Критерий формулируют так: замкнутая система устойчива, если разность между числом положительных и отрицательных переходов амплитудно-фазовой частотной характеристики разомкнутой системы через отрезок вещественной оси от -1 до - равен . Здесь l - число корней характеристического полинома разомкнутой системы с положительной частью.

При наличии у этого полинома нулевых и чисто мнимых корней АФЧХ на участках разрыва должна быть дополнена дугой бесконечно большого радиуса.

Для применения критерия Найквиста исследуемая система может быть разомкнута в любой точке, т. е. может быть разомкнута не главная обратная связь, а одна из местных обратных связей.

ЛОГАРИФМИЧЕСКИЙ КРИТЕРИЙ УСТОЙЧИВОСТИ

Критерий Найквиста позволяет выяснить устойчивость замкнутой системы не только по АФЧХ, но также и по логарифмическим частотным характеристикам разомкнутой системы. Эту возможность используют весьма широко вследствие простоты построение таких характеристик и определения по ним запаса устойчивости [5].

Точкам перемещения годографа с отрезком действительной оси соответствуют точки, для которых

; (2.101)

П оэтому для устойчивости замкнутой системы необходимо и достаточно, чтобы при положительных значениях логарифмической амплитудно-частотной характеристики разность между числом положительных и отрицательных переходов фазочастотной характеристики через линии -180⁰ равнялись . Здесь l — число корней с положительной вещественной частью характеристического полинома разомкнутой системы, пересечение фазочастотной характеристикой линий -180° снизу вверх считается положительным переходом, а сверху вниз — отрицательным.

При система устойчива, если разность между числами положительных и отрицательных переходов ЛФЧХ равна нулю. Пусть разомкнутая система устойчива или ее характеристический полином имеет один нулевой корень (начальное значение фазочастотной характеристики ). Тогда для устойчивости замкнутой системы общее число переходов фазочастотной характеристики через линию -180° при положительных значениях амплитудно-частотной характеристики должно быть четным (в частности, равным нулю). На рис. 2.21 показаны наиболее характерные ЛФЧХ (1 – замкнутая система абсолютно устойчивая; 2 – условно устойчивая; 3 – на границе устойчивости; 4 – неустойчивая).

Для суждения об устойчивости обычно строят асимптотическую ЛАЧХ. К ней нужно сделать поправки около тех частот, которые ограничивают положительные участки и расположены достаточно близко от сопрягающих частот (особенно от сопрягающих частот, соответствующих колебательным звеньям).

П ример. Выяснить устойчивость системы, у которой разомкнутая цепь описывается передаточной функцией

(2.102)

где k=20; ; ; c.

Построим логарифмические частотные характеристики по следующим данным: 20lgk=26 дБ; сопрягающие частоты .

Характеристики показаны на рис. 2.22. На участке частот (до частоты среза ), при которых асимптотическая амплитудно-частотная характеристика положительная, фазочастотная характеристика (не пересекает линии -180°). Поэтому делаем вывод, что замкнутая система устойчивая. Однако, асимптотической ЛФЧХ, так как частота среза находится на достаточном удалении от ближайших к ней сопрягающих частот и .