Показательные неравенства

Как мы помним, показательная функция  возрастает при всех действительных значениях  , если  .  Это значит, что большему значению аргумента соответствует большее значение функции. То есть из неравенства

следует неравенство 

Аналогично, так как показательная функция убывает, если  ,  и большему значению аргумента соответствует меньшее значение функции, из  неравенства

следует неравенство 

То есть при решении простейших показательных неравенств прежде чем сравнивать выражения, стоящие в показателе степени, нужно сравнить с единицей основание степеней.

Еще раз, это важно:

если основание степени больше единицы, то при переходе к выражениям, стоящим в показателе, знак неравенства сохраняется

если основание степени больше нуля, но меньше единицы, то при переходе к выражениям, стоящим в показателе, знак неравенства меняется на противоположный.

Все показательные неравенства любого уровня сложности, в конечном итоге, сводятся к решению простейших показательных неравенств.

Рассмотрим несколько примеров.

1. Решим неравенство:

Так как основание степеней  , при переходе к выражениям, стоящим в показателе, знак неравенства меняется на противоположный:

Перенесем все влево, и приведем к общему знаменателю:

Корни числителя:

,   

Решим неравенство методом интервалов: нанесем корни числителя и знаменателя на числовую ось и расставим знаки:

Ответ:   ,   ,  

2. Решим неравенство:

Перенесем все слагаемые влево и разложим основания степеней на простые множители:

Если бы это было уравнение, мы решали бы его с помощью замены переменной. Поступим также.

Вообще, показательные неравенства делятся на те же типы, что и показательные уравнения, и решаются теми же способами.

Внимание! Если мы решаем неравенство с помошью замены переменных, то нужно решать  относительно замены до получения простейшего неравенства. Поясню  на этом примере.

Введем замену:  , 

Получим систему неравенств:

Отсюда:

То есть 

Запишем двойное неравенство в виде системы:

Вот теперь мы можем вернуться к исходной переменной:

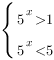
Отсюда:  ,  

Ответ: 

Показательные неравенства

Теория Учебный элемент № 1

Рассмотрим решение показательных неравенств вида , где b – некоторое рациональное число. Если a>1, то показательная функция монотонно возрастает и определена при всех х. Для возрастающей функции большему значению функции соответствует большее значение аргумента. Тогда неравенство равносильно неравенству . Если  0<a<1, то показательная функция монотонно убывает и определена при всех х. Для убывающей функции большему значению функции соответствует меньшее значение аргумента. Тогда неравенство равносильно неравенству

Рассмотрите приведенные ниже примеры решения показательных неравенств вида . 

Пример 1. Решим неравенство

Запишем неравенство в виде . Т. к. , то показательная функция возрастает. Поэтому данное неравенство равносильно неравенству . Ответ: .

Пример 2. Решим неравенство .

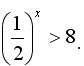Запишем неравенство в виде .

Т. к. , то показательная функция убывает. Поэтому данное неравенство равносильно неравенству . Ответ: .

Решите неравенства:

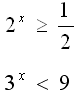
Дайте полное обоснование решения неравенств (см. примеры). Проконтролируйте правильность решения неравенств, сверив полученные ответы с ответами соседа по парте.