Міністерство освіти і науки України Вінницький національний технічний університет Методичні вказівки

до лабораторних робіт

з курсу

“Кінцеві пристрої абонентського доступу”

для студентів напрямку 6.050903 – “Телекомунікації”

Затверджено

на засіданні кафедри ТКСТБ

протокол № ___ від _______ 2014 р.

Вінниця – 2014

Лабораторна робота №1

«Дослідження QPSR-модулятора»

Мета виконання лабораторно-практичної роботи – вивчення алгоритму роботи та структурної схеми QPSR-модулятора, принципу формування кодувальної послідовності та синфазної і квадратурної компонент фазо- модульованого сигналу.

1. Теоретичні відомості

Розрізняють два типи фазової модуляції: власне фазову і відносну фазову модуляцію. При фазовій модуляції (Phase Shift Key, PSK) для передачі логічних нулів і одиниць використовують сигнали однієї і тієї ж частоти і амплітуди, але зміщені відносно один одного по фазі. Наприклад, логічний нуль передається синфазним сигналом, а логічна одиниця - сигналом, зрушеним за фазою на 180°.

Якщо зміна фази може приймати всього два значення, то говорять про двійкову фазову модуляцію (Binary Phase Shift Key, BPSK). Математично сигнал, що відповідає логічному нулю, можна представити як

а сигнал, що відповідає логічній одиниці, - як

Тоді модульований сигнал можна записати у вигляді:

,

де V(t) - керуючий сигнал, що приймає значення +1 і -1. Причому значення сигналу +1 відповідає логічному нулю, а значення сигналу -1 - логічній одиниці.

Зміна фази може мати і більше двох значень, наприклад чотири (0, 90, 180 і 270°). У цьому випадку говорять про так звану квадратурну фазову модуляцію (Quadrature Phase ShiftKey, QPSK).

Щоб зрозуміти походження цього терміна, розглянемо загальний вигляд сигналу, модульованого по фазі:

.

З урахуванням найпростіших тригонометричних співвідношень дану формулу нескладно привести до вигляду:

.

З отриманого виразу видно, що вихідний сигнал можна представити у вигляді суми двох гармонійних складових, зміщених одна відносно одної по фазі на 90°, оскільки

.

У передавачі, що виконує модуляцію, одна з цих складових є синфазною сигналу генератора, а друга знаходиться в квадратурі по відношенню до цього сигналу (звідси - квадратурна модуляція). Синфазна складова позначається як I (In Phase), а квадратурна - як Q (Quadrature).

Початковий сигнал нескладно перетворити, але попередньо зауважимо, що буде зручним, якщо надати ВЧ-сигналу початкову фазу . У цьому випадку завжди будуть наявними і синфазна і квадратурна компоненти і, більше того, для квадратурної фазової модуляції вони будуть по модулю однаковими (фази 45, 135, 225, 315 (-45) градусів).

Отже,

Якщо ввести позначення: , , то отримаємо такий вигляд сигналу:

;

.

Коефіцієнти d_і та d_q є кодувальними сигналами. Вони можуть приймати значення +1 і -1, якщо враховувати реальні значення фази . Співвідношення між зсувом фази і кодувальними сигналами наведено в табл. 1.

Таблиця 1. Співвідношення між зсувом фази і кодуючими сигналами

0° +1 +1

90° +1 -1

180° -1 -1

270° -1 +1

Фаза d_і d_q

При реалізації квадратурної фазової модуляції вхідний потік біт перетворюється в кодувальну послідовність {dk} так, що логічному нулю відповідає кодувальний біт +1, а логічній одиниці - кодувальний біт -1. Після цього кодувальний потік розділяється на парні і непарні біти. Парні біти надходять в I-канал, а непарні - в Q-канал. Причому тривалість кожного кодувального імпульсу di та dq в два рази більша тривалості початкового імпульсу dk (елементів вхідної цифрової послідовності). Нижче, рис.1, наведена часова діаграма роботи QPSK-модулятора.

Рис. 1 - Квадратурна фазова модуляція QPSK

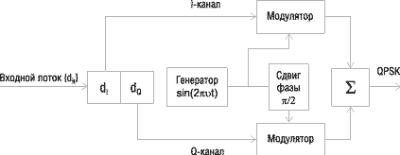
Рис. 2 - Реалізація квадратурної фазової модуляції

Кодувальні біти d_і модулюють по фазі сигнал

а біти d_q модулюють ортогональний сигнал (зміщений по фазі на 90 °), тобто

Після цього обидва сигнали додаються і утворюється модульований сигнал.

У наведеній вище схемі квадратурної фазової модуляції фаза результуючого сигналу може змінюватися тільки кожні 2T секунд. Відмінною особливістю квадратурної фазової модуляції є наявність чотирьох дискретних станів сигналу, що відповідають різним фазам. Це дозволяє закодувати в одному дискретному стані послідовність двох інформаційних біт (так званий дібіт). Дійсно, послідовність двох біт може мати лише чотири різні комбінації: 00, 01, 10 і 11. Отже, рівно в два рази підвищується і швидкість передачі даних, тобто бодова швидкість в два рази менша бітової (1 Бод = 2 біт / с).

Враховуючи, що кодувальному біту +1 відповідає логічний нуль, а кодувальному біту -1 - логічна одиниця, і, беручи до уваги відповідність між фазою сигналу і значеннями d_і та d_q, отримаємо таблицю відповідності між вхідними дібітами і фазами модульованого сигналу.

Таблиця 2. Відповідності між вхідними дібітами і фазами модульованого сигналу

Фаза сигнала d_і d_q Вхідний дібіт

сигнала di dq Входной дибит

0° +1 +1 00

90° +1 -1 01

180° -1 -1 11

270° -1 +1 10

Рис.3 - Векторна діаграма стану

Можливі дискретні стани сигналу прийнято зображати на векторній діаграмі стану або на площині сигнального сузір'я. При використанні векторної діаграми стану кожному значенню сигналу ставиться у відповідність вектор, довжина якого - це умовна амплітуда сигналу, а кут повороту вектора відносно горизонтальної осі - це фаза сигналу. Тобто векторна діаграма - це не що інше, як зображення векторів стану в полярній системі координат. Приклади діаграм стану для двійкової та квадратурної фазової модуляцій показані на рис.3.

Більш широке поширення одержав спосіб відображення різних станів сигналу на сигнальному сузір'ї. Сигнальне сузір'я - це декартова система координат, по осі абсцис якої відкладаються значення кодувального сигналу d_і (вісь I), а по осі ординат - значення кодуючого сигналу d_q (вісь Q). У разі двійкової фазової модуляції площина вироджується в пряму, вздовж якої відкладаються значення кодувального сигналу dk. В цьому випадку на сигнальному сузір'ї розташовуються всього дві точки, що відповідають значенням кодуючих бітів 1 і -1. Ці дві точки відповідають усім можливим станам сигналу. У разі QPSK-модуляції сигнальне сузір'я складається вже з чотирьох точок з координатами (1, 1), (1, -1), (-1, 1), (-1, -1). Ці чотири точки відповідають чотирьом можливим дібітам і утворюють сукупність усіх можливих станів сигналу.

Рис. 4 - Сигнальне сузір'я для BPSK-і QPSK-модуляцій

Незважаючи на уявну простоту методу фазової модуляції йому притаманні деякі недоліки, пов'язані з труднощами технічної реалізації. Один з недоліків пов'язаний з тим, що в разі квадратурної фазової модуляції при одночасній зміні символів в обох каналах модулятора (з +1, -1 на -1, +1 або з +1, +1 на -1, -1) в сигналі QPSK відбувається стрибок фази на 180°. Такі стрибки фази, що мають місце і при звичайній двофазній модуляції, викликають паразитну амплітудну модуляцію обвідної сигналу. В результаті цього при проходженні сигналу через вузькосмуговий фільтр виникають провали обвідної до нуля. Такі зміни сигналу небажані, оскільки приводять до збільшення енергії бічних смуг і перешкод в каналі зв'язку.

Для того щоб уникнути цього небажаного явища, вдаються до так званої квадратурної фазової модуляції зі зсувом (Offset QPSK, OQPSK). При такому типі модуляції формування сигналу в квадратурній схемі відбувається так само, як і в модуляторі QPSK, за винятком того, що кодувальні біти в Q-каналі мають часову затримку на тривалість одного елемента Т. Зміна фази при такому зміщенні кодувальних потоків визначається лише одним елементом послідовності, а не двома. В результаті скачки фази на 180° відсутні, оскільки кожний елемент послідовності, що поступає на вхід модулятора синфазного чи квадратурного каналу, може викликати зміну фази на 0, 90 або 270° (-90°).

Іншим, більш серйозним недоліком фазової модуляції є та обставина, що при декодуванні сигналу приймач повинен визначати абсолютне значення фази сигналу, оскільки у фазовій модуляції інформація кодується саме абсолютним значенням фази сигналу. Для цього необхідно, щоб приймач мав інформацію про «еталонний» синфазний сигнал передавача. Тоді шляхом порівняння прийнятого сигналу з еталонним можна визначати абсолютний зсув фази. Отже, необхідно якимось способом синхронізувати сигнал передавача з еталонним сигналом приймача (з цієї причини фазова модуляція отримала назву синхронної). Реалізація синхронної передачі досить складна, тому більш широке поширення набув різновид фазової модуляції, так звана відносна фазова модуляція (Differential Phase Shift Keying, DPSK). При відносній фазовій модуляції (або відносної фазової маніпуляції) кодування інформації відбувається за рахунок зсуву фази по відношенню до попереднього стану сигналу. Фактично приймач повинен вловлювати не абсолютне значення фази прийнятого сигналу, а лише зміну цієї фази. Тобто інформація кодується зміною фази. Природно, така модуляція вже не є синхронною і простіше реалізується. У всьому іншому DPSK-модуляція не відрізняється від PSK-модуляції.

Для технічної реалізації DPSK-модуляції вхідний потік інформаційних бітів спочатку перетворюється, а потім піддається звичайній фазової модуляції. Якщо необхідно, щоб скачки по фазі відбувалися при появі логічного нуля, то перетворення вихідної послідовності зводиться до наступного: при появі нуля відбувається перетворення сигналу на інверсний, а при появі одиниці сигнал не змінюється.

На рис. 5 наведена фазова обвідна QPSK-сигналу та векторні діаграми фазо-модульованого сигналу. Алгоритм побудови наступний.

Спочатку вхідний цифровий сигнал ділиться на дібіти. Важливо зазначити, що підрахунок цифрових позицій починається з нуля (парне число), потім 1, 2, 3 і т.д. Отже, для нижченаведеного цифрового сигналу парними є сигнали: 0, 1, 0, 0, 1, 0, 1, 1 – виділені жирним шрифтом, інші непарні. Нижчий графік – кодувальна послідовність, яка далі перетворена на дві послідовності d_і та d_q. Парні сигнали визначають знак d_і (+1 або -1) на інтервалі дібіта 2Т, а непарні сигнали – знак d_q (також +1 або -1) також на цьому ж інтервалі існування дібіта. Користуючись системою координат для QPSK-модуляції (див. рис. 4) і отриманими значеннями кодувальних сигналів, які визначають значення синфазної та квадратурної компонент (див. рис. 5), можна побудувати фазову обвідну та векторні діаграми для дібітів фазомодульованого сигналу.

0 0 1 1 0 1 0 0 1 0 0 1 1 1 1 0

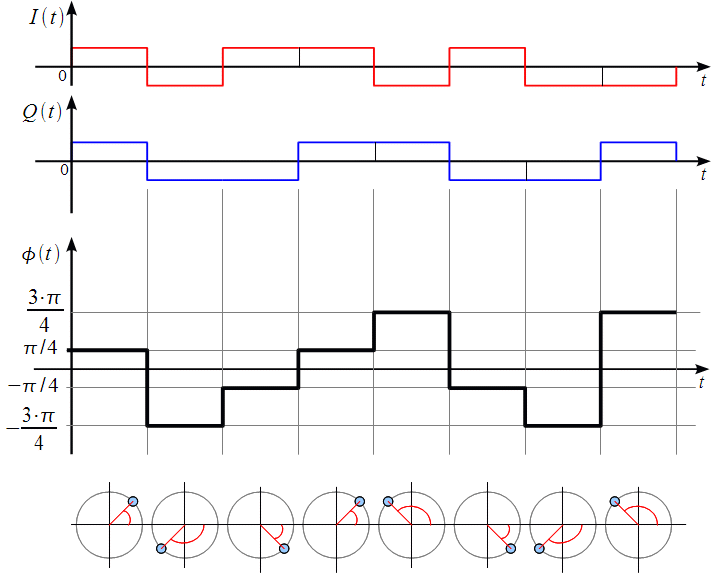
Рис. 5: Фазова обвідна QPSK сигналу