Лабораторная работа № 4

Тема: «Синтез баз нечетких знаний»

Синтез баз нечетких знаний для анализа и моделирования экономических систем в среде Matlab.

По статистическим данным в среде Matlab осуществить:

1. Проектирование систем типа Мамдани

2. Проектирование систем типа Сугэно

Провести анализ и сопоставление систем разного типа. Сформировать общетеоретические представления относительно баз знаний.

Построение нечетких систем в диалоговом режиме с помощью модуля Fuzzy.

Модуль fuzzy позволяет строит нечеткие системы двух типов - Мамдани и Сугэно. В системах типа Мамдани база знаний состоит из правил вида “Если x₁=низкий и x₂=средний, то y=высокий”.

В системах типа Сугэно база знаний состоит из правил вида “Если x₁=низкий и x₂=средний, то y=a₀+a₁x₁+a₂x₂". Таким образом, основное отличие между системами Мамдани и Сугэно заключается в разных способах задания значений выходной переменной в правилах, образующих базу знаний.

В системах типа Мамдани значения выходной переменной задаются нечеткими термами, в системах типа Сугэно - как линейная комбинация входных переменных.

Рассмотрим основные этапы проектирования систем типа Мамдани на примере создания системы нечеткого логического вывода, моделирующей зависимость , .

Проектирование системы нечеткого логического вывода будем проводить на основе графического изображения указанной зависимости.

Для построения трехмерного изображения функции в области воспользуемся программой Matlab.

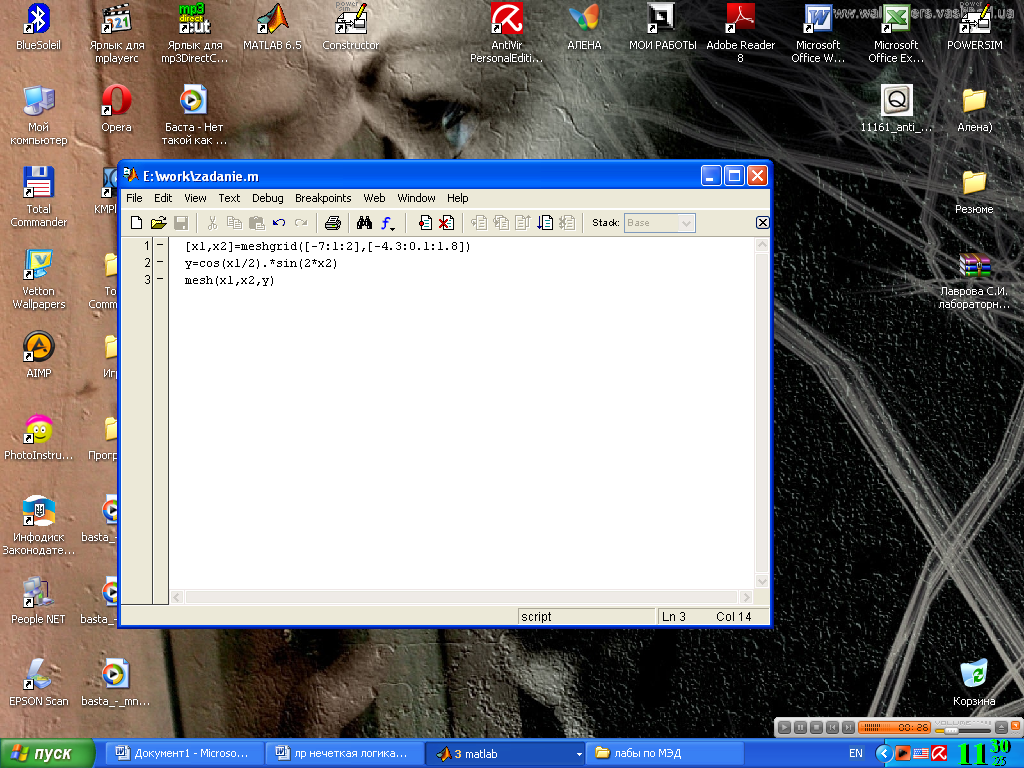
Рис 4.1. Построения трехмерного изображения функции

В результате выполнения программой Matlab заданных функций описанных на рисунке 4.1, получим графическое изображение, приведенное на рис. 4.2.

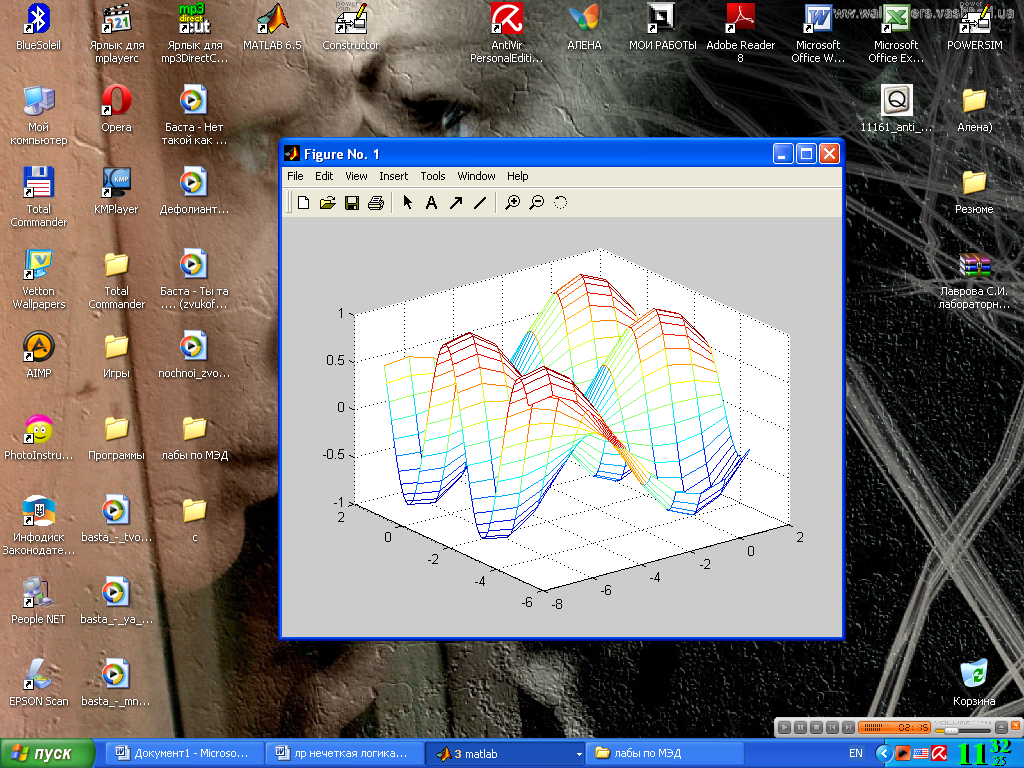
Рис. 4.2. Эталонная поверхность (графическое изображение функции ).

Проектирование системы нечеткого логического вывода, соответствующей приведенному графику, состоит в выполнении следующей последовательности шагов.

Шаг 1. Для загрузки основного fis-редактора напечатаем слова fuzzy в командной строке (рис 4.3). После этого откроется новое графическое окно, показанное на рис. 4.4.

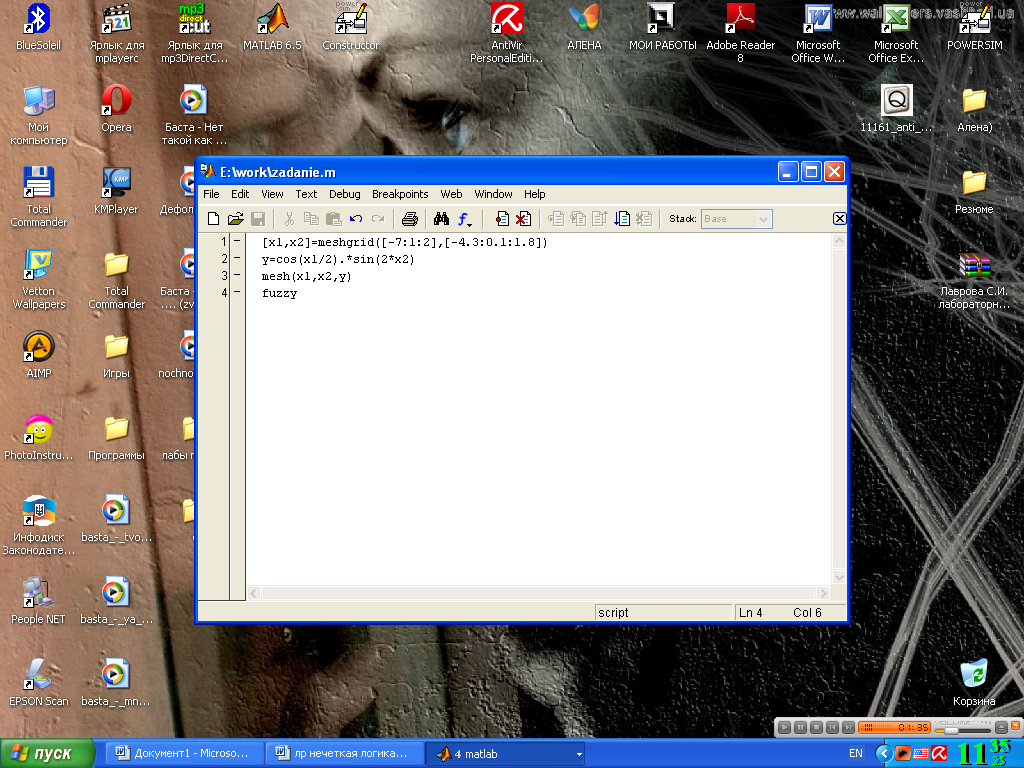
Рис. 4.3. Загрузка основного fis-редактора.

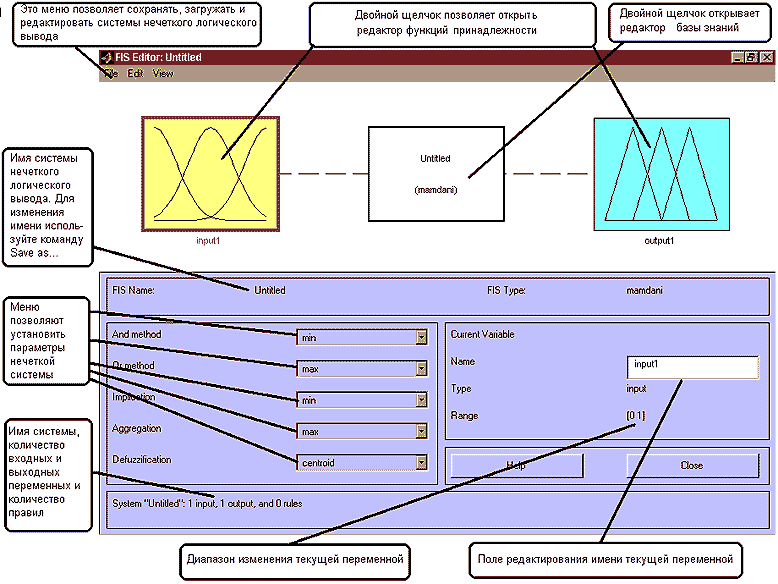
Рис. 4.4 Окно редактора FIS-Editor

Шаг 2. Добавим вторую входную переменную. Для этого в меню Edit выбираем команду Add input.

Шаг 3. Переименуем первую входную переменную. Для этого сделаем один щелчок левой кнопкой мыши на блоке input1, введем новое обозначение x1 в поле редактирования имени текущей переменной и нажмем <Enter>.

Шаг 4. Переименуем вторую входную переменную. Для этого сделаем один щелчок левой кнопкой мыши на блоке input2, введем новое обозначение x2 в поле редактирования имени текущей переменной и нажмем <Enter>.

Шаг 5. Переименуем выходную переменную. Для этого сделаем один щелчок левой кнопкой мыши на блоке output1, введем новое обозначение y в поле редактирования имени текущей переменной и нажмем <Enter>.

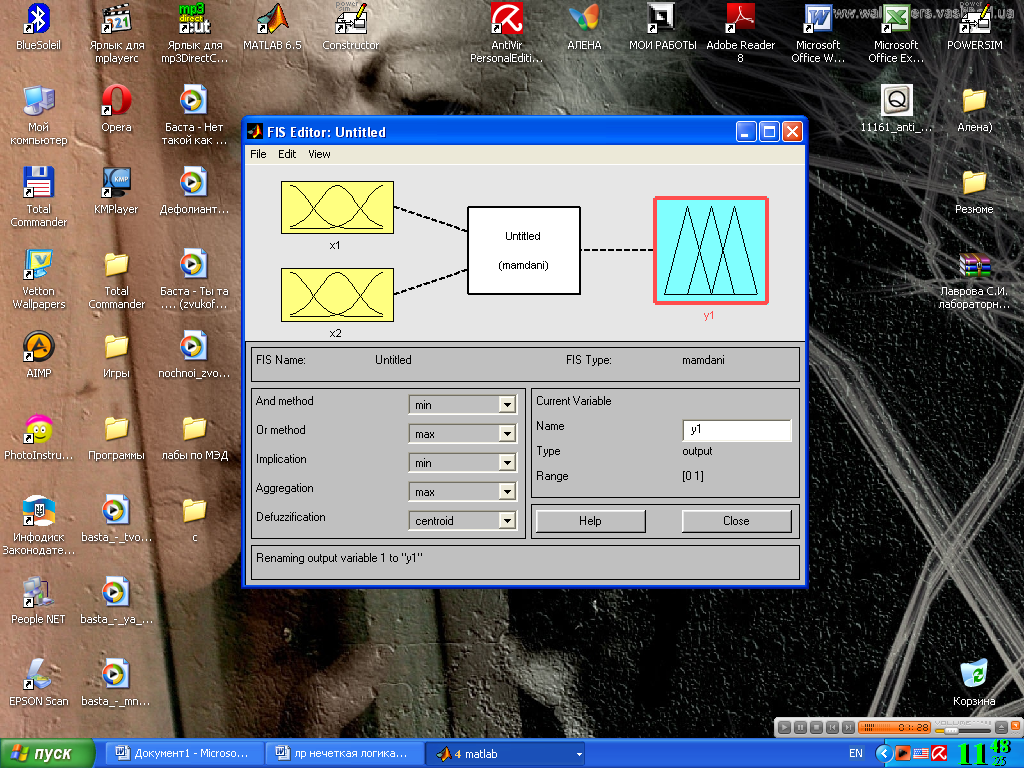
Рис. 4.5 Окно иллюстрирующее шаги 2-5

Шаг 6. Зададим имя системы. Для этого в меню File выбираем в подменю Export команду To disk и вводим имя файла, например, zadanie.

Шаг 7. Перейдем в редактор функций принадлежности. Для этого сделаем двойной щелчок левой кнопкой мыши на блоке x1.

Шаг 8. Зададим диапазон изменения переменной x1. Для этого напечатаем (-7;2) в поле Range (см. рис 4.6) и нажмем <Enter>.

Шаг 9. Зададим функции принадлежности переменной x1. Для лингвистической оценки этой переменной будем использовать 3 терма с треугольными функциями принадлежности. Для этого в меню Edit выберем команду Add MFs... В результате появиться диалоговое окно выбора типа и количества функций принадлежностей. По умолчанию это 3 терма с треугольными функциями принадлежности. Поэтому просто нажимаем <Enter>.

Шаг 10. Зададим наименования термов переменной x1. Для этого делаем один щелчок левой кнопкой мыши по графику первой функции принадлежности (см. рис 4.6). Затем вводим наименование терма, например, Низкий, в поле Name и нажмем <Enter>. Затем делаем один щелчок левой кнопкой мыши по графику второй функции принадлежности и вводим наименование терма, например, Средний, в поле Name и нажмем <Enter>. Еще раз делаем один щелчок левой кнопкой мыши по графику третьей функции принадлежности и вводим наименование терма, например, Высокий, в поле Name и нажмем <Enter>. В результате получим графическое окно, изображенное на рис 4.6.

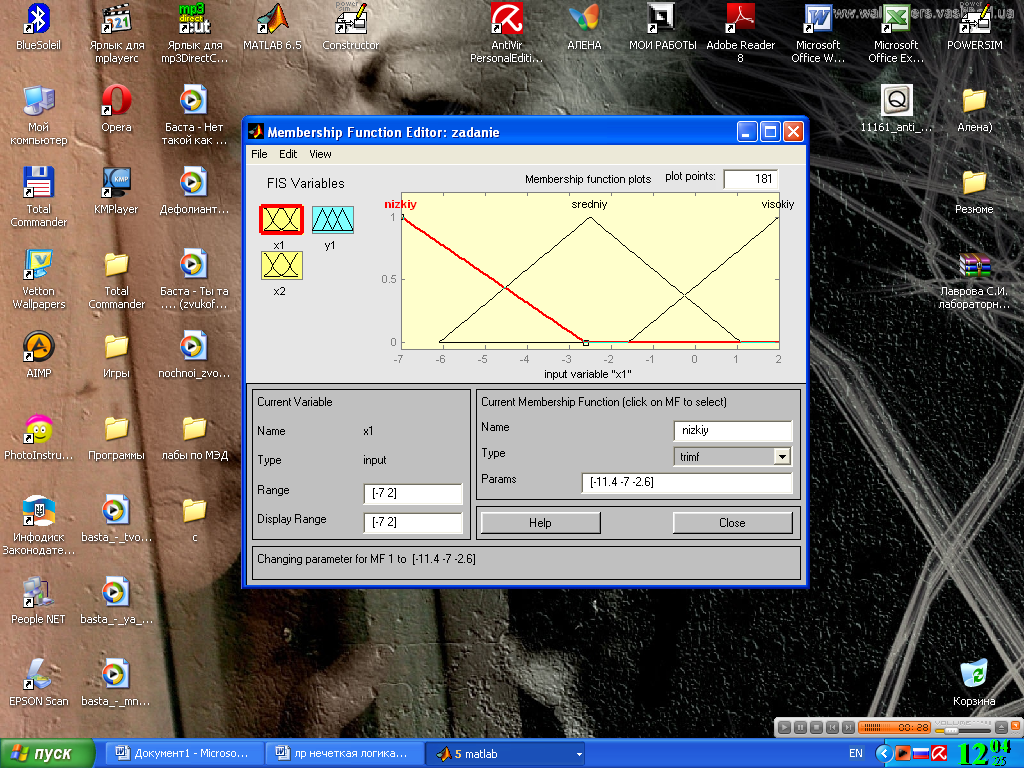
Рис. 4.6. Окно иллюстрирующее шаги 7-10

Шаг 11. Зададим функции принадлежности переменной . Для лингвистической оценки этой переменной будем использовать 5 термов с гауссовскими функциями принадлежности. Для этого активизируем переменную с помощью щелчка левой кнопки мыши на блоке . Зададим диапазон изменения переменной . Для этого напечатаем (-4.3;1.8) в поле Range (см. рис. 4.7) и нажмем <Enter>. Затем в меню Edit выберем команду Add MFs. В появившимся диалоговом окне выбираем тип функции принадлежности gaussmf в поле MF type и 5 термов в поле Number of MFs. После этого нажимаем <Enter>.

Шаг 12. По аналогии с шагом 10 зададим следующие наименования термов переменной : Низкий, Ниже среднего, Средний, Выше среднего, Высокий. В результате получим графическое окно, изображенное на рис. 4.7.

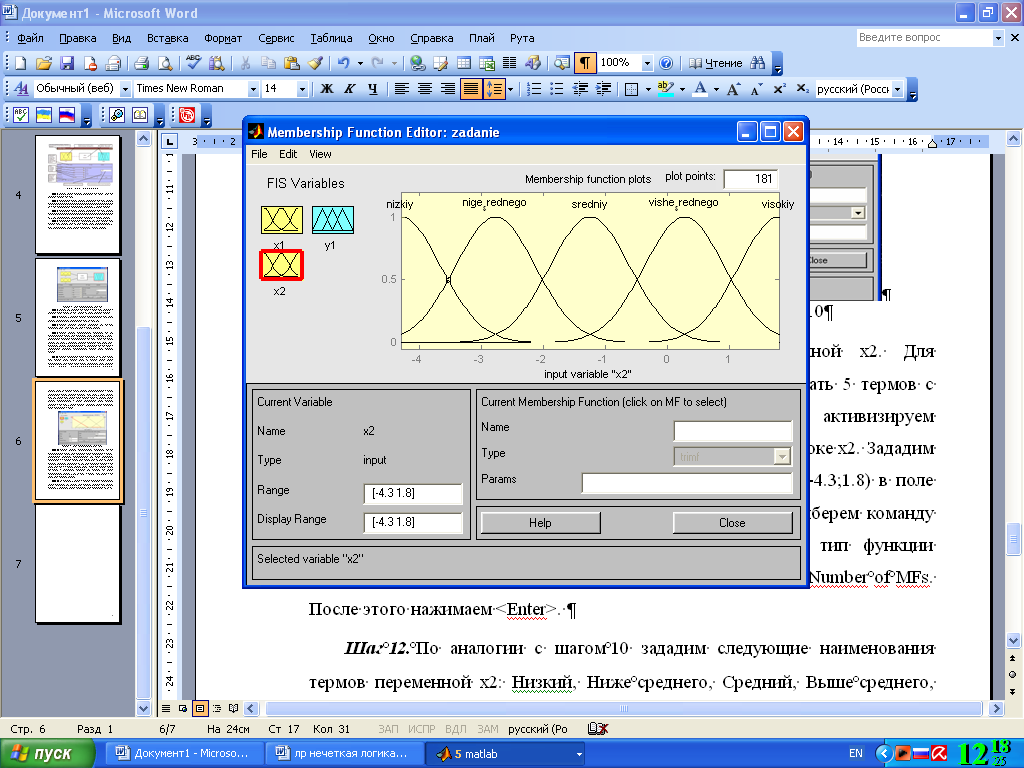
Рис. 4.7. Функции принадлежности переменной

Шаг 13. Зададим функции принадлежности переменной y. Для лингвистической оценки этой переменной будем использовать 5 термов с треугольными функциями принадлежности. Для этого активизируем переменную y с помощью щелчка левой кнопки мыши на блоке y. Зададим диапазон изменения переменной y. Для этого напечатаем (-580; 580) в поле Range (см. рис. 8) и нажмем <Enter>.Затем в меню Edit выберем команду Add MFs. В появившимся диалоговом окне выбираем 5 термов в поле Number of MFs. После этого нажимаем <Enter>.

Шаг 14. По аналогии с шагом 10 зададим следующие наименования термов переменной y: Низкий, Ниже среднего, Средний, Выше среднего, Высокий. В результате получим графическое окно, изображенное на рис. 4.8.

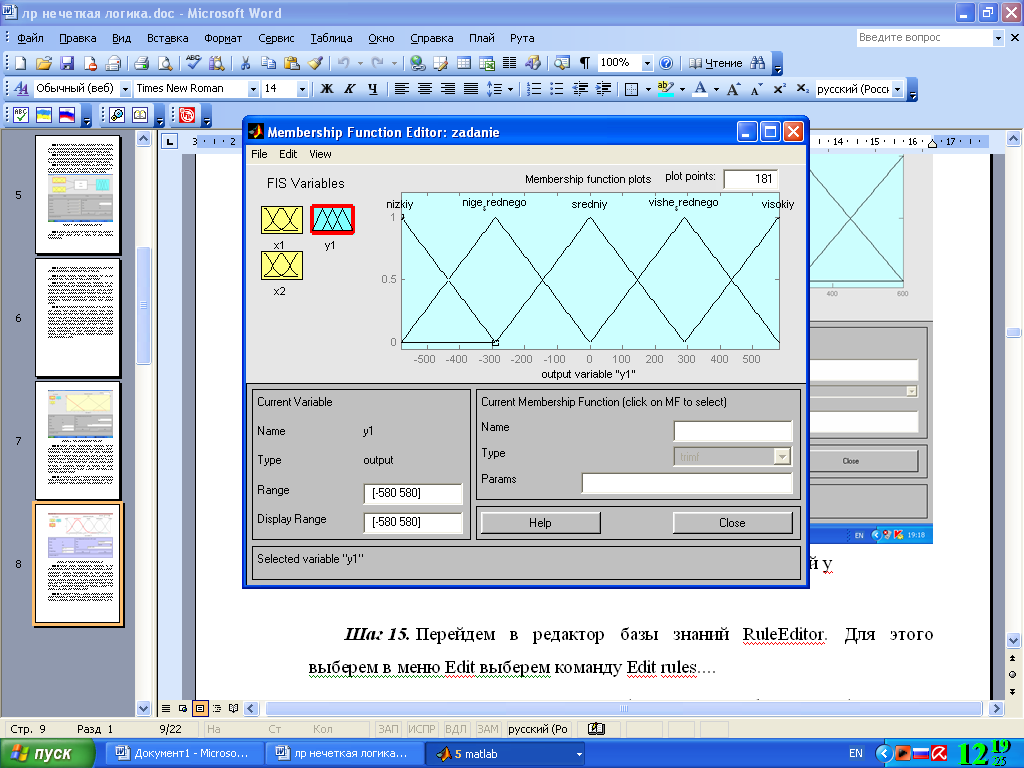
Рис. 4.8. Функции принадлежности переменной y

Шаг 15. Перейдем в редактор базы знаний RuleEditor. Для этого выберем в меню Edit выберем команду Edit rules....

Шаг 16. На основе визуального наблюдения за графиком, изображенным на рис. 2 сформулируем следующие 15 правил (рисунок 4.9).

Для ввода правила необходимо выбрать в меню соответствующую комбинацию термов и нажать кнопку Add rule. На рис. 4.9 изображено окно редактора базы знаний после ввода всех 15 правил. Число, приведенное в скобках в конце каждого правила представляет собой весовым коэффициент соответствующего правила.

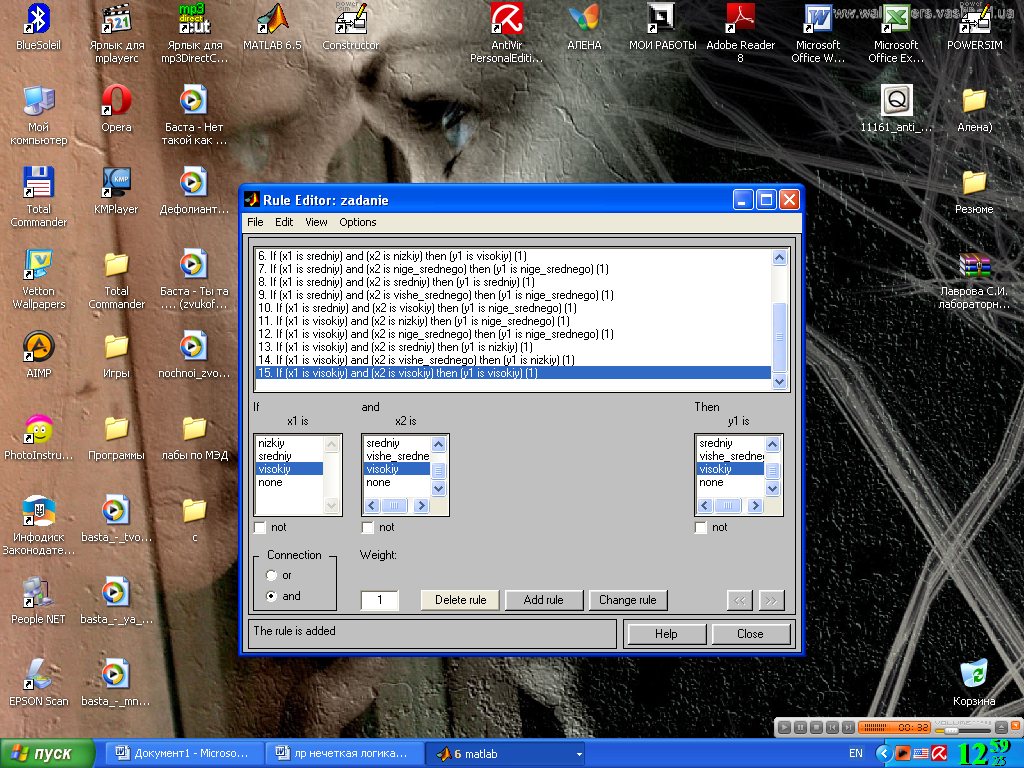
Рис. 4.9. Окно редактора базы знаний после ввода всех девяти правил

Шаг 17. Сохраним созданную систему. Для этого в меню File выбираем в подменю Export команду To disk.

На рис. 4.10 приведено окно визуализации нечеткого логического вывода. Это окно активизируется командой View rules. меню View. В поле Input указываются значения входных переменных, для которых выполняется логический вывод.

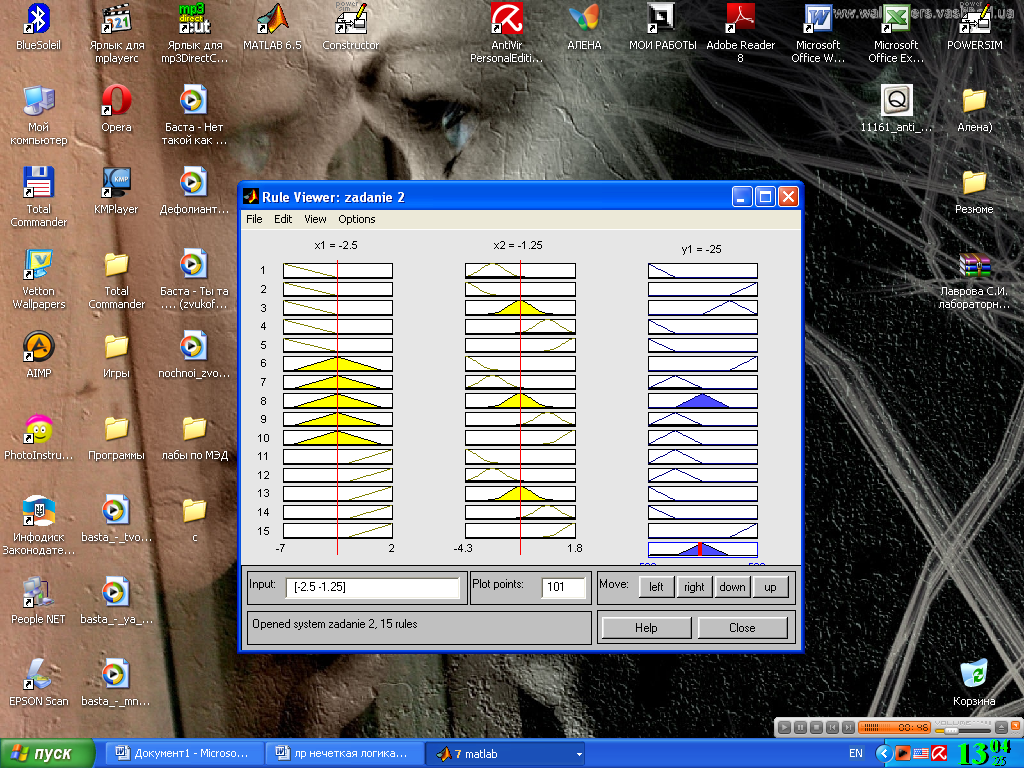
Рис. 4.10. Визуализация нечеткого логического вывода в RuleViewer

На рис. 4.11 приведена поверхность “входы-выход”, соответствующая синтезированной нечеткой системе. Для вывода этого окна необходимо использовать команду View surface... меню View.

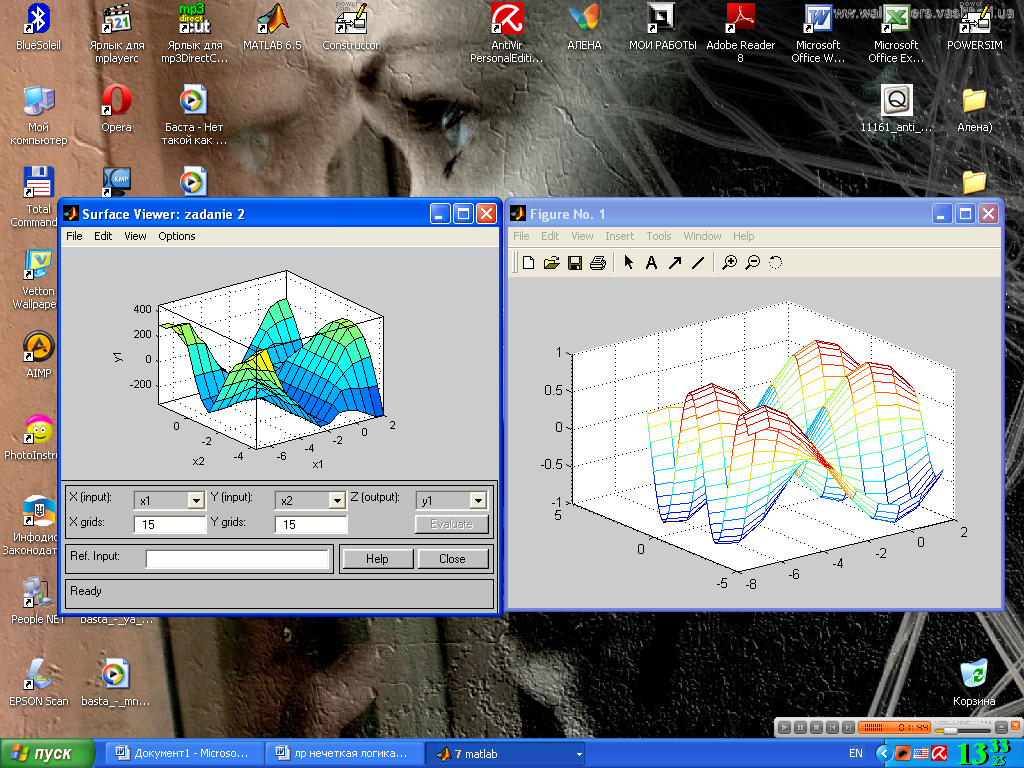
Рис. 4.11. Сравнение поверхностей

Рассмотрим основные этапы проектирования систем типа Сугэно на примере создания системы нечеткого логического вывода, моделирующей зависимость , .

Проектирование системы нечеткого логического вывода типа Сугэно состоит в выполнении следующей последовательности шагов.

Шаг 1. Для загрузки основного fis-редактора напечатаем слова fuzzy в командной строке. После этого откроется новое графическое окно, показанное на рис. 4.12.

Рис. 4.12. Загрузка основного fis-редактора

Шаг 2. Выберем тип системы. Для этого в меню File выбираем в подменю New fis… команду Sugeno.

Шаг 3. Добавим вторую входную переменную. Для этого в меню Edit выбираем команду Add input.

Шаг 4. Переименуем первую входную переменную. Для этого сделаем один щелчок левой кнопкой мыши на блоке input1, введем новое обозначение x1 в поле редактирования имени текущей переменной и нажмем <Enter>.

Шаг 5. Переименуем вторую входную переменную. Для этого сделаем один щелчок левой кнопкой мыши на блоке input2, введем новое обозначение x2 в поле редактирования имени текущей переменной и нажмем <Enter>.

Шаг 6. Переименуем выходную переменную. Для этого сделаем один щелчок левой кнопкой мыши на блоке output1, введем новое обозначение y в поле редактирования имени текущей переменной и нажмем <Enter>.

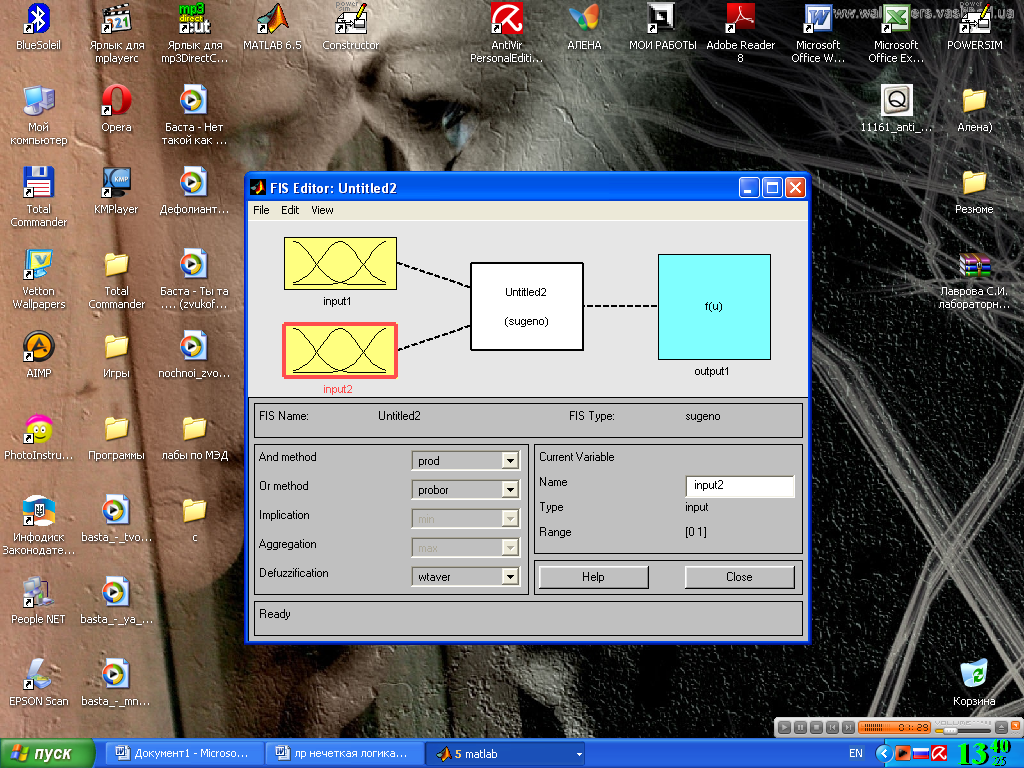
Рис. 4.13. Окно, иллюстрирующее шаги 2-6

Шаг 7. Зададим имя системы. Для этого в меню File выбираем в подменю Export команду To disk и введем имя файла, например, zadanie 1.

Шаг 8. Перейдем в редактор функций принадлежности. Для этого сделаем двойной щелчок левой кнопкой мыши на блоке x1.

Шаг 9. Зададим диапазон изменения переменной x1. Для этого напечатаем (-7; 2) в поле Range (см. рис. 4.14) и нажмем <Enter>.

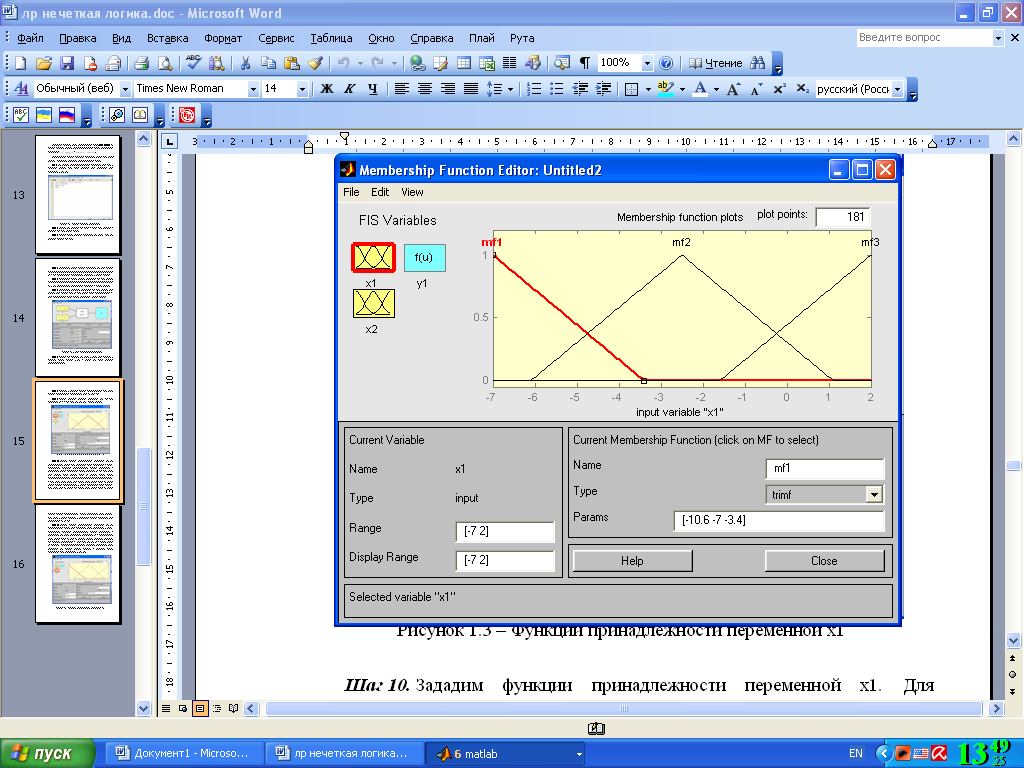
Рис. 4.14. Функции принадлежности переменной x1

Шаг 10. Зададим функции принадлежности переменной x1. Для лингвистической оценки этой переменной будем использовать, 3 терма с треугольными функциями принадлежности, которые установлены по умолчанию. Зададим наименования термов переменной x1. Для этого делаем один щелчок левой кнопкой мыши по графику первой функции принадлежности (см. рис. 4.14). Затем напечатаем наименование терма Низкий в поле Name. Затем делаем один щелчок левой кнопкой мыши по графику второй функции принадлежности и вводим наименование терма Средний в поле Name. Еще раз делаем один щелчок левой кнопкой мыши по графику третьей функции принадлежности и вводим наименование терма Высокий в поле Name и нажмем <Enter>. В результате получим графическое окно, изображенное на рис. 4.14.

Рис. 4.15. Окно, иллюстрирующее шаги 7-10

Шаг 11. Зададим функции принадлежности переменной x2. Для лингвистической оценки этой переменной будем использовать 3 терма с треугольными функциями принадлежности, которые установлены по умолчанию. Для этого активизируем переменную x2 с помощью щелчка левой кнопки мыши на блоке x2. Зададим диапазон изменения переменной x2. Для этого напечатаем (-4.3; 1.8) в поле Range (см. рис. 4) и нажмем <Enter>. По аналогии с предыдущим шагом зададим следующие наименования термов переменной x2: Низкий, Средний, Высокий. В результате получим графическое окно, изображенное на рис. 4.15.

Шаг 12. Зададим линейные зависимости между входами и выходом, приведенные в базе знаний. Для этого активизируем переменную y с помощью щелчка левой кнопки мыши на блоке y. В правом верхнем угле появилось обозначение трех функций принадлежности, каждая из которых соответствует одной линейной зависимости между входами и выходам. База знаний, необходимая для построения будет содержать 4 различных зависимости: y=255; y=4x1-x2; y=2x1+2x2+1; y=8x1+2x2+8. Поэтому добавим еще одну зависимость путем выбора команды Add Mfs… меню Edit. В появившимся диалоговом окне в поле Number of MFs выбираем 1 и нажимаем кнопку OK.

Шаг 13. Зададим наименования и параметры линейных зависимостей. Для этого делаем один щелчок левой кнопкой мыши по наименованию первой зависимости mf1. Затем печатаем наименование зависимости, например 255, в поле Name, и устанавливаем тип зависимости – константа путем выбора опции Сonstant в меню Type. После этого вводим значение параметра – 255 в поле Params.

Аналогично для второй зависимости mf2 введем наименование зависимости, например 8+8x1+2x2. Затем укажем линейный тип зависимости путем выбора опции Linear в меню Type и введем параметры зависимости 8 2 8 в поле Params. Для линейной зависимости порядок параметров следующий: первый параметр – коэффициент при первой переменной, второй – при второй и т.д., и последний параметр – свободный член зависимости.

Аналогично для третьей зависимости mf3 введем наименование зависимости, например 1+2x1+2x2, укажем линейный тип зависимости и введем параметры зависимости 2 2 1.

Для четвертой зависимости mf4 введем наименование зависимости, например 4x1-x2, укажем линейный тип зависимости и введем параметры зависимости 4 -1 0.

В результате получим графическое окно, изображенное на рис. 4.16.

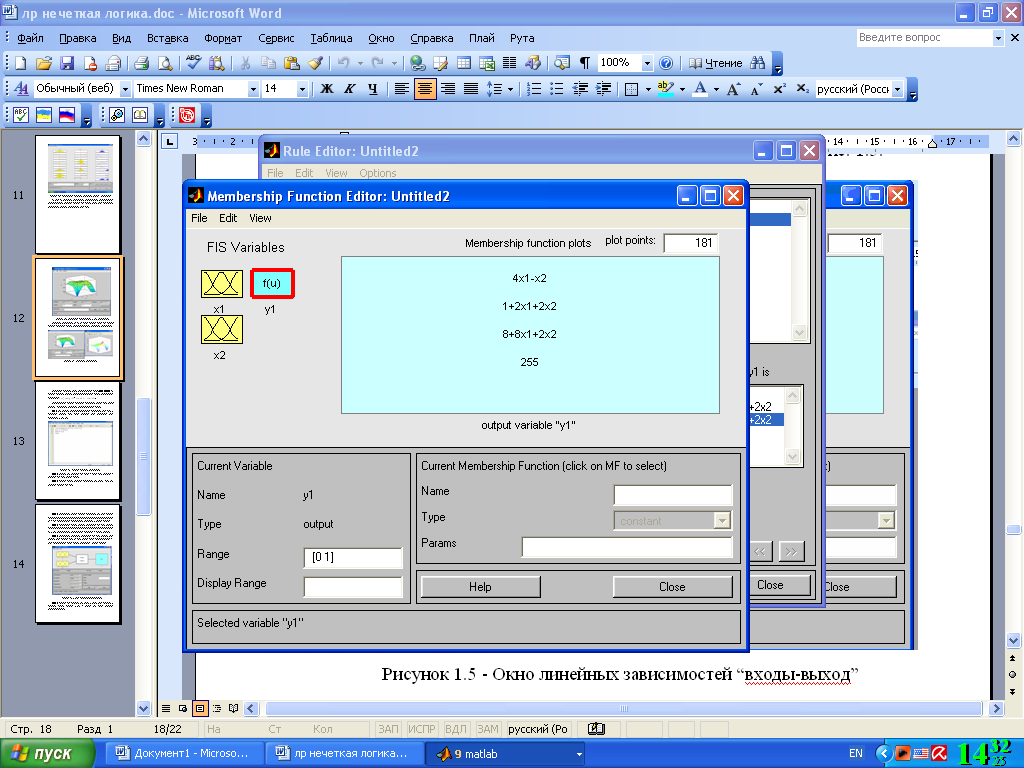
Рис. 4.16. Окно линейных зависимостей “входы-выход”

Шаг 14. Перейдем в редактор базы знаний RuleEditor. Для этого выберем в меню Edit команду Edit rules.... и введем правила базы знаний. Для ввода правила необходимо выбрать соответствующую комбинацию термов и зависимостей и нажать кнопку Add rule. На рисунке 4.17 изображено окно редактора базы знаний после ввода всех 9 правил.

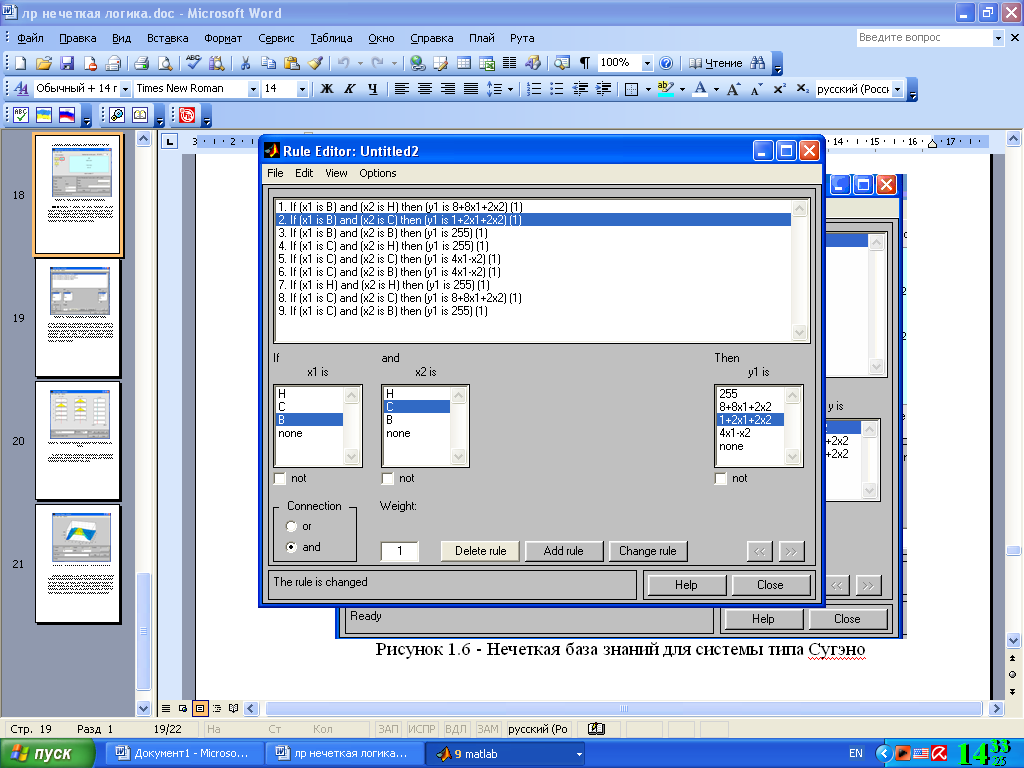
Рис. 4.17. Нечеткая база знаний для системы типа Сугэно

На рис. 4.18 приведено окно визуализации нечеткого логического вывода. Это окно активизируется командой View rules... меню View. В поле Input указываются значения входных переменных, для которых выполняется логический вывод. Как видно из этого рисунка значение выходной переменной рассчитывается как среднее взвешенное значение результатов вывода по каждому правилу.

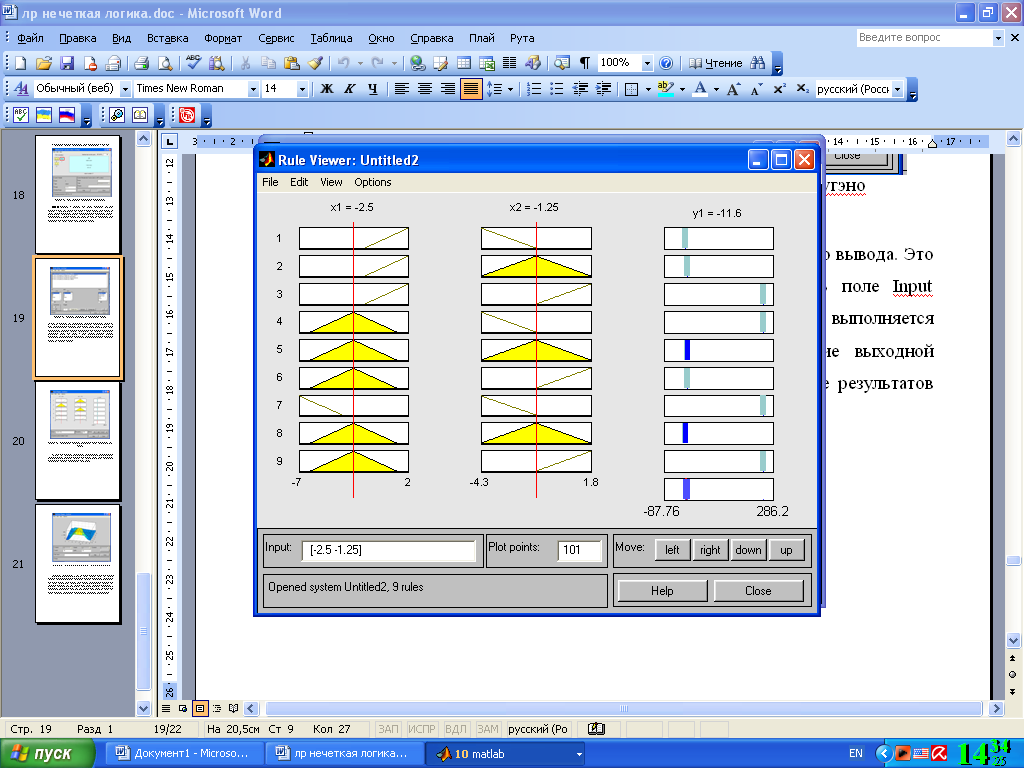
Рис. 4.18. Визуализация нечеткого логического вывода для системы типа Сугэно

На рис. 4.19 приведена поверхность “входы-выход”, соответствующая синтезированной нечеткой системе. Для вывода этого окна необходимо использовать команду View surface... меню View.

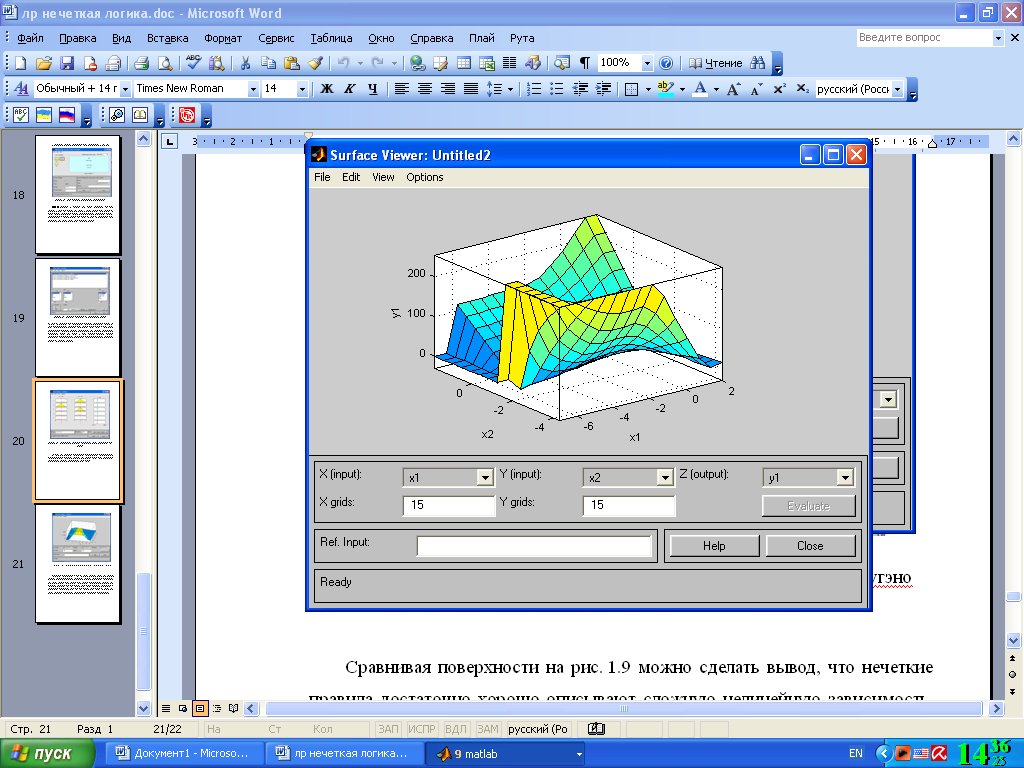
Рис. 4.19. Поверхность “входы-выход” для системы типа Сугэно

Сравнивая поверхности на рис. 4.20 можно сделать вывод, что нечеткие правила достаточно хорошо описывают сложную нелинейную зависимость. При этом, модель типа Мамдани более точная.

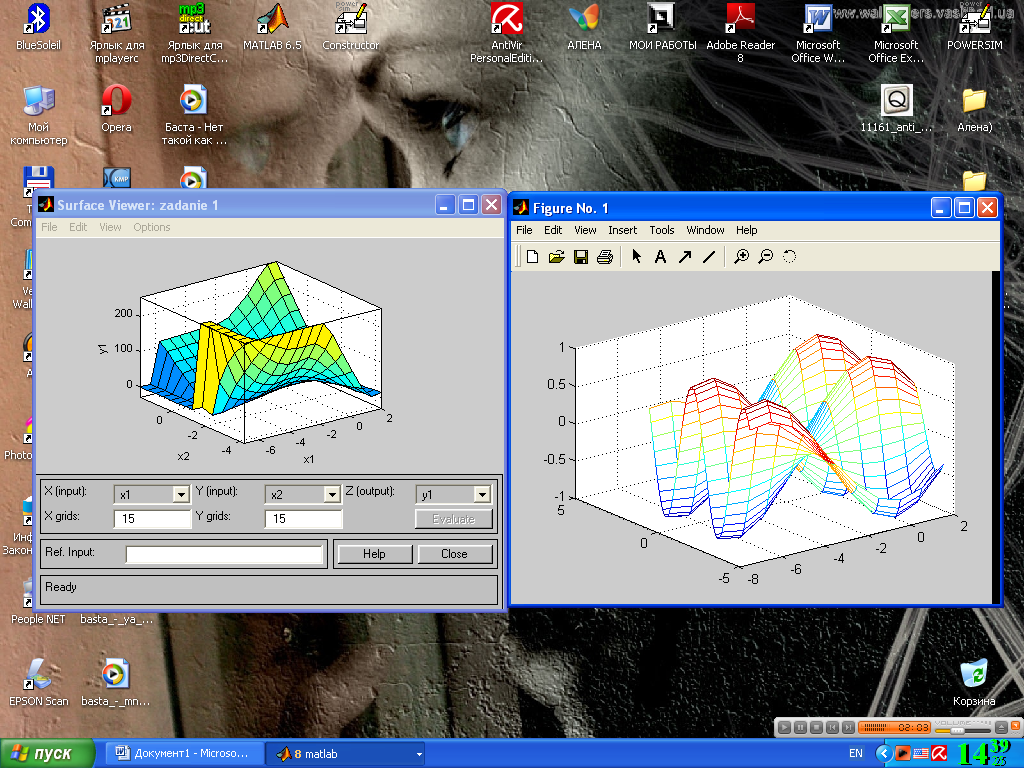
Рис. 4.20. Сравнивание поверхностей

Преимущество моделей типа Мамдани состоит в том, что правила базы знаний являются прозрачными и интуитивно понятными, тогда как для моделей типа Сугэно не всегда ясно какие линейные зависимости “входы-выход” необходимо использовать.

Задание. Для заданной по варианту функции, необходимо построить нечеткую базу знаний методами Мамдани и Сугено.

Интервал, на котором будет выполнено построение, следует выбрать исходя из наибольшей графической представительности функции на нем.

Варианты:

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

12. 

13. 

14. 

15. 

16. 

Лабораторная работа № 5

Тема: «Проектирование систем нечеткой логики»

Принятие решений в нечетких условиях по схеме Беллмана – Заде.

Принятие решения - это выбор альтернативы, которая одновременно удовлетворяет и нечетким целям, и нечетким ограничениям. В этом смысле, цели и ограничения являются симметричными относительно решения, что стирает различия между ними и позволяет представить решение как слияние нечетких целей и ограничений.

Нечеткие цели, ограничения и решения

Пусть  - множество альтернатив. Нечеткую цель будет отождествлять с нечетким множеством   в . Например, если альтернативами являются действительные числа, т.е.  , а нечеткая цель сформулирована как «x должно быть около 10», то ее можно представить нечетким множеством с такой функцией принадлежности:

(5.1)

Аналогичным образом нечеткое ограничение   определяется как некоторое нечеткое множество на универсальном множестве . Например, нечеткое ограничение «x должно быть значительно больше 8» при   можно представить нечетким множеством с такой функцией принадлежности:

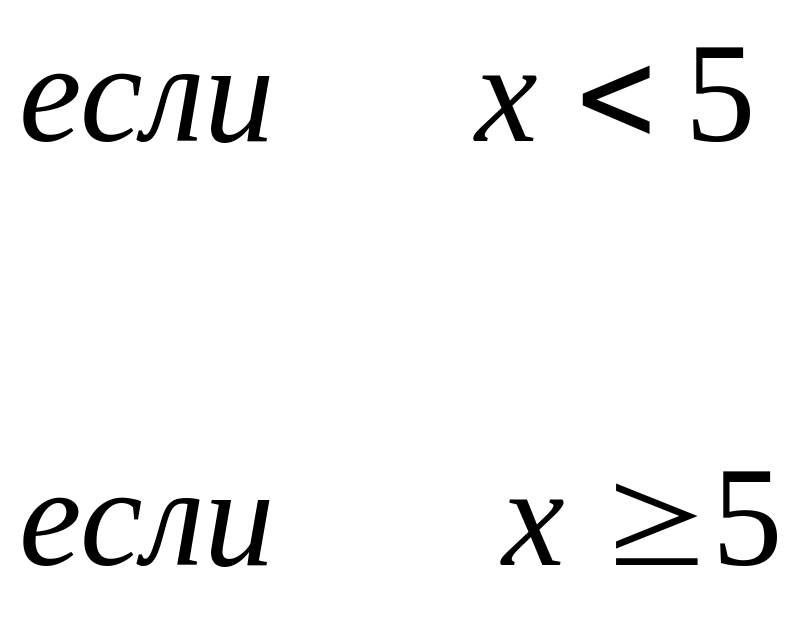(5.2)

Нечеткое решение   также определяется как нечеткое множество на универсальном множестве альтернатив . Функция принадлежности этого нечеткого множества показывает насколько хорошо решение удовлетворяет нечетким целям И ограничениям. Логической операции И, которая связывает цели и ограничения, соответствует операция пересечения нечетких множеств. Следовательно, решение - это пересечение нечеткой цели с нечетким ограничением:

(5.3)

Пример.  Нечеткая цель   и нечеткое ограничение  сформулированы так:

: «x должно быть около 10»   и    : «x должно быть значительно больше 8».

Функции принадлежности нечетких множеств   и   заданы выражениями (5.1) и (5.2). Необходимо найти нечеткое решение .

Нечеткое решение   найдем по формуле (5.3). Учитывая, что пересечению нечетких множеств соответствует операция минимума над функций принадлежности, получаем:

(5.4)

Взаимосвязь между нечеткими целью, ограничением и решением показана на рис. 5.1. Цель и ограничения конфликтуют между собой, поэтому в нечетком множестве   нет ни одного элемента со степенью принадлежности равной 1. Значит, не существует альтернативы, которая полностью удовлетворяет и цели, и ограничению. В качестве четкого решения в таких случаях обычно выбирают альтернативу с максимальной степенью принадлежности нечеткому множеству  .

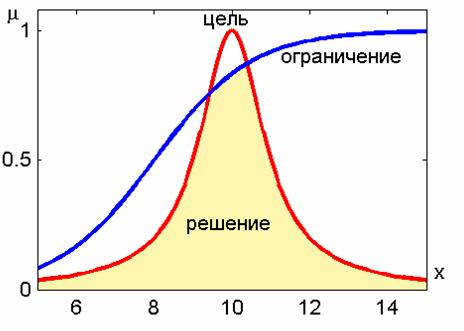
Рис. 5.1. Принятие решения по принципу Беллмана-Заде

При принятии решений по схеме Беллмана-Заде не делается никакого различия между целью и ограничениями. Всякое разделение на цель и ограничения является условным: в формуле (5.3) можно поменять местами цель с ограничением, при этом решение не изменится. В традиционной теории принятия решений подобные замены функции предпочтения на ограничение недопустимы. Однако, и здесь прослеживается некоторое скрытое сходство между целями и ограничениями. Оно становится явным при использовании метода неопределенных множителей Лагранжа и штрафных функций, когда цель и ограничения объединяются в одну функцию.

В общем случае, когда имеется n целей и m ограничений, результирующее решение по схеме Беллмана-Заде определяется пересечением всех целей и ограничений:

, (5.5)

и соответственно

. (5.6)

До сих пор предполагалось, что все цели и ограничения, входящие в , имеют одинаковую важность. Более привычная ситуация, в которой удовлетворение одним целям и (или) ограничениям, важнее чем другим. Обозначим через   - коэффициент относительной важности i-ой цели, а через   - коэффициент относительной важности j-го ограничения  . Тогда функцию принадлежности решения определяется так:

(5.7)

Чем меньше коэффициент относительной важности, тем соответствующее нечеткое множество цели или ограничения становится более размазанным, и, следовательно, его роль в принятии решения снижается. На рис. 5.2 приведены нечеткие решения при различных коэффициентах важности цели и ограничения из примера 5.1.

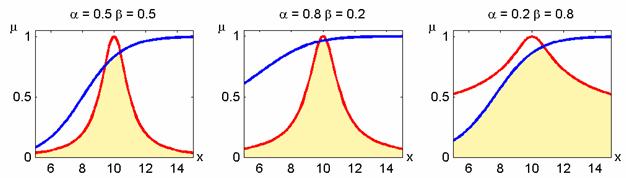
Рис. 5.2. Принятие решений при разной важности цели и ограничения

Нечеткий многокритериальный анализ вариантов.

Будем считать известными:

 - множество вариантов, которые подлежат многокритериальному анализу;

 - множество количественных и качественных критериев, которыми оцениваются варианты.

Задача многокритериального анализа состоит в упорядочивании элементов множества по критериям из множества .

Пусть   - число в диапазоне [0,1], которое характеризирует уровень оценки варианта   по критерию  : чем больше число  , тем выше оценка варианта   по критерию  , , . Тогда критерий   можно представить в виде нечеткого множества   на универсальном множестве вариантов :

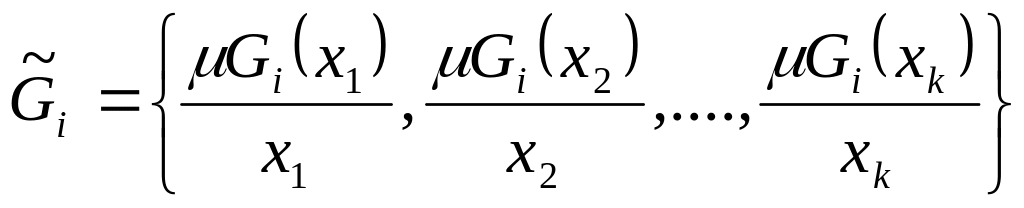, (5.8)

где   - степень принадлежности элемента   нечеткому множеству  .

Находить степени принадлежности нечеткого множества (5.8) удобно методом построения функций принадлежности на основе парных сравнений. При использовании этого метода необходимо сформировать матрицы парных сравнений вариантов по каждому критерию. Общее количество таких матриц совпадает с количеством критериев и равняется n.

Наилучшим вариантом будет тот, который одновременно лучший по всем критериям. Нечеткое решение   находится как пересечения частных критериев:

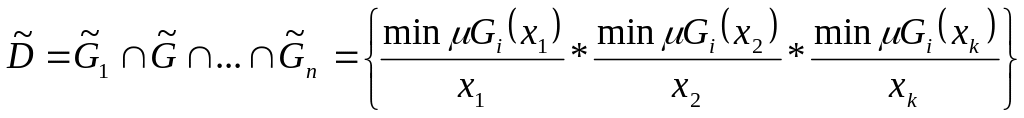, (5.9)

Согласно с полученным нечетким множеством  ‚ наилучшим вариантом следует считать тот‚ для которого степень принадлежности является наибольшей.

При неравновесных критериях формула (5.9) принимает вид:

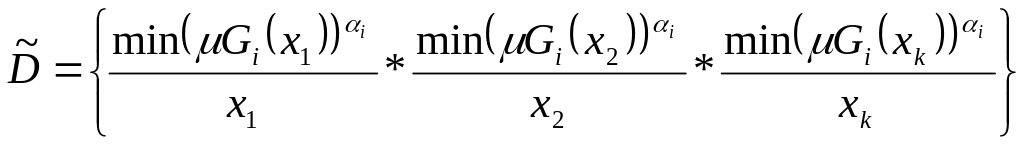, (5.10)

где  - коэффициент относительной важности критерия  ,  .

Показатель степень   в формуле (5.10) свидетельствует о концентрации нечеткого множества   в соответствии с мерой важности критерия  . Коэффициенты относительной важности критериев могут быть определены различными методами, например, с помощью парных сравнений по шкале Саати.

Нечеткий многокритериальный анализ инновационных проектов

В качестве примера принятия решений в нечетких условиях по схеме Беллмана - Заде рассмотрим сравнение технико-экономического уровня трех проектов , направленных в инновационный фонд с целью получения финансирования.

Для оценки технико-экономического уровня проектов воспользуемся такими критериями:

 - масштаб проекта;

 - новизна проекта;

 - приоритетность направления;

 - степень проработки;

 - правовая защищенность;

 - экологический уровень.

При экспертном сравнении проектов   по критериям   были получены лингвистические высказывания, показанные в таблице 5.1.

Таблица 5.1 

Парные сравнения проектов по шкале Саати

Критерий	Парные сравнения
	Отсутствие преимущества   над  Существенное преимущество   над
	Почти существенное преимущество   над  Слабое преимущество   над
	Существенное преимущество   над  Явное преимущество   над
	Слабое преимущество   над  Почти слабое преимущество   над
	Существенное преимущество   над  Почти явное преимущество   над
	Почти существенное преимущество   над  Почти слабое преимущество   над

Этим экспертным высказываниям соответствуют следующие матрицы парных сравнений:

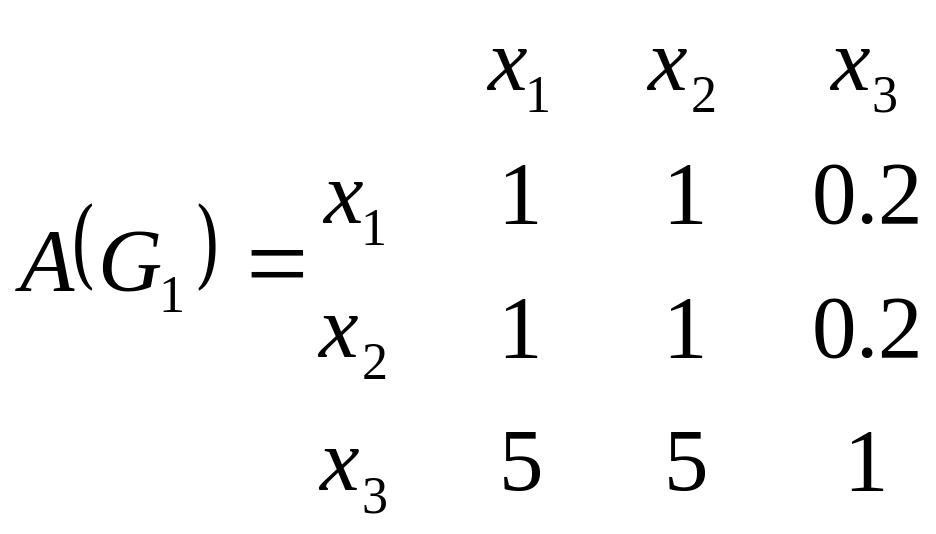
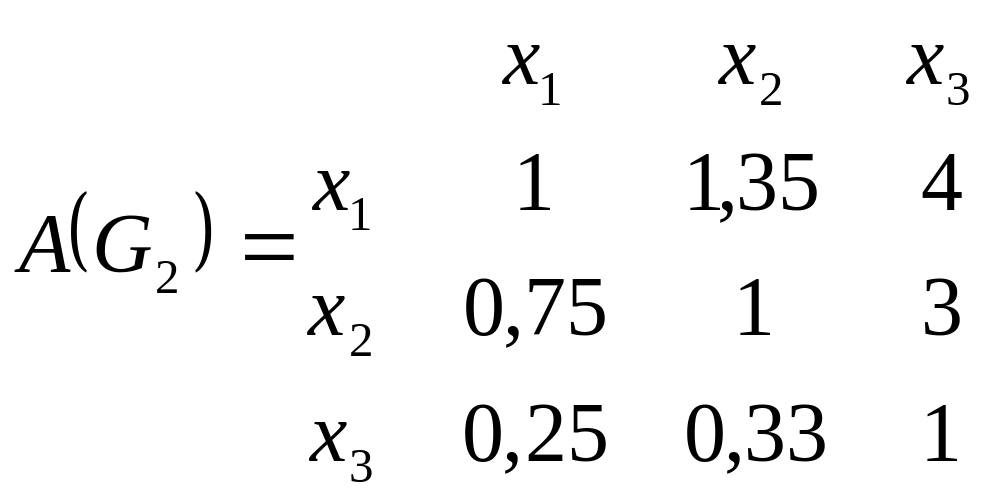
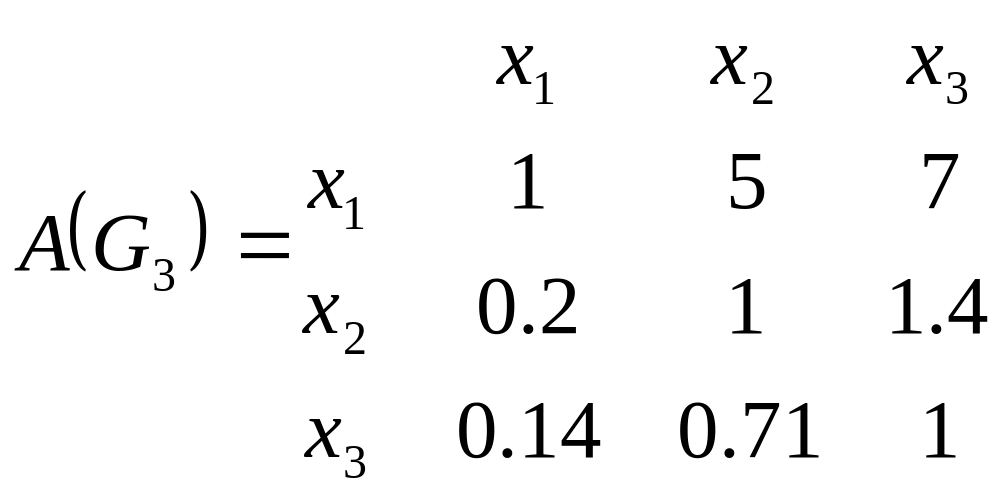
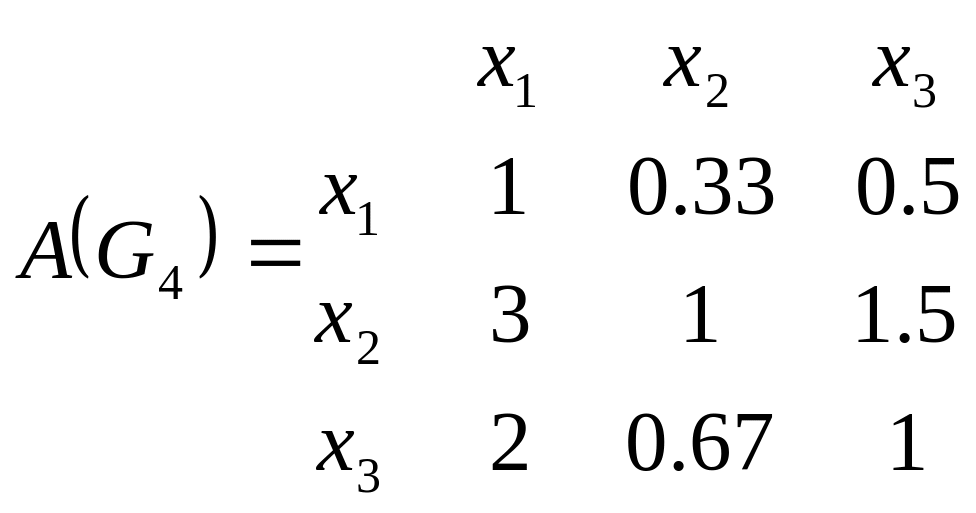
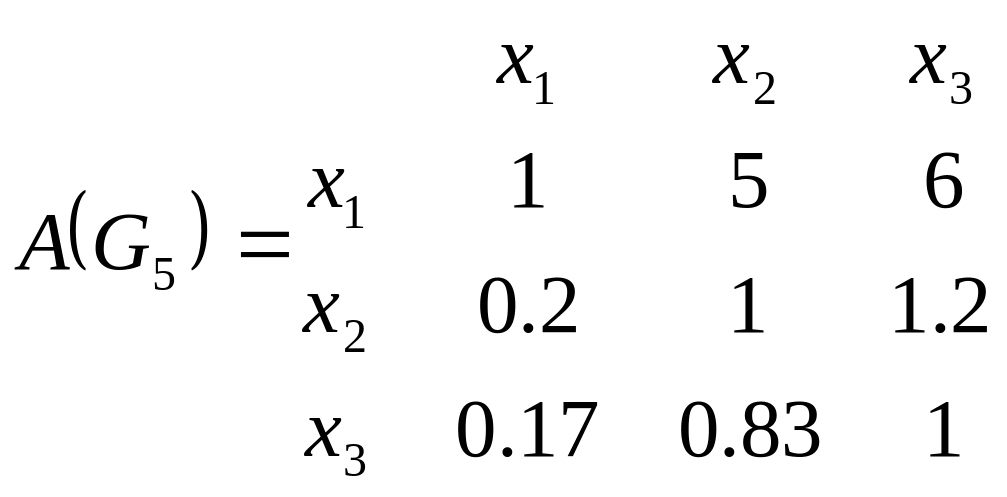
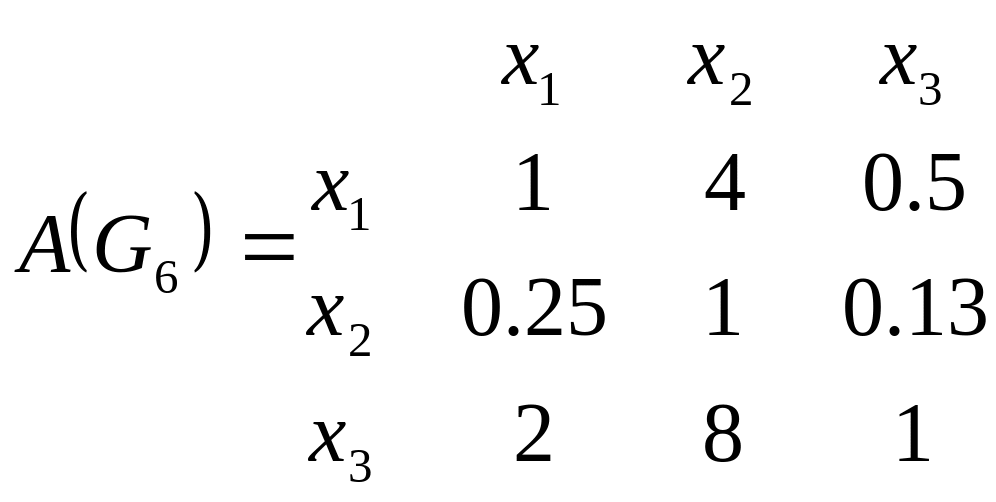
В этих матрицах полужирным шрифтом выделенные элементы, которые соответствуют парным сравнениям из табл. 5.1. Остальные элементы найдены в предположении о согласованости парных сравнений, т.е. с учетом того, что матрица парных сравнений является диагональной и обладает свойствами транзитивности и обратной симметричности.

Применяя формулу (5.8) к матрицами парных сравнений‚ получаем следующие нечеткие множества:

Теперь по формуле (5.9) получаем:

,

что свидетельствует о существенном преимуществе проекта   над проектом  , а также о слабом преимуществе проекта  над проектом  .

Предположим, что критерии   являются неравновесными. Для определения рангов критериев воспользуемся методом парных сравнений. Пусть заданы следующие лингвистические высказывания о важности критериев:

• почти существенное преимущество   над  ;

• явное преимущество   над  ;

• слабое преимущество   над  ;

• почти слабое преимущество   над  ;

• отсутствие преимущества   над  .

Этим экспертным высказываниям соответствует следующая матрица парных сравнений:

Применяя формулу (5.8), определим ранги критериев  :

; ;  ;  ;  ;  ,

что означает наибольшую важность приоритетности направления ( ) и степени проработки проекта ( ). По формуле (5.10) получаем такие нечеткие множества:

;

;

;

;

;

В результате пересечения нечетких множеств   получаем:

,

что свидетельствует о существенном преимуществе проекта   над проектами   и  , а также о слабом преимуществе проекта   над проектом  .

МОДУЛЬ 2