Описание лингвистической переменной

Постановка задачи: Пусть эксперт определяет калорийность продукта с помощью понятия «низкая», «средняя» и «высокая», при этом минимальная равняется 100 ккал, а максимальная – 500.

Формализация приведена с помощью лингвистической переменной.

Лингвистической переменной называется набор <β,T,X,G,M>, где

β – имя лингвистической переменной;

Т – множество его значений (терм-множество), представляющие имена нечетких переменных, областью определения, которых является множество X. Множество T называется базовым терм-множеством лингвистической переменной;

G – синтаксическая процедура, позволяющая оперировать элементами терм-множества T, в частности, генерировать новые термы (значения). Множество T∩G(T), где G(T) – множество сгенерированных термов, называется расширенным терм-множеством лингвистической переменной;

М – семантическая процедура, позволяющая преобразовать новое значение лингвистической переменной, образованной процедурой G, в нечеткую переменную, то есть сформировать соответствующее нечеткое множество.

β – калорийность продукта.

Τ = {«низкая», «средняя», «высокая»}

Х = [100;500]

G – процедура образования новых термов м помощью связок «и», «или» и модификаторов «очень», «слегка».

М – семантическая процедура задания на Х нечетких подмножеств: А₁ = «низкая калорийность», А₂ = «средняя калорийность», А₃ = «высокая калорийность», а также нечетких множеств из G(Т), соответствующих правилам трансляции связок и модификаторов. А₁= [100;260], А₂= [220;420], А₃= [380;500].

Вместе с рассмотренными выше базовыми значениями лингвистической переменной «рейтинг» (Т – {«низкая калорийность», «средняя калорийность», «высокая калорийность»}) существуют значения, зависящие от области определения Х. В данном случае значения лингвистической переменной «рейтинг ВУЗов» может быть определено в виде нечетких чисел, то есть «150 ккал», «300 ккал», «500 ккал».

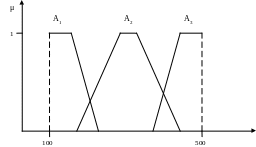
Рис. 2.6. Функция принадлежности нечетких множеств:

А₁ = «низкая калорийность», А₂ = «средняя калорийность», А₃ = «высокая калорийность»

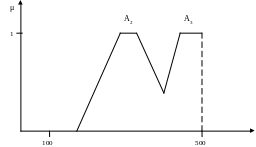
Рис. 2.7. Функция принадлежности: «средняя или высокая калорийность» = А2∩А3

Вывод: в ходе выполнения данной лабораторной работы были получены навыки работы с лингвистической переменной и представления ее в нечетком и графическом виде.

Варианты заданий:

1. Пусть эксперт определяет успеваемость студента с помощью понятия «низкая», «средняя» и «высокая», при этом минимальная успеваемость равняется 5 балам, а максимальная – 100.

2. Пусть эксперт определяет рейтинг ВУЗов с помощью понятия «низкий», «средний» и «высокий», при этом минимальный рейтинг равняется 1 балам, а максимальный – 5.

3. Пусть эксперт определяет калорийность продукта с помощью понятия «низкая», «средняя» и «высокая», при этом минимальная равняется 100 ккал, а максимальная – 500.

4. Пусть эксперт определяет уровень материального обеспечения клиента с помощью понятия «низкий», «средний» и «высокий», при этом минимальный уровень равняется 2000грн, а максимальная – 8000.

5. Пусть эксперт определяет размер внешнего долга страны с помощью понятия «низкий», «средний» и «высокий», при этом минимальный размер равняется 10 млрд грн, а максимальный – 300 млрд грн.

6. Пусть эксперт определяет уровень жизни в стране с помощью понятия «низкий», «средний» и «высокий», при этом минимальный уровень равняется 1 бал, а максимальный – 7.

7. Пусть эксперт определяет глубину колодца с помощью понятия «маленькая», «средняя» и «большая», при этом минимальная глубина равняется 4 м, а максимальная – 45.

8. Пусть эксперт определяет уровень безработицы с помощью понятия «низкий», «средний» и «высокий», при этом минимальный уровень равняется 10 тыс.чел. на 100 тыс. чел. Работоспособного возраста, а максимальный – 90 тыс.

9. Пусть эксперт определяет возраст художественной работы с помощью понятия «маленький», «средний» и «большой», при этом минимальный возраст равняется 10 лет, а максимальный – однозначно не задан.

10. Пусть эксперт определяет размер жесткого диска с помощью понятия «маленький», «средний» и «большой», при этом минимальный размер равняется 120 Гб, а максимальный – 1000.

11. Пусть эксперт определяет степень наполненности склада с помощью понятия «низкая», «средняя» и «высокая», при этом минимальный уровень равняется 10 тыс.изделий, а максимальный – 120 тыс.изделий.

12. Пусть эксперт определяет класс гостиницы с помощью понятия «низкий», «средний» и «высокий», при этом минимальный класс равняется 20 балам, а максимальный – 120.

13. Пусть эксперт определяет задолженность по квартплате с помощью понятия «маленькая», «средняя» и «высокая», при этом минимальный уровень равняется 1 тыс.грн, а максимальный – 30 тыс.грн.

14. Пусть эксперт определяет уровень IQ клиента с помощью понятия «низкий», «средний» и «высокий», при этом минимальный уровень равняется 10 балам, а максимальный – 200.

15. Пусть эксперт определяет цену мобильного телефона с помощью понятия «низкая», «средняя» и «высокая», при этом минимальный уровень равняется 300 грн, а максимальный – 8000 грн.

16. Пусть эксперт определяет возраст дерева с помощью понятия «молодое», «среднего возраста» и «старое», при этом минимальный возраст равняется 3 года, а максимальный – не определен.

17. Пусть эксперт определяет уровень эмоционального состояния клиента с помощью понятия «низкий», «средний» и «высокий», при этом минимальный уровень равняется 2 балам, а максимальный – 100.