Донецкий национальный технический университет

Институт информатики и искусственного интеллекта

Кафедра экономической кибернетики

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

для практичних робіт студентів з вибіркової навчальної дисципліни

циклу природничо-наукової та загальноекономічної підготовки

к лабораторным занятиям и организации работы студентов

по курсу „ Прикладні задачі моделювання економічних процесів ”

для студентів усіх форм навчання

Галузь знань: 0305 «Економіка та підприємництво»

Напрями підготовки: 6.030502 "Економічна кібернетика"

Укладач:

Донець О.С., к.е.н., доцент

Розглянуто на засіданні кафедри зовнішньоекономічної діяльності підприємств Протокол № 1 від 30 . 08 . 2013 р.

Донецьк, 2013

Методичні рекомендації для лабораторних робіт з дисципліни «Прикладні задачі моделювання економічних процесів» розроблено для студентів усіх форм навчання галузі знань 0305 «Економіка та підприємництво» напряму підготовки 6.030502 «Економічна кібернетика» (російською мовою) / Укл. О.C. Донець - Донецьк: ДонНТУ, 2013. - 84 с.

Методичні рекомендації до лабораторних занять підготовлено у відповідності до програми дисципліни «Прикладні задачі моделювання економічних процесів».

Методичні рекомендації містять зміст тем лабораторних робіт по кожній темі, методичні рекомендації та завдання.

У методичних рекомендаціях викладено загальні положення та тематичний зміст лабораторних робіт з вибіркової навчальної дисципліни «Прикладні задачі моделювання економічних процесів». Методичні рекомендації містять завдання щодо виконання лабораторних робіт з навчальної дисципліни «Математичні моделі в економіці».

Укладач:

О.С. Донець, к.е.н., доцент;

Рецензент:

Н.В. Касьянова, д.е.н., доцент

Відповідальний за випуск:

М.В. Румянцев, д.е.н., професор

Содерание

ВВЕДЕНИЕ 4

3. ЗАДАНИЯ К ЛАБОРАТОРНЫМ ЗАНЯТИЯМ 6

Лабораторная работа № 1 Тема: «Прикладные задачи анализа и оценивания параметров социально-экономических процессов. Работа с математическими функциями в Matlab Simulink» 6

Лабораторная работа № 2 14

Лабораторная работа № 3 21

Лабораторная работа № 4 31

Лабораторная работа № 6 53

Лабораторная работа № 7 66

Лабораторная работа № 8 73

4. ОРГАНИЗАЦИЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ 79

5. индивидуальная работа студентов 80

ЛИТЕРАТУРА 83

Введение

Практическая ценность изучения данного курса студентами специальности «экономическая кибернетика» состоит в формировании базовых навыков моделирования экономических процессов.

Цель: усвоение концептуальных положений построения математических моделей социально-экономических процессов на основе компьютерных технологий и их использования в анализе и управлении экономическими системами.

Задание: изучение инструментария решения прикладных задач моделирования и анализа социально-экономических процессов с использованием теории случайных процессов, нечеткой логики, сетевого управления и применения компьютерных технологий.

Предмет: методология и инструментарий построения и применения прикладных математических моделей анализа и управления экономическими процессами.

Студенты должны уметь:

Представлять основные этапы построения модели. Самостоятельно определять задачи на каждом из этапов. Осуществлять планирование практического эксперимента модели и формирование выводов о ее практической значимости с целью внесения корректировок и новых допущений.

Сформировать четкое представление о формировании баз знаний в рамках теории нечеткой логики. Выполнять свободное построение лингвистических переменных, описывающих заданный экономический процесс (систему). Сформировать навыки разработки блоков фазификации и дефазификации при моделировании систем. Уметь преобразовывать данные экономической статистки и экспертной информации в базисы нечетких переменных и множеств.

2. Модульно-тематическая программа курса

7- семестра

№п/п	Название тем лекций и лабораторных работ	Количество часов(*)
		ЭК
		Л	Лр	Ср	І
Модуль 1. Математические основы моделирования экономики при помощи нечеткой логики		16	16	20	23
1	Прикладные задачи анализа и оценки параметров социально-экономических процессов.	2	2	4	-
2	Нечеткая логика.	4	2	4	-
3	Построение функций принадлежности на основе экспертной информации.	4	4	4	-
4	Синтез баз нечетких знаний для анализа и моделирования экономических систем в среде Matlab.	4	4	4	-
5	Нечеткий метод анализа иерархий. Принятие решений в нечетких условиях по схеме Беллмана – Заде.	2	4	4	-
6	Комплексный отче по модулю №1	-	-	-	23
		-	-	-	-
Модуль 2. Методы и модели управления экономикой		16	16	20	23
9	Нечеткое моделирование конкурентоспособности товара при помощи Fuzzy Logic Toolbox.	4	4	4	-
10	Финансовый анализ и оценка риска банкротства средствами Fuzzy Logic.	4	4	4	-
11	Модели управления запасами.	2	2	4	-
12	Элементы теории случайных процес- сов и их использование для решения прикладних задач.	3	3	4	-
13	Оптимизационные задачи управления экономическими системами на основе применения теории сетей.	3	3	4	-
14	Комплексный отчет по модулю №2	-	-	-	23
21	ВСЕГО ЧАСОВ	32	32	40	46

(*) Количество часов может быть изменено в соответствии учебному плану специальности

3. ЗАДАНИЯ К ЛАБОРАТОРНЫМ ЗАНЯТИЯМ

МОДУЛЬ 1

Лабораторная работа № 1 Тема: «Прикладные задачи анализа и оценивания параметров социально-экономических процессов. Работа с математическими функциями в Matlab Simulink»

Цель 1: Студенты должны усвоить и овладеть навыками работы в среде Matlab. Для заданной экономической системы научиться определять проблему, разрабатывать рабочую гипотезу и постановку задачи. Определять проблемную систему. Разработать в среде Simulink модель, которая позволяет определять оптимальную ставку налога на прибыль. Научиться делать обоснованные экономические выводы и рекомендации.

Ход выполнения работы:

Блоки Display и Scope предназначены для вывода на экран результатов вычисления функций, соответственно в числовом и графическом виде.

В системе Matlab определены следующие математические функции:

Abs(X) – возвращает абсолютную величину для каждого числового элемента вектора X. Если Х содержит комплексные числа, abs (X) вычисляет модуль каждого числа.

Рис.1.1. Пример использования блока Abs

Усилители Gain и Matrix Gain выполняют умножение входного сигнала на постоянный коэффициент. Параметры:

• Gain – Коэффициент усиления.

• Multiplication – Способ выполнения операции.

Блоки усилителей Gain и Matrix Gain есть один и тот же блок, но с разными начальными установками параметра Multiplication.

Параметр блока Gain может быть положительным или отрицательным числом, как больше, так и меньше 1. Коэффициент усиления можно задавать в виде скаляра, матрицы или вектора, а также в виде вычисляемого выражения.

В том случае если параметр Multiplication задан как Element-wise K*u, то блок выполняет операцию умножения на заданный коэффициент скалярного сигнала или каждого элемента векторного сигнала. В противном случае блок выполняет операцию матричного умножения сигнала на коэффициент заданный матрицей. По умолчанию коэффициент усиления является действительным числом типа double.

Для операции поэлементного усиления входной сигнал может быть скалярным, векторным или матричным любого типа, за исключением логического (boolean). Элементы вектора должны иметь одинаковый тип сигнала. Выходной сигнал блока будет иметь тот же самый тип, что и входной сигнал. Параметр блока Gain может быть скаляром, вектором или матрицей любого типа, за исключением логического (boolean).

При вычислении выходного сигнала блок Gain использует следующие правила:

1. Если входной сигнал действительного типа, а коэффициент усиления комплексный, то выходной сигнал будет комплексным.

2. Если тип входного сигнала отличается от типа коэффициента усиления, то Simulink пытается выполнить приведение типа коэффициента усиления к типу входного сигнала. В том случае, если такое приведение невозможно, то расчет будет остановлен с выводом сообщения об ошибке. Такая ситуация может возникнуть, например, если входной сигнал есть беззнаковое целое (uint8), а параметр Gain задан отрицательным числом.

Рис.1.2. Пример использования блока Gain

Блок вычисления суммы Sum выполняет вычисление суммы текущих значений сигналов. Параметры:

• Icon shape – Форма блока. Выбирается из списка (Round – окружность, rectangular – прямоугольник).

• List of sign – Список знаков. В списке можно использовать следующие знаки: + (плюс), - (минус) и | (разделитель знаков).

• Saturate on integer overflow (флажок) – Подавлять переполнение целого. При установленном флажке ограничение сигналов целого типа выполняется корректно.

Количество входов и операция (сложение или вычитание) определяется списком знаков параметра List of sign, при этом метки входов обозначаются соответствующими знаками. В параметре List of sign можно также указать число входов блока. В этом случае все входы будут суммирующими.

Если количество входов блока превышает 3, то удобнее использовать блок Sum прямоугольной формы.

Блок может использоваться для суммирования скалярных, векторных или матричных сигналов. Типы суммируемых сигналов должны совпадать. Нельзя, например, подать на один и тот же суммирующий блок сигналы целого и действительного типов.

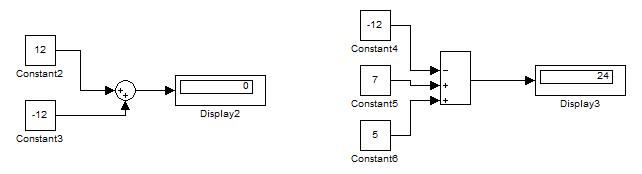
Рис.1.3. Пример использования блока Sum

Блок умножения Product предназначен для вычисления произведения текущих значений сигналов. Параметры:

• Number of inputs – Количество входов. Может задаваться как число или как список знаков. В списке знаков можно использовать знаки * (умножить) и / (разделить).

• Multiplication – Способ выполнения операции. Может принимать значения: Element-wise – поэлементный; Matrix – матричный.

• Saturate on integer overflow (флажок) – Подавлять переполнение целого. При установленном флажке ограничение сигналов целого типа выполняется корректно.

Если параметр Number of inputs задан списком, включающим кроме знаков умножения также знаки деления, то метки входов будут обозначены символами соответствующих операций.

Блок может использоваться для операций умножения или деления скалярных векторных или матричных сигналов. Типы входных сигналов блока должны совпадать.

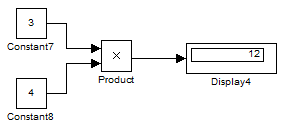
Рис.1.4. Пример использования блока Product

Блок определения минимального или максимального значения MinMax. Определяет максимальное или минимальное значение из всех сигналов, поступающих на его входы. Параметры:

• Function - Выходной параметр. Выбирается из списка:

• min – Минимальное значение.

• max – Максимальное значение.

• Number of input ports – Количество входных портов.

Входные сигналы блока могут быть скалярными или векторными. Блок определяет максимальное или минимальное значение из всех скалярных сигналов, поступающих на его входы. Если входные сигналы являются векторными, то блок выполняет поэлементную операцию поиска минимального или максимального значения. В этом случае размерности векторов должны совпадать. Если количество входных портов блока задано равным 1, то блок может использоваться для нахождения минимального или максимального значения во входном векторе.

Рис.1.5. Пример использования блока MinMax

Блок вычисления математических функций Math Function. Выполняет вычисление математической функции. Параметры:

• Function – Вид вычисляемой функции (выбирается из списка):

• exp – Экспоненциальная функция;

• log – Функция натурального логарифма;

• 10^u – Вычисление степени 10;

• log10 – Функции логарифма;

• magnitude^2 – Вычисление квадрата модуля входного сигнала;

• square – Вычисление квадрата входного сигнала;

• sqrt – Квадратный корень;

• pow – Возведение в степень;

• conj – Вычисление комплексно-сопряженного числа;

• reciprocal – Вычисление частного от деления входного сигнала на 1;

• hypot –Вычисление корня квадратного из суммы квадратов входных сигналов (гипотенузы прямоугольного треугольника по значениям катетов);

• rem – Функция, вычисляющая остаток от деления первого входного сигнала на второй;

• mod – Функция, вычисляющая остаток от деления с учетом знака;

• transpose – Транспонирование матрицы;

• hermitian – Вычисление эрмитовой матрицы.

• Output signal type – Тип выходного сигнала (выбирается из списка):

• auto – Автоматическое определение типа;

• real –Действительный сигнал;

• complex- Комплексный сигнал.

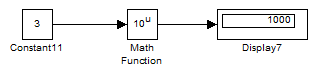
Рис.1.6. Пример использования блока Math Function

Блок округления числового значения Rounding Function. Выполняет операцию округления числового значения. Параметры:

Function – Способ округления (выбирается из списка):

• floor – Округление до ближайшего меньшего целого.

• ceil – Округление до ближайшего большего целого.

• round – Округление до ближайшего целого.

• fix – Округление отбрасыванием дробной части.

Входные сигналы блока могут быть скалярными, векторными или матричными действительного и комплексного типа. При векторном или матричном входном сигнале блок выполняет поэлементные операции.

Выходной сигнал блока будет иметь тип double или single.

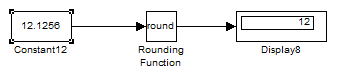
Рис.1.7. Пример использования блока Rounding Function

Вывод: в ходе выполнения работы были получены навыки работы с математическими функциями в среде Simulink.

Цель 2: методами имитационного моделирования определить оптимальную ставку налогообложения прибыли, используя метод поиска на сетке факторов. Планирование эксперимента заключается в изменении факторов с постоянным шагом и построении экспериментальных графиков зависимости ставки от фактора. Оптимальные величины ставок определяются не алгоритмически, а визуально по графикам.

Ход выполнения работы:

1. Определение проблемы.

Государство стремится увеличить налоги, чтобы наполнить бюджет для выполнения своих социально-экономических и оборонных функций. Бизнес недоволен текущим налогообложением и требует уменьшения налоговых ставок. Экономисты утверждают, что большие налоги сдерживают развитие экономики, а значит и будущее наполнение бюджета.

Проблема: не существует обоснования величин, приемлемых для всех налоговых ставок.

2. Уточнение и ограничение проблемы.

Несмотря на массу налогов, и терминов, источником развития бизнеса и источником налогового наполнения бюджета, конечной инстанцией является прибыль предприятия, поэтому исследуем лишь ставку налога на прибыль.

3. Рабочая гипотеза.

Поступления в бюджет за определенный период времени будут наибольшими не при максимальной, а при оптимальной для бюджета ставки налога. С ростом налоговой ставки, поступления в бюджет будут увеличиваться, а потом уменьшаться.

4. Постановка задачи.

Исследовать зависимость поступлений в бюджет от величины налоговой ставки на прибыль, используя математическое моделирование.

5. Определение проблемной системы.

В проблемную систему включаем объекты, их взаимосвязи и показатели, от которых зависит решение проблемы. Законодательство определяет ставку налога. Бюджет получает налоговые отчисления от прибыли предприятий. Фирмы обладают собственным капиталом, производят прибыль, отчисляют по налоговой ставке средства в бюджет.

Постналоговая прибыль, как нераспределенная, полностью включается в собственный капитал фирмы, дивиденды не включаются, никаких других отчислений от прибыли не производится. Вся прибыль распределяется только на 2 потока: бюджет и капитал фирмы.

6. Математическая модель элементов системы.

, (1.1)

где – сумма поступивших в бюджет средств от момента начала моделирования к концу Т, грн.;

– доналоговая прибыль полученная предприятием, грн./год.;

– ставка налога на прибыль;

– время (для запасов это момент, т.е. конец года, а для потоков это интервал времени определенного года);

– начальный интервал моделирования;

– конечный интервал моделирования.

_{, (1.2)}

, (1.3)

где – капитализированный предприятием за период моделирования остаток прибыли;

– рентабельность капитала предприятия.

Математическая модель в непрерывном времени:

. (1.4)

Данная модель была реализована в MatLab SIMULINK.

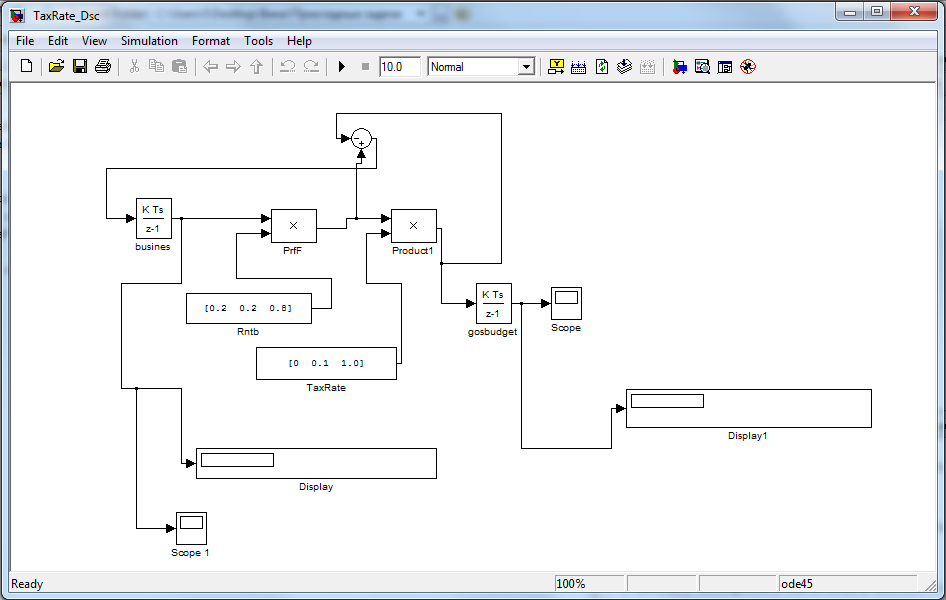
Рис. 1.8. Имитационная модель определения оптимальной ставки налогообложения

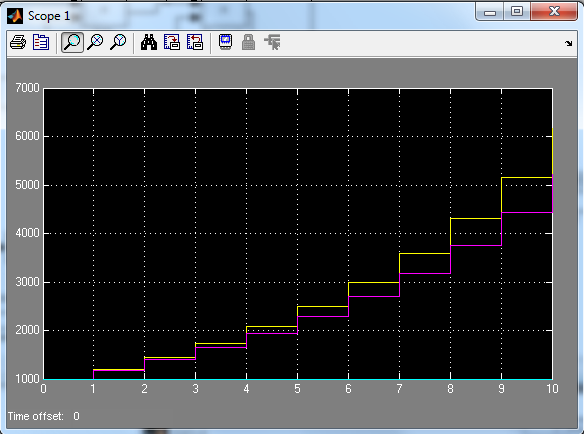
Рис. 1.9. График капитализированной прибыли предприятия

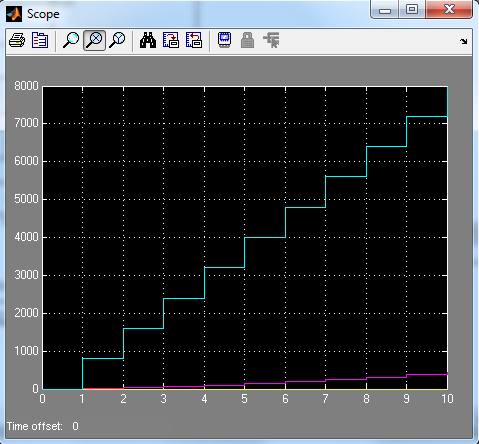
Рис. 1.10. График поступивших в бюджет средств

Выводы: В ходе выполнения данной лабораторной работы были получены навыки работы в сред Matlab-Simulink. Была построена модель для определения оптимальной ставки налога и получены графики дохода фирмы и средств, поступающих в бюджет при разных значениях налоговой ставки.