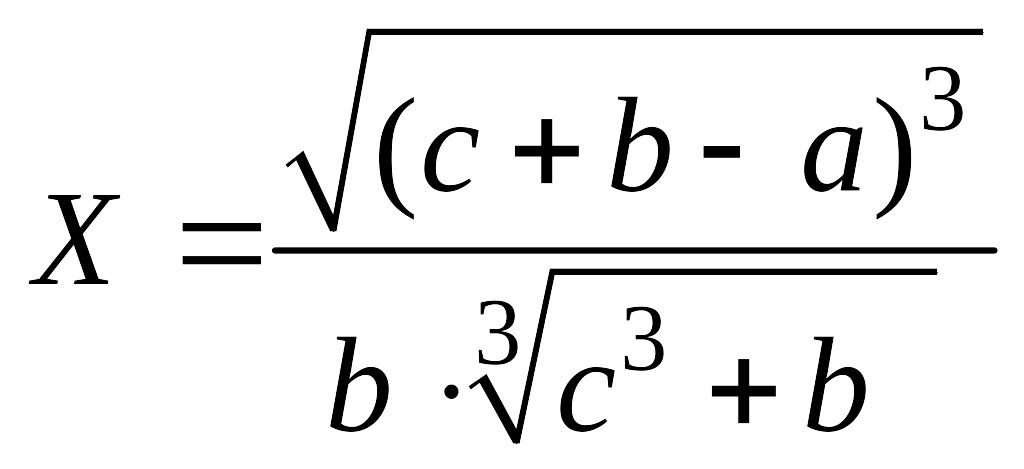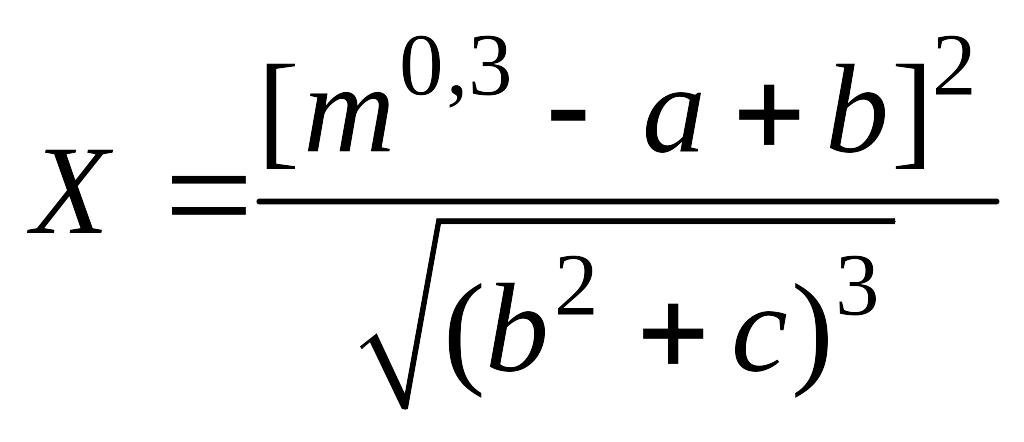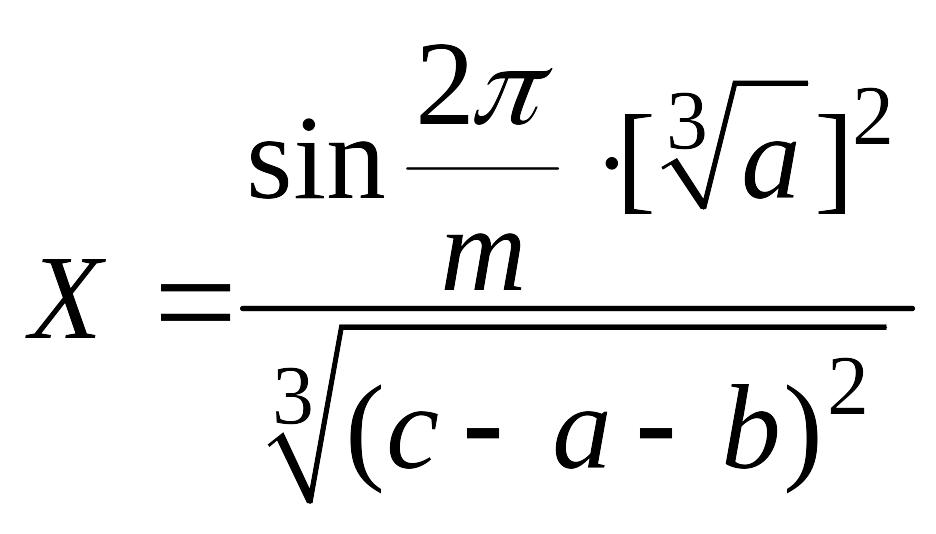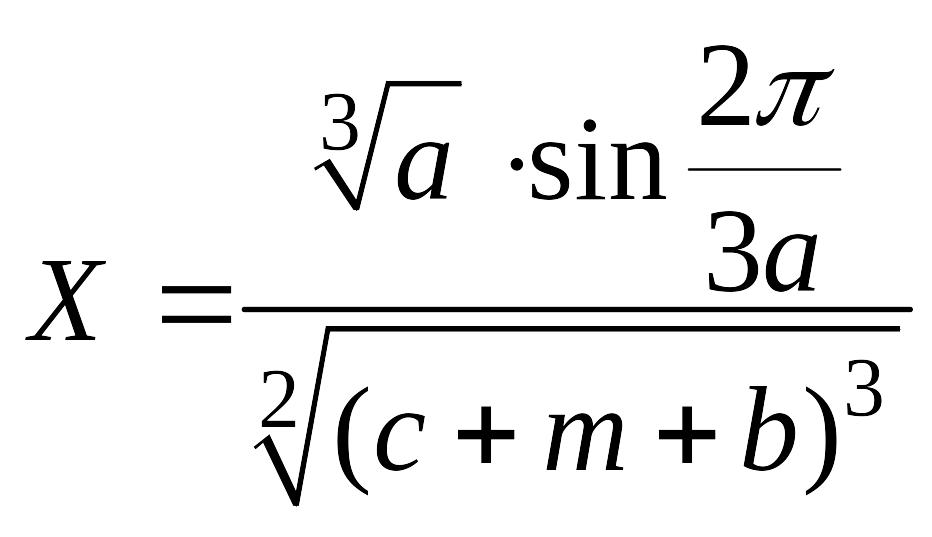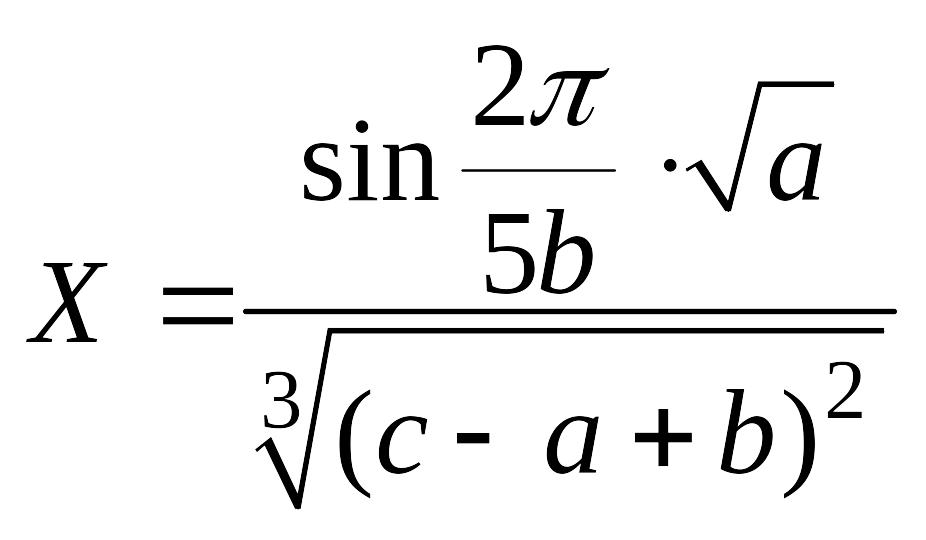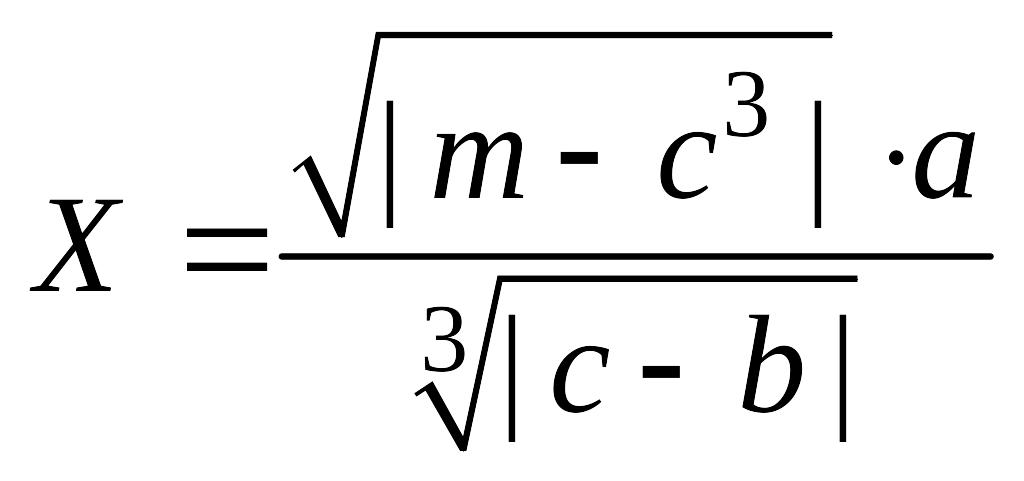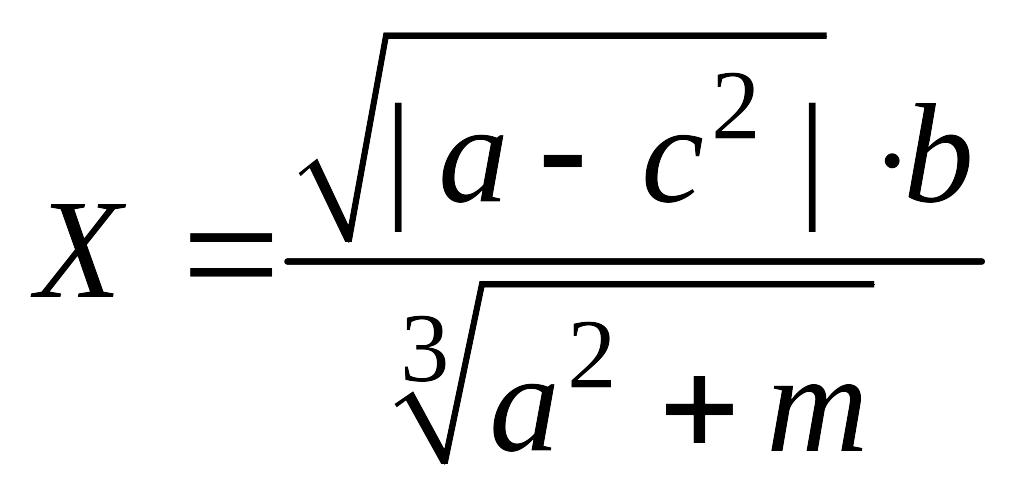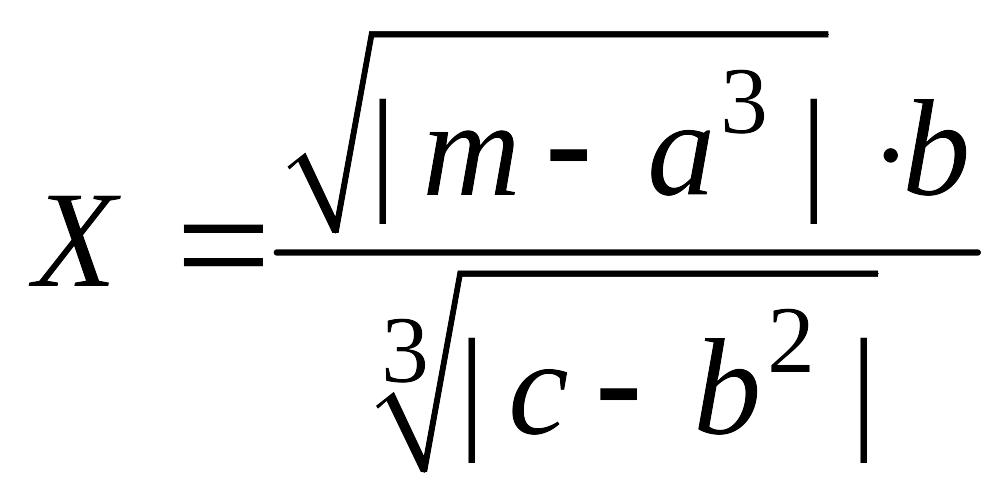Темы домашних контрольных работ

1. Контрольная работа №1

Тема: Элементы теории погрешностей.

2. Контрольная работа №2

Тема: Приближенное решение нелинейных уравнений.

Задание. Лабораторные работы № 3-5.

3. Контрольная работа №3

Тема: Интерполирование. Обратное интерполирование. Численное дифференцирование.

Задание. Лабораторные работы № 8-10.

Задание к домашней контрольной работе №1

1. Элементы теории погрешностей.

Задание из Таблицы №1:

а) Определить какое равенство точнее.

б) Округлить сомнительные цифры числа, оставив верные знаки: 1) в узком смысле; 2) в широком смысле. Определить предельные абсолютную и относительную погрешности результата.

в) Найти предельные абсолютную и относительную погрешности чисел, если они имеют только верные цифры: 1) в узком смысле; 2) в широком смысле.

Таблица № 1

№	а)	б)
		1	2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60

№	в)			№	в)
	1	2			1	2
1				31
2				32
3				33
4				34
5				35
6				36
7				37
8				38
9				39
10				40
11				41
12				42
13				43
14				44
15				45
16				46
17				47
18				48
19				49
20				50
21				51
22				52
23				53
24				54
25				55
26				56
27				57
28				58
29				59
30				60

Образец выполнения задания А1.

A1. a) Какое равенство точнее .

Обозначим , ; , .

Тогда , ,

, .

Так как , то равенство определено точнее.

Ответ: Равенство определено точнее.

б) Округлить сомнительные цифры числа, оставив верные знаки: 1) в узком смысле; 2) в широком смысле. Определить предельные абсолютную и относительную погрешности результата.

1. Дано приближенное число 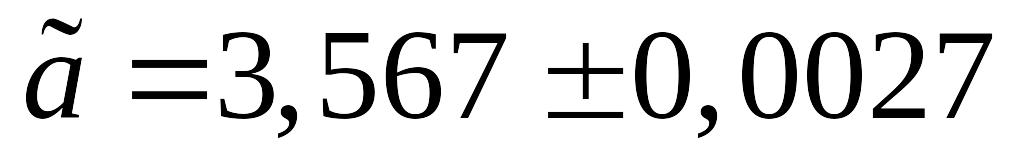, где .

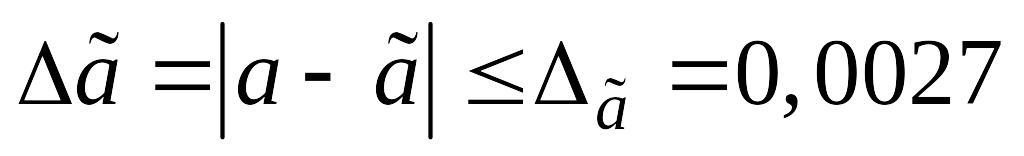Определим число верных знаков в узком смысле, используя следующее выражение

.

Так как , и верно неравенство , то получим , . Округлим до трех верных знаков и получим с погрешностью округления . При этом погрешность полученного приближенного числа равен .

Определим число верных знаков приближенного числа .

, , . Округлим до двух верных знаков и получим с погрешностью округления . При этом погрешность полученного приближенного числа равна .

Определим число верных знаков приближенного числа .

, , . Так как , то приближенное число имеет только верные знаки.

Определим предельную относительную погрешность приближенного числа . Для этого используем определение предельной погрешности: , .

Тогда получим .

Ответ: , .

2. Дано приближенное число 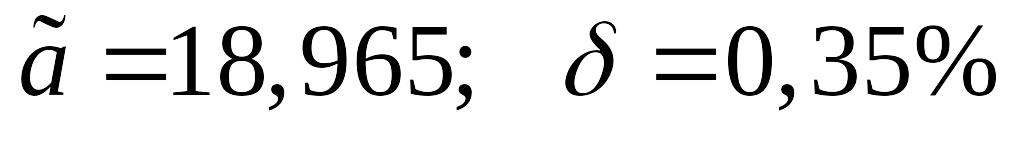, где 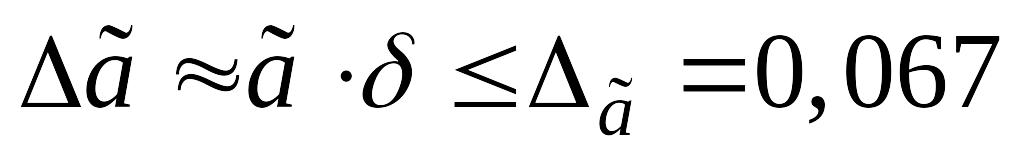. Определим число верных знаков в широком смысле, используя следующее выражение .

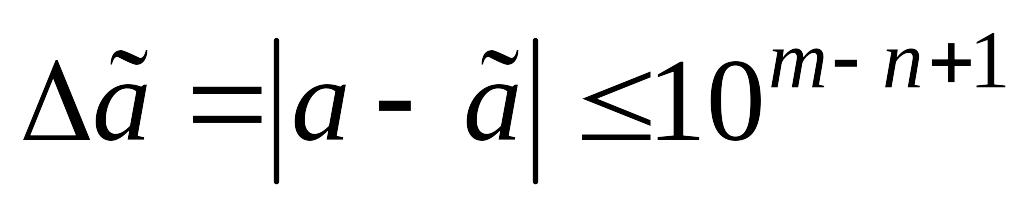Так как , и верно неравенство , то получим , . Округлим до трех верных знаков и получим с погрешностью округления . При этом погрешность полученного приближенного числа равна .

Определим число верных знаков приближенного числа . , , . Округлим до двух верных знаков и получим с погрешностью округления . При этом погрешность полученного приближенного числа равна .

Определим число верных знаков приближенного числа .

Из условия , получим , . Так как , то приближенное число имеет только верные знаки.

Определим предельную относительную погрешность приближенного числа . Для этого используем определение предельной погрешности: , .

Тогда получим .

Ответ: , .

в) Найти предельные абсолютную и относительную погрешности чисел, если они имеют только верные цифры: 1) в узком смысле; 2) в широком смысле.

1) Дано приближенное число .

Так как это число имеет только верные цифры в узком смысле, то . Определим предельную абсолютную погрешность числа из выражения . Тогда .

Следовательно, для предельной абсолютной погрешности имеем . Для определения предельной относительной погрешности числа можно использовать выражение .

Так как , то .

Ответ: .

2) Дано приближенное число .

Так как это число имеет только верные цифры в широком смысле, то . Определим предельную абсолютную погрешность числа из выражения . Тогда .

Следовательно, для предельной абсолютной погрешности имеем . Для определения предельной относительной погрешности числа можно использовать выражение .

Тогда получим .

Ответ: .

2. Элементы теории погрешностей.

a) Вычислить и определить предельные абсолютную и относительную погрешности результата.

b) Вычислить и определить предельные абсолютную и относительную погрешности результата.

c) Вычислить и определить предельные абсолютную и относительную погрешности результата пользуясь общей формулой погрешности: 1) в узком смысле; 2) в широком смысле.

Задание из Таблицы 2 определяется по следующей схеме:

Если , то номер задания равен номеру варианта ( ), а исходные данные из Кол.1;

Если , то номер задания равен ( ), а исходные данные из Кол.2;

Если , то номер задания равен ( ), а исходные данные из Кол.3;

Если , то номер задания равен ( ), а исходные данные из Кол.4.

Таблица 2

№	Формулы		Кол. 1	Кол. 2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

№	Формулы		Кол. 3	Кол. 4
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

Образец выполнения задания А2.

а) Вычислить и определить предельные абсолютную и относительную погрешности результата. Исходное выражение , где , , , .

По правилам вычисления погрешностей арифметических выражений и функций имеем

,

.

Для определения предельной абсолютной погрешности выражения используем формулу . Тогда получим

, .

Определим число верных знаков в вычисленном выражении в широком смысле, используя предельную абсолютную погрешность . Тогда имеем , , . Округлим результат до верного знака , при этом погрешность округления равен . Тогда . Определим число верных знаков в : , . Следовательно, в остались только верные знаки. Определим предельную относительную погрешность числа : .

Ответ: .

b) Выполняется аналогично пункту а).

c) Вычислить и определить предельные абсолютную и относительную погрешности результата пользуясь общей формулой погрешности: 1) в узком смысле; 2) в широком смысле.

Исходное выражение , где , , .

Тогда по общей формуле погрешностей имеем

; , , .

.

.

Определим число верных знаков в значении .

, .

Следовательно, необходимо округлить до верных знаков

.

.

Вычислим предельную относительную погрешность результата

.

Ответ: .