Вариант № 1
1. Вычислить:
.
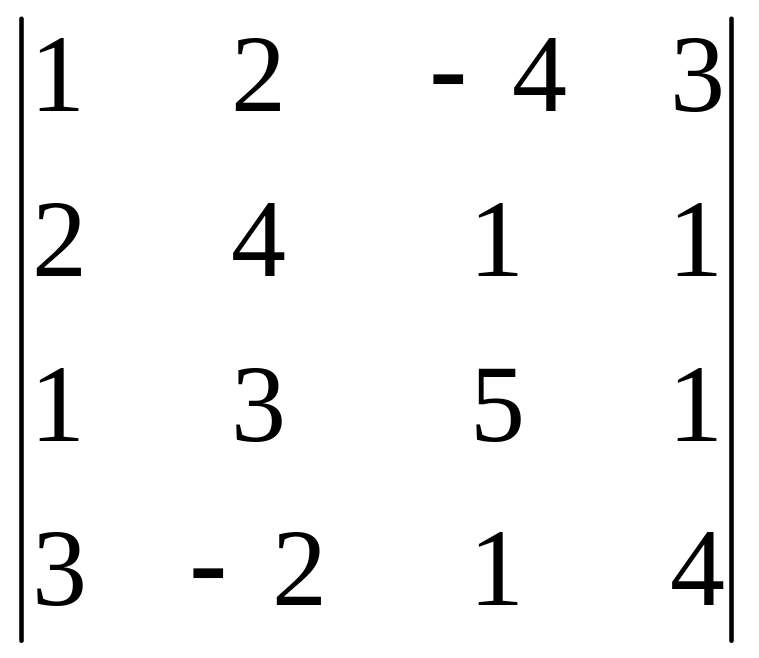2.
.
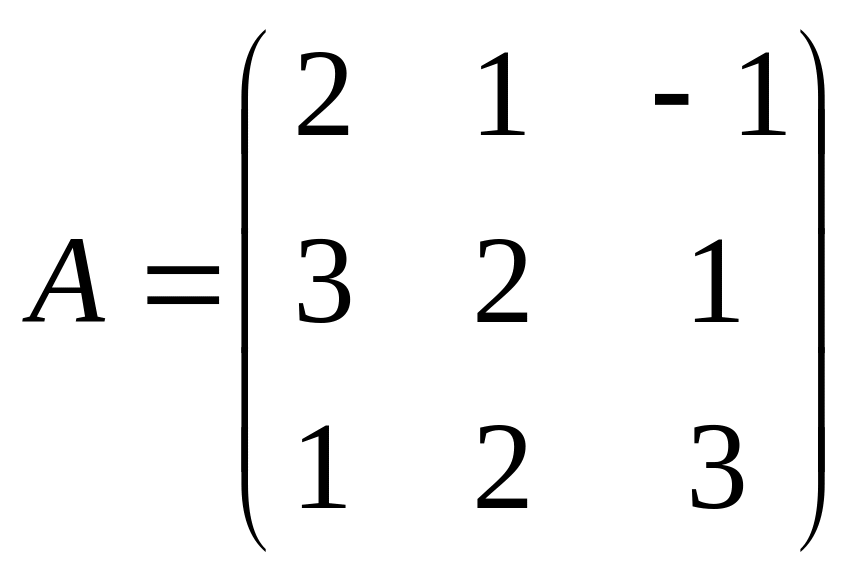3. Решить
систему уравнений
.
4. Даны
вершины треугольника
,
.
Написать уравнение высоты BD.
Найти пределы
5.
6.
Провести полное исследование и построить графики функций:
7.
8.
Вычислить
интегралы: 9.
10.
11.
Найти экстремум функции
12. В каждом из трех заданий теста по теории вероятности предложены 4 варианта ответа, из которых только один правильный. Студент не подготовился к тесту и, пытаясь угадать ответ, выбирает его случайным образом. Найти вероятность того, что студент верно ответит на все три вопроса теста
13. Дан ряд распределения случайной величины X.
X |
0 |
1 |
3 |
6 |
7 |
P |
0.1 |
0.2 |
0.2 |
0.1 |
? |
Построить функцию распределения. Найти математическое ожидание, дисперсию, среднее квадратическое отклонение.
14. Случайная величина X подчинена закону распределения с плотностью:
Найти коэффициент a, математическое ожидание и дисперсию.
Вариант № 2
1. Вычислить
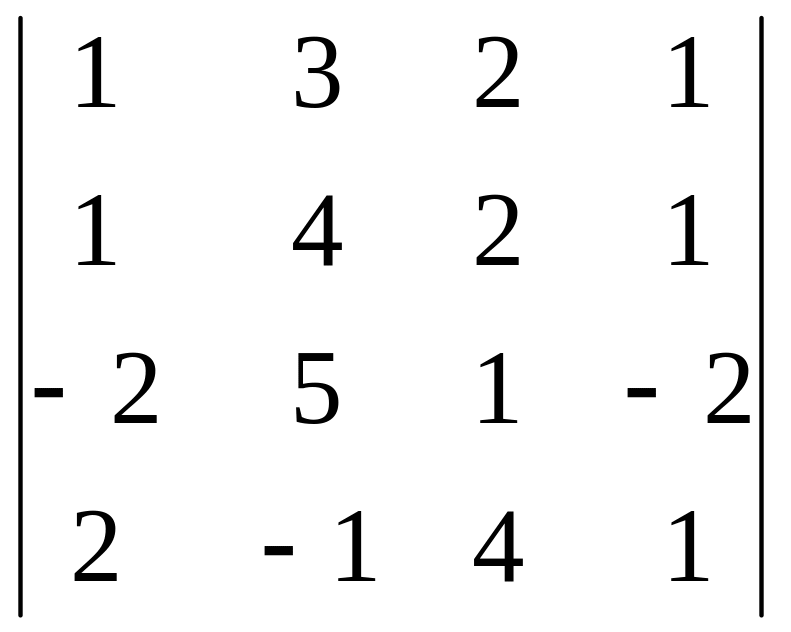. 2.
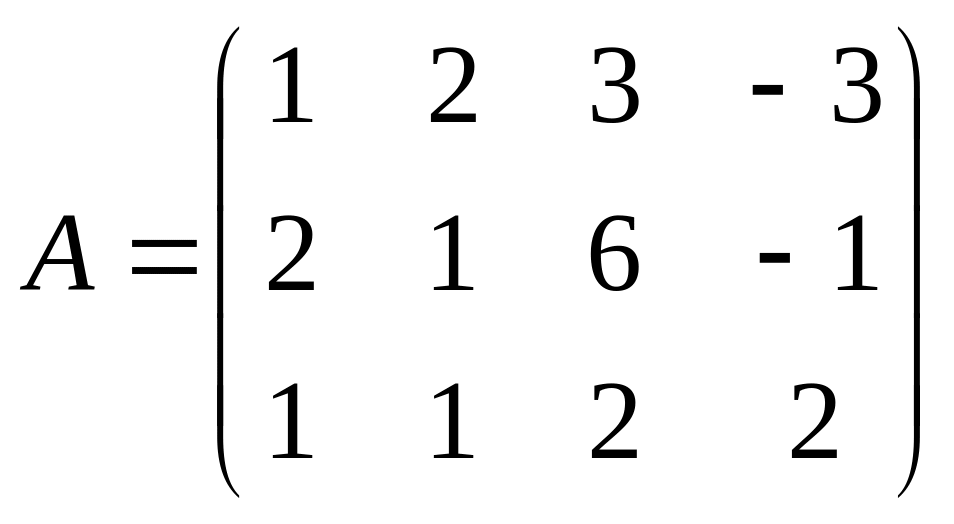rangA=?
3. Решить систему уравнений
4. Найти площадь параллелограмма, построенного на векторах
и
Найти пределы
5.
6.
Провести полное исследование и построить графики функций:
7.
8.
Вычислить
интегралы: 9.
10.
11. Найти
частные производные
.
12. Между двумя городами курсируют три поезда: «купейный», «плацкартный» и «СВ». Вероятность того, что «купейный» поезд придет вовремя 0,9, «плацкартный» - 0,7 и «СВ» - 0,95. Вероятность того, что пассажир приобретет билет на «плацкартный» поезд – 0,2, «купейный» - 0,5, «СВ» - 0,3. Найти вероятность того, что пассажир прибудет в пункт назначения вовремя.
13. Дан ряд распределения случайной величины X.
X |
1 |
2 |
4 |
5 |
7 |
p |
0,1 |
0,2 |
0,3 |
? |
0,4 |
Построить функцию распределения. Найти математическое ожидание и дисперсию,
14. Плотность вероятности случайной величины X имеет вид:
.
Определить A, математическое
ожидание и дисперсию случайной величины
X.
Вариант № 3
1. Вычислить
.
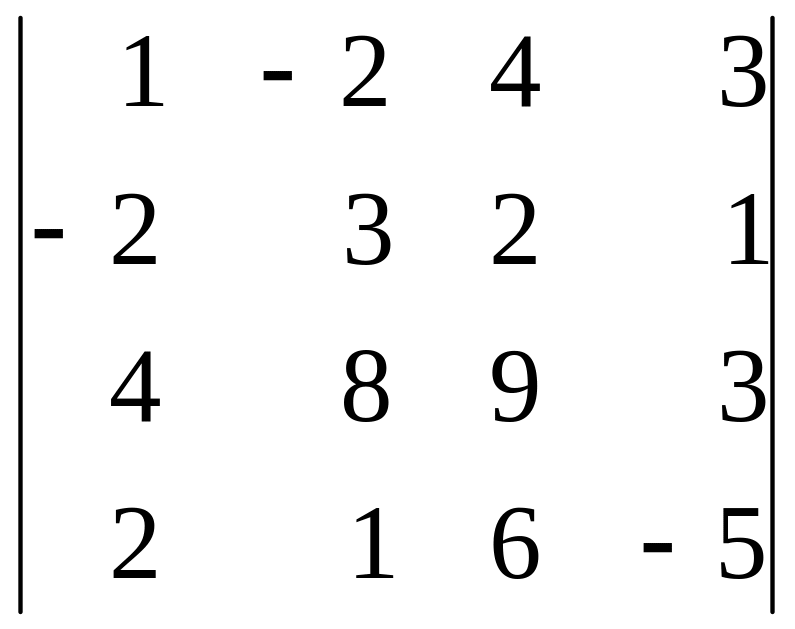2.
.
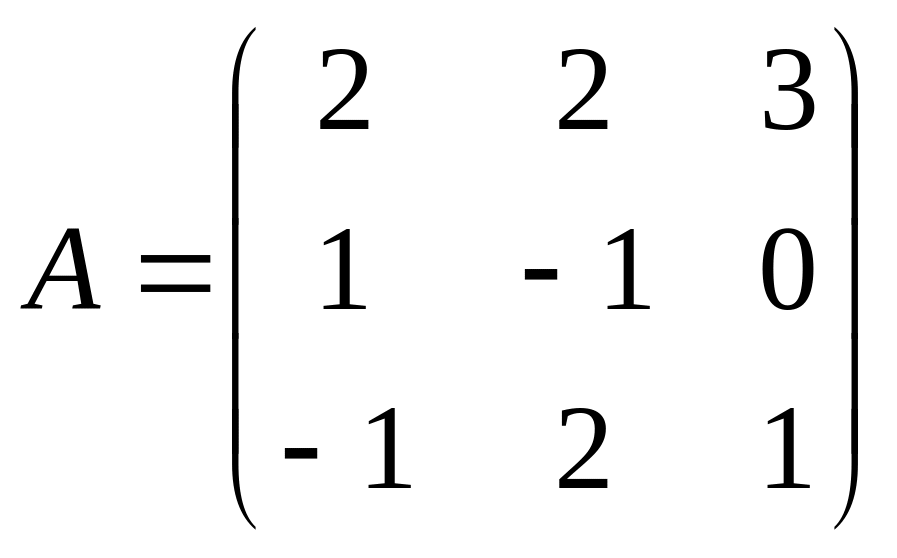3. Решить систему уравнений
4. Найти
расстояние от точки
до прямой
.
Найти пределы
5.
6.
Провести полное исследование и построить графики функций:
7.
8.
Вычислить
интегралы 9.
10.
11. Найти
дифференциал второго порядка
12. В каждом из трех заданий теста по теории вероятности предложены 4 варианта ответа, из которых только один правильный. Студент не подготовился к тесту и, пытаясь угадать ответ, выбирает его случайным образом. Найти вероятность того, что студент верно ответит хотя бы на один вопрос теста.
13. Дан ряд распределения случайной величины X.
X |
-4 |
-1 |
0 |
2 |
5 |
p |
0,1 |
0,05 |
0,05 |
0,4 |
? |
Построить функцию распределения. Найти математическое ожидание, дисперсию.
14.
Случайная величина Х имеет плотность
распределения
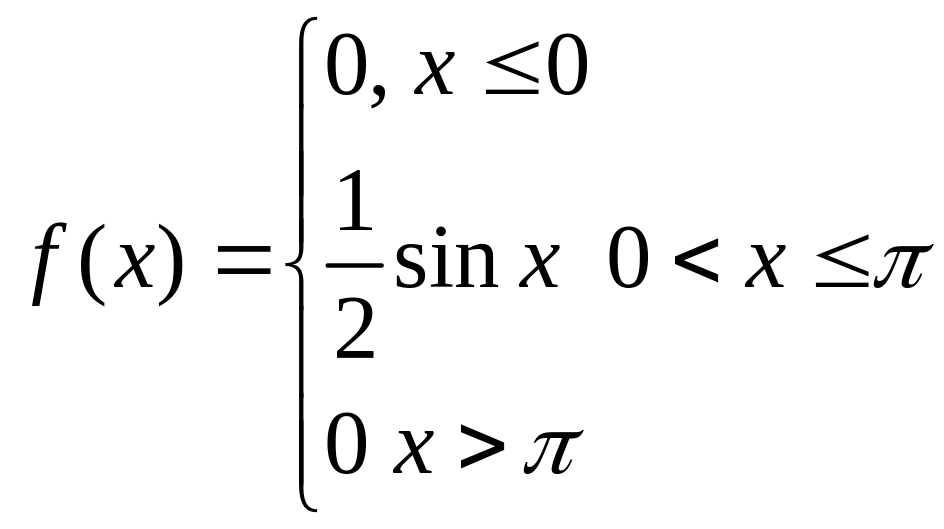Найти функцию распределения.
Вариант № 4
1.. Вычислить:
.
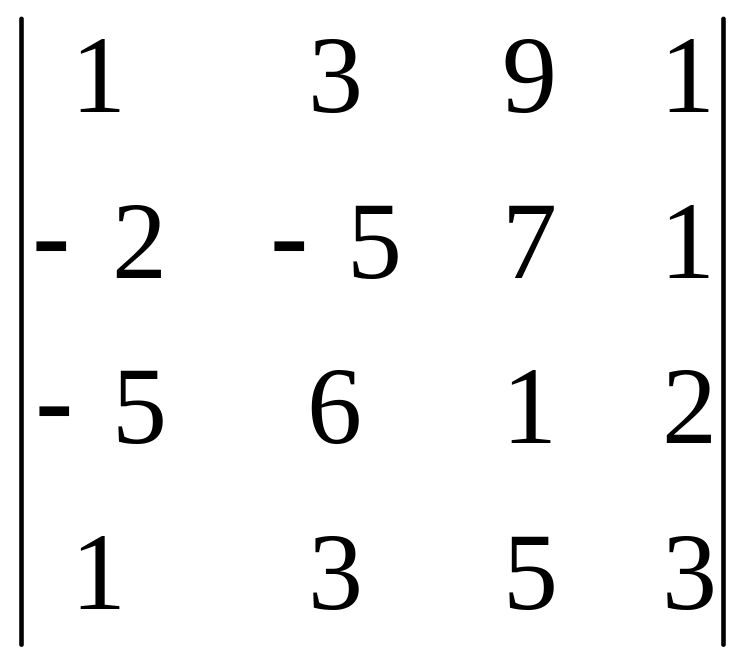2.
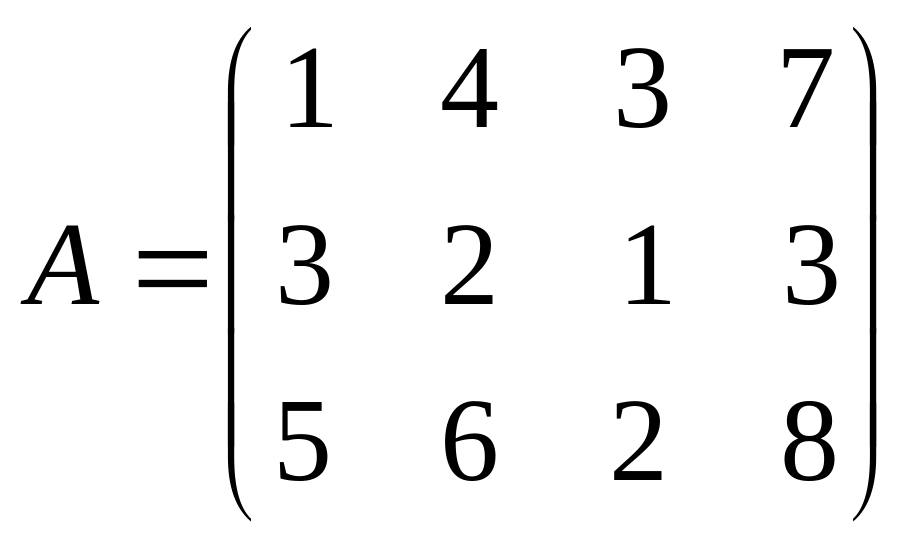rangA=?
3. Решить систему уравнений
4. Найти
площадь параллелограмма, построенного
на векторах
и
,
где
и
-
единичные векторы, образующие угол 300.
Найти пределы
5.
6.
Провести полное исследование и построить графики функций:
7.
8.
Вычислить
интегралы: 9.
10.
11. Найти
экстремумы функции
.
12. В коробке 10 зеленых и 12 красных пуговицы. На удачу, без возвращения, одна за другой вынимаются 2 пуговицы. Найти вероятность того, что обе пуговицы зеленые.
13. Дан ряд распределения случайной величины X.
X |
4 |
5 |
6 |
10 |
11 |
p |
0,2 |
0,3 |
0,05 |
0,1 |
? |
Построить функцию распределения. Найти математическое ожидание, дисперсию, среднее квадратическое отклонение.
14. Непрерывная случайная величина распределена по экспоненциальному закону с математическим ожиданием, равным восьми (MX=8). Найти вероятность того, что Х примет значение в интервале от 2 до 4-ех. Р(2<X<4)=?.
Вариант № 5