4.3 Преобразования Лоренца

 

Релятивист­ские преобразования координат и времени, отражающие свойства пространства и времени в специальной теории относительности, называются преобразованиями Лоренца. Согласно этим преобразованиям переход от системы К` к системе К осуществляется по формулам (4.9), а от К к системе К` – по формулам (4.10)

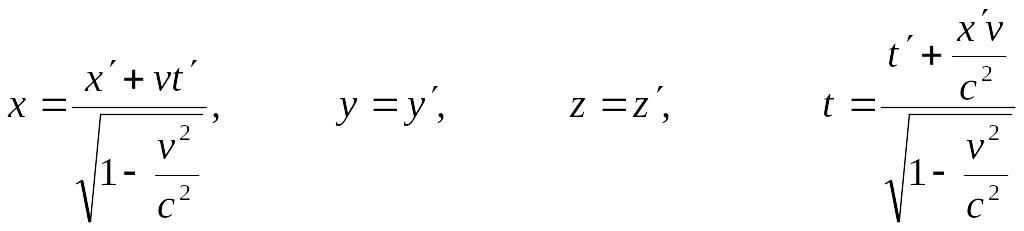. (4.9)

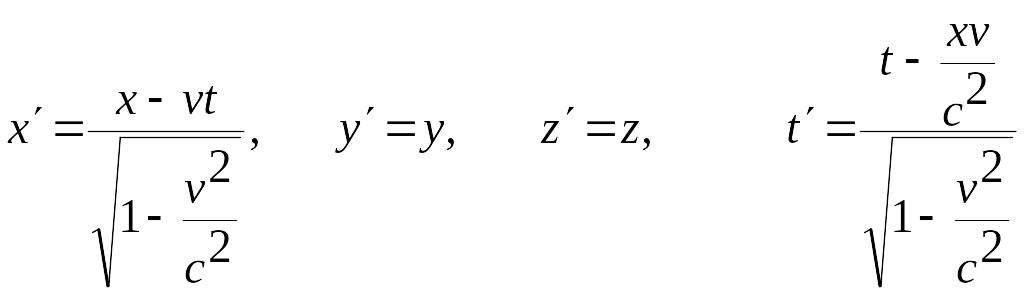(4.10)

 

 

 

На основе полученных преобразований координат и времени можно дать еще одну формулировку принципа относительности: физические законы инвари­антны относительно преобразований Лоренца.

Рассмотрим некоторые следствия из преобразований Лоренца. Во-первых, преобразования Лоренца наглядно демонстрируют неразрывную взаимосвязь пространственных и временных свойств нашего мира. Таким обра­зом, нельзя говорить отдельно о пространстве и отдельно о времени, правильно будет говорить о пространстве – времени, в котором существует наш мир. Иными словами, наш мир четырехмерен.

Во-вторых, на основе преобразований Лоренца можно описать относитель­ность одновременности, о которой мы ранее говорили на качественном уровне.

В-третьих, оказывается, что выражаемый формулой (4.5) классический за­кон сложения скоростей несправедлив при движении тел со скоростями, близ­кими скорости света. Релятивистский закон сложения скоростей для случая, когда частица движется вдоль оси Х

 

(4.11)

 

4.4 Инварианты специальной теории относительности

 

Из преобразований Лоренца следует, что скорость света одна и та же в раз­личных инерциальных системах отсчета. Этот вывод соответствует принципу по­стоянства скорости света. Из формул преобразований Лоренца следует также, что скорость света является максимальной .

В релятивистской механике инвариантность пространственных и времен­ных интервалов относительно преобразований Лоренца не имеет места. Возни­кает вопрос, нельзя ли в специальной теории относительности указать величину, свя­занную с пространственными и временными интервалами между двумя собы­тиями, которая была бы инвариантна преобразованиям Лоренца? Этот вопрос ре­шается положительно. Таким инвариантом в специальной теории относительно­сти является величина , определяемая соотношением

. (4.12)

Эта величина называется пространственно – временным интервалом (или просто интервалом) между событиями.

 

4.5 Элементы релятивистской динамики

 

Релятивистский импульс выражается формулой

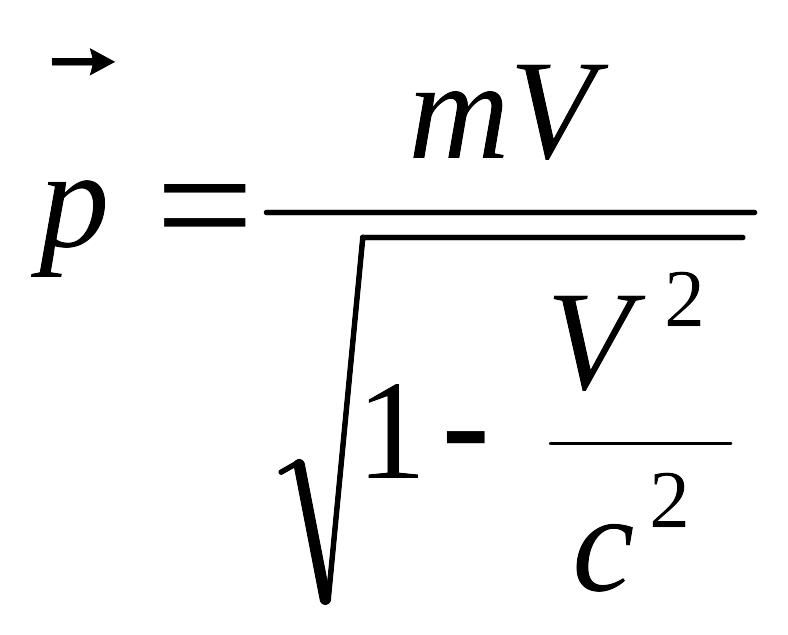. (4.13)

С учетом выражения (4.13) основной закон динамики, представленный соот­ношением

будет справедлив и для релятивистских движений.

В релятивистском законе динамики в общем случае направления векторов и не совпадают; нарушается и пропорциональность между величинами ускорения и силы.

Введем в рассмотрение величину , называемую полной энергией тела

. (4.14)

Полная энергия тела величина сугубо положительная, причем и в состоянии по­коя она не равна нулю. При полная энергия называется энергией покоя

. (4.15)

Формула (4.15) устанавливает взаимосвязь энергии покоя тела и его массы и показывает, что масса и энергия представлены в любом теле в пропорциональных количествах. Каждое изменение энергии покоя тела неизбежно сопровождается пропорциональным изменением его массы.

Полная энергия включает и энергию движения, т.е. кинетическую энергию. Поэтому кинетическая энергия тела определяется как разность между полной энергией и энергией покоя

. (4.16)

Взятые раздельно друг от друга энергия W и импульс р относительны, то есть, различны в разных системах отсчета. Однако взятые совместно в виде ком­бинации они образуют абсолютную характеристику состояния частицы, инвариантную относительно преобразовании Лоренца. Из инвариантности этой величины вытекает релятивистская взаимосвязь между импульсом и энергией – при переходе из одной инерциальной системы в другую, импульс и энергия час­тицы изменяются так, что комбинация остается неизменной.