9 Силовое действие магнитного поля. Работа перемещения проводника с током в магнитном поле

Основные понятия, законы, соотношения.

Сила Лоренца. Сила Ампера.

Магнитный момент витка с током. Момент сил, действующих на виток с током в магнитном поле.

Магнитный поток. Теорема Гаусса.

Работа перемещения проводника с током в магнитном поле.

[1] т. 2 §§ 37-41; [ 2 ] §§ 11 V_t114,120,121.

Основные типы задач по данной теме - это задачи на:

• расчет силового действия магнитного поля и работы по перемещению в нем проводника с током;

• расчет магнитного потока сквозь заданную поверхность.

Задачи первого типа решаются с применением соответствующих формул, выражающих

- силу Лоренца; силу Ампера в интегральной форме (если поле однородное, а проводник - прямолинейный), либо в дифференциальной форме с последующим интегрированием;

- момент силы, действующей на виток с током в магнитном поле; работу силы.

Расчет магнитного потока в общем случае неоднородного поля выполняется в следующей последовательности:

1) на рисунке изобразить линии магнитной индукции заданного по условию задачи поля и контур поверхности, через которую нужно вычислить поток ;

2) выделить бесконечно малый элемент поверхности площадью , таким образом, чтобы во всех его точках величина модуля (или нормаль ной к поверхности проекции ), была бы одинакова. В зависимости от кон фигурации и симметрии поля это может быть, например, узкая прямая по лоска или тонкое кольцо и т.п.;

3) определить, элементарный магнитный поток, пронизывающий вы деленный элемент поверхности, по формуле:

Пример 12.

В одной плоскости с бесконечно длинным прямым проводом, по которому идет ток силы , расположена прямоугольная рамка со сторонами а и b (рисунок 9). Ближайшая из двух, параллельных току, сторон рамки находится на расстоянии . Определить магнитный поток через рамку.

Решение.

1) Индукция магнитного поля В прямого бесконечного провода с током равна по модулю:

;

его линии представляют собой концентрические окружности, центры которых лежат на оси прямого провода.

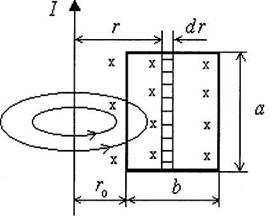2) Разделим площадь рамки на узкие полоски так, чтобы в пределах каждой полоски магнитное поле можно было бы считать однородным. Выделим одну из таких полосок шириной , находящуюся на расстоянии от оси прямого тока.