2) Вспомогательную (гауссову) поверхность выберем в форме цилиндра произвольного радиуса r и длины ℓ, коаксиального с заданным цилиндром (рисунок 4)
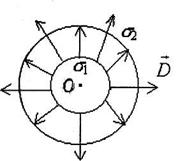
Рисунок 4 Рисунок 5
3) На рисунке 5 изображена картина линий вектора электрического смещения D для случая, когда внутренний цилиндр заряжен положительно, а внешний - отрицательно (σ2 < 0).
4) Поток электрического смещения сквозь выбранную поверхность в нашем случае равен:
ФD = D(r)·2πrℓ, (6.1)
здесь учтено, что линии вектора D пронизывают только цилиндрическую часть поверхности (по радиальным линиям), а через торец вспомогательного цилиндра поток равен нулю, т.к. линии поля лишь скользят вдоль, но не пронизывают его.
5) Величина стороннего заряда Q, охватываемого гауссовой поверхностью, равна:
а) Q = 0, если r < R1 (точка А на рисунке 4);
б) Q = σ1·2πRℓ , если R1 ≤ r ≤ R2 (точка B);
в) Q = (σ1·R1 + σ2·R2)·2πℓ, если r ≥ R2 (точка С).
6) в соответствии с теоремой Гаусса:
0,
r
<
R1
σ1·2πRℓ,
R1
≤
r
≤
R2
(6.2)
σ1·R1 + σ2·R2)·2πℓ, r ≥ R2 .
Таким образом, из (6.2) получим:
0,
r
<
R1
D(r)
=
,
R1
≤
r
≤
R2
(6.3)
r
≥
R2
.
В однородном диэлектрике справедливо:
D = εε0E, (6.4)
откуда
0 , r < R1,
E(r)
=
,
R1
≤
r
≤
R2
,,
(6.5)
,
r
≥
R2.
7 Постоянный ток. Законы постоянного тока
Основные понятия, законы, соотношения
Сила тока. Плотность тока. Классическая электронная теория электропроводности металлов.
Электродвижущая сила. Падение напряжения. Закон Ома для неоднородного участка цепи в интегральной и дифференциальной форме. Работа и мощность тока. Полезная и полная мощность.
[1] т.2 §§ 24,25,26,28, 30; [2] §§ 96-100,102.
Основная задача теории постоянного тока — это расчет электрической цепи, когда задана некоторая произвольная электрическая цепь и отдельные ее параметры, например, ЭДС и сопротивление, и требуется найти силы токов, напряжение на некотором участке цепи, работу, мощность, коэффициент полезного действия и т.п.
Самой
важной фундаментальной величиной в
явлении постоянного тока
служит сила тока
,
поэтому основная задача в теории
постоянного тока
заключается в нахождении токов,
протекающих в цепи. Существуют различные
методы решения этой задачи. В курсе
«физика 1» мы рассматриваем
лишь один из них.
Этот метод основан на последовательном применении закона Ома для замкнутой цепи и закона Ома для неоднородного (или однородного) участка цепи. Применение законов Ома позволяет полностью рассчитать токи в цепи с одним источником ЭДС, либо несколькими источниками ЭДС, соединенными последовательно, а также в тех случаях, когда имеются батареи, состоящие из совершенно одинаковых источников тока. В последнем случае такую батарею в расчетах заменяют одним эквивалентным источником тока (E экв , rэкв).
При последовательном соединении одинаковых источников, ЭДС каждого из которых равна E, а внутреннее сопротивление равно r, параметры эквивалентной батареи вычисляют согласно формулам:
Eэкв = NE, (7.1)
rэкв = Nr. (7.2)
При параллельном соединении одинаковых источников:
Eэкв = E, (7.3)
rэкв = r/N. (7.4)
Пример 11.
Три
группы из двух последовательно
соединенных одинаковых элементов
соединены параллельно. ЭДС каждого
элемента
,
внутреннее сопротивление
.
Полученная батарея замкнута на внешнее
сопротивление
.
Найти силу тока во внешней цепи.
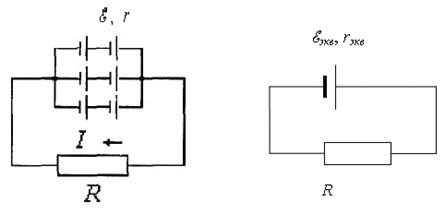
Рисунок 6 Рисунок 7
Решение.
Электрическая
схема заданной цепи изображена на
рисунке 6. Преобразуем эту схему в более
простую. Для этого сначала заменим
группу из двух последовательно
соединенных элементов одним эквивалентным
источником с
,
.
Три таких источника, соединенных
параллельно, в свою очередь, можно
заменить одним эквивалентным
источником с параметрами:
,
.
Получается, таким образом, очень простая эквивалентная схема (рисунок 7). Согласно закону Ома для замкнутой цепи:
.
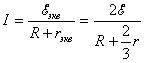Произведя
вычисления, получим искомый ответ:
.