Расчет термических напряжений

ОПРЕДЕЛЕНИЕ. Необходимым и достаточным условием возникновения термических напряжений является наличие разности температур на разных поверхностях тела.

Используя инженерную методику расчета Н.Ю. Тайца , в основе которой лежит квазистатическая несвязанная модель при независимости от температур теплофизических и механических свойств, запишем для плоской стенки термические напряжения

с горячей , Па (1.21)

и холодной стороны , Па, (1.22)

где и - температуры на горячей (левой) и холодной (правой) стороне поверхности, - удельное напряжение, приходящиеся на 1 градус температуры, Па/К;

- линейный коэффициент расширения, 1/К;

Е – модуль упругости Юнга, Па;

v - коэффициент Пуассона.

Для плоских стенок или при линейном распределении температур вдоль стенки среднемассовая температура совпадает со среднеарифметической, т.е (1.13)

1.5.2. Теплопроводность плоской многослойной стенки.

Дано: число слоев m, режим стационарный

Известны: t_n1 и t_{n нар} (Рис. 1.6)

Найти: тепловой поток q и температуры в любой точке многослойной стенки.

Решение.

Пользуемся случаем, что .

Рис. 1.6. Теплопроводность плоской многослойной стенки

Запишем тепловые потоки для каждой стенки согласно уравнению (1.20) , найдем разность температур

,

………………………………………………………….

, .

О пределив t – (температурные напоры) и сложив левые и правые части полученных уравнений, будем иметь .

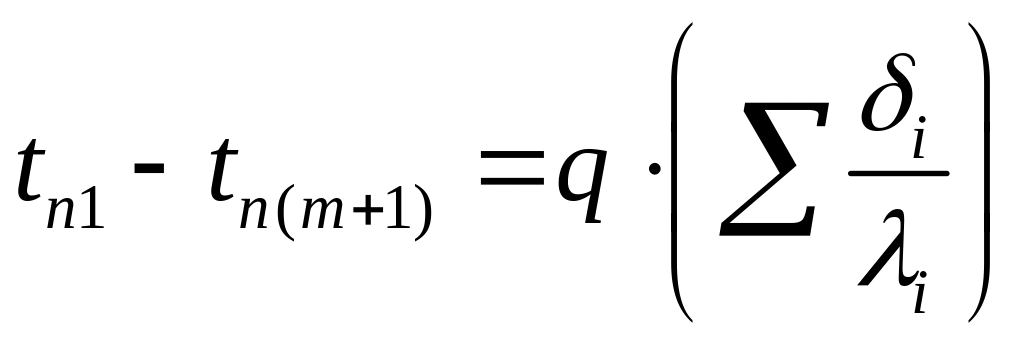– полное термическое сопротивление многослойной стенки равное сумме R_Т всех слоев. Тогда удельный тепловой поток через многослойную стенку

. (1.21)

Уравнение (1.21) впервые получил в 1807 г. Фурье. Анализируя это выражение и используя аналогию между протеканием теплоты и электричества, Ом получил свой закон для расчета силы тока как частное от деления разности электрических потенциалов (падения напряжения на концах проводника) на электрическое сопротивление R, т.е. .

Зная q, найдем температуры в местах контакта стенок t_ni : и т.д. .

Поле температур внутри каждой пластины можно рассчитать по полученному ранее решению (1.19), полагая начало координат на левой стороне соответствующей пластины.

Средняя температура многослойной стенки может быть представлена как среднеарифметическая от средних температур каждой стенки:

1.5.3. Теплопередача через плоскую однослойную стенку

ОПРЕДЕЛЕНИЕ. Передача тепла от одной более горячей среды (жидкости или газа) к другой холодной , через разделяющую их одно или многослойную стенку любой формы называется теплопередачей.

ФИЗИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ.

Известны, в отличие от предыдущей задачи, температуры не на поверхности стенки, а температуры окружающей среды вдали от поверхностей t_ж.1 слева и t_ж.2 – справа, а также коэффициенты теплоотдачи ₁ и ₂. Требуется найти поле температур и тепловой поток через стенку (рис.1.7).

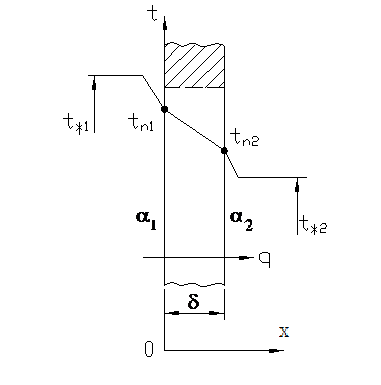
Рис. 1.7 Теплопередача через плоскую стенку

Воспользуемся случаем, что при .

Из выражений тепловых потоков, найдем разности температур, просуммируем левые и правые части и после несложных преобразований, получим

Тогда , (1.22)

где – коэффициент теплопередачи, характеризует интенсивность передачи теплоты от одной жидкости к другой через разделяющую их стенку.

- полное термическое сопротивление, м² К/Вт;

- термическое сопротивление горячей среды; -- тоже, теплопроводности стенки; - холодной жидкости.

Зная q, найдем температуры на поверхностях: ;

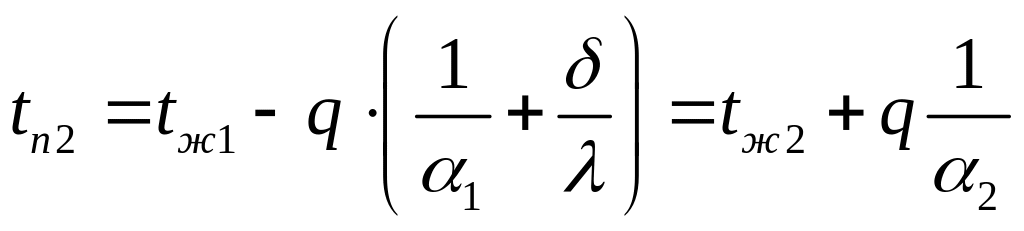. (1.23)