1.4.2. Краевые условия.

Уравнение (1.5) описывает процесс теплопроводности в самом общем виде, т.е. описывает целый класс явлений теплопроводности.

Пример: Пусть дано дифференциальное уравнение , его решение: , где С – постоянная интегрирования. Это набор прямых линий. Если уравнение 2-го порядка, то возникнут две постоянные и т.д. Для определенности решения нужно добавить краевые условия (КУ) или условия однозначности.

Определение.

КУ – это частные особенности, которые совместно с дифференциальным уравнением дают полное математическое описание конкретного процесса. Следует различать условия однозначности:

1) геометрические –– должны быть заданы форма и размеры тела;

2) физические , с, , q_v(x,) и др.

3) начальные (временные) если , то задается начальное распределение температуры .

Часто принимают .

4. Граничные условия (ГУ) – характеризуют взаимодействие тела с окружающей средой.

Существует несколько способов задания граничных условий:

ГУ I pода - задано распределение температур на поверхности:

, часто .

ГУ II pода - задан тепловой поток на поверхности

; т.е. .

Часто полагают . Например, первый период нагрева металла в нагревательных колодцах.

ГУ III pода - Заданы температура окружающей среды и закон теплообмена между средой и поверхностью тела. Чаще всего используется закон Ньютона-Рихмана:

q_пов=q_конв., т.е. ,

где - коэффициент теплоотдачи Вт/м²К, характеризует интенсивность теплоотдачи между поверхностью тела и окружающей средой.

; .

Для высокотемпературных процессов должен учитываться нагрев тел излучением

или .

ГУ IV рода – когда заданы температуры и тепловые потоки в местах контакта двух разных тел:

.

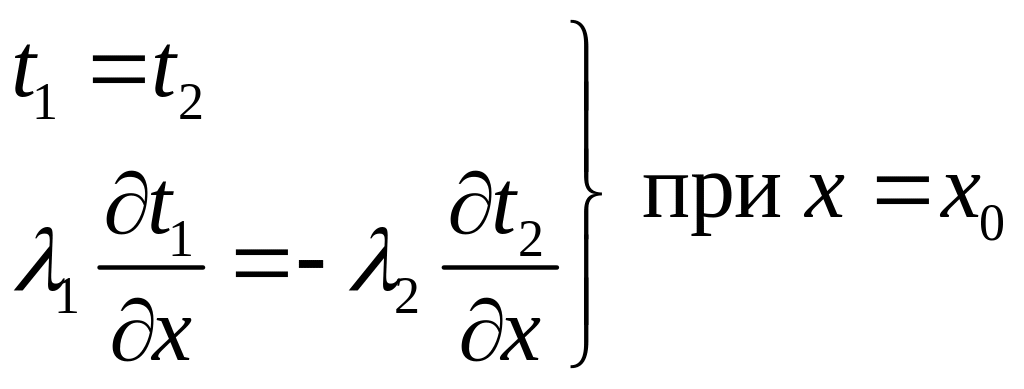Рис. 1.4. К граничным условиям четвертого рода

Дифференциальное уравнение совместно с условием однозначности дают полную математическую формулировку задачи теплопроводности, т.е. задачи нахождения температурного поля в твердом теле.

Эта задача может быть решена:

1. экспериментально; 2) теоретически.

Приведем порядок (алгоритм) решения любой задачи (проблемы).

1. Ставится ФПЗ (физическая постановка задачи). Дано – найти. Цель.

2. Проводится обзор работ, патентно-информационный поиск (ПИП). Наброски математической модели.

3. Ставится МПЗ (математическая постановка задачи). Проводится анализ МПЗ.

4. Выбор и обоснование метода решения. АВМ, ЭЦВМ, эксперимент – что есть в наличии.

5. Решение задачи.

6. Анализ полученного решения

7. Выводы и рекомендации.

5. Стационарная теплопроводность

Рассмотрим наиболее простые случаи.

1.5.1. Теплопроводность плоской однослойной стенки

а) физическая постановка задачи. Пусть дана неограниченная плоская однослойная стенка толщиной  (Рис.1.5).

Рис. 1.5 Теплопроводность в плоской стенке

Пусть коэффициент теплопроводности . Известны температуры на левой поверхности t_п.1, а на правой – t_п.2, которые не изменяются со временем. Внутренние источники теплоты отсутствуют, т.е. q_V= 0. Тепловые потоки вдоль осей OY и OZ отстутсвуют. Тогда .

Задача: Требуется найти распределение температур по сечению t(x) и тепловой поток q через стенку.

б) математическая постановка: для расчета процесса теплопроводности следует использовать дифференциальное уравнение (1.7) в декартовой системе координат. Заменим на d , т.к. стенка плоская и температура зависит только от одной переменной х. Учтем, что температуры неизменны во времени, т.е.

; (1.15)

; (1.16)

. (1.17)

Система уравнений (1.15)…(1.17) представляет собой математическую постановку задачи теплопроводности в плоской стенке.

Решение диференциального уравнения (1.15): ; (1.18)

С помощью граничных условий (1.16) и (1.17) найдем постоянные и . Полагая в уравнении (1.16) х=0 , получим , затем х= в (1.17). Тогда .

Подставляя в (1.18) и , получим , (1.19)

где ;

Анализ полученного решения.

. Температура согласно (1.19) меняется вдоль стенки по линейному закону.

Весьма удобно представить решение в безразмерном виде: , где , ; , т.е. отсчет ведем от наименьшей температуры.

2. Тепловой поток согласно закону Фурье: ,

, (1.20)

где м²К/Вт – термическое сопротивление плоской стенки.

3) . Другой вид решения (1.19)

4) Полное количество теплоты , Дж.

5) Если учесть зависимость коэффициента теплопроводности, например, пусть изменяется по линейному закону , тогда решение будет иметь вид

,

где 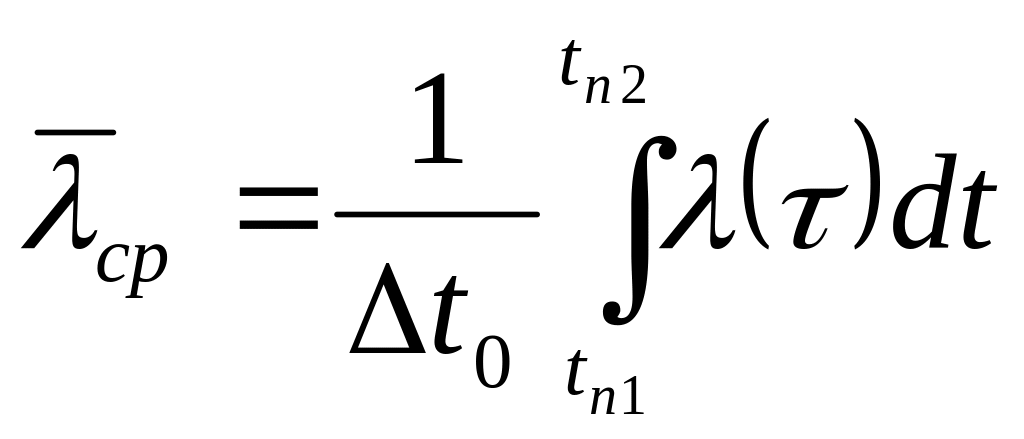- средний коэффициент теплопроводности.

Распределение температур – уже будет не прямая, а кривая линия (см. пунктирную линию на рис. 1.5.).