1.4. Дифференциальное уравнение теплопроводности

При решении задач, связанных с нахождением температурного поля, необходимо иметь дифференциальное уравнение теплопроводности. Для сложных физических явлений, когда исходные величины могут существенно меняться в пространстве и времени на помощь приходит метод математической физики. Сущность метода: ограничивается отрезок времени от  до +d и из всего пространства V выделяется элементарно малый объём тела dV.

Вывод уравнения основывается на законе сохранения энергии или I-м законе термодинамики, записанного для dV и d. Получим уравнение в декартовой системе координат, тогда .

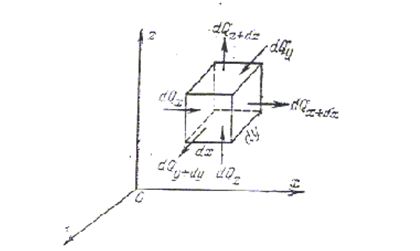
Рис. 1.3. К выводу диференциалоного уравнения теплопроводности

Полное количество теплоты, полученное телом

Q=cmΔt=cρVΔt или в дифференциальном виде dQ₁=cρdVdT где Δt=t_конечн-t_нач=(t+dt)-t=dt. С другой стороны, используя понятие удельного теплового потока вдоль оси Х

dQ₂=qdFd, где ∆q=q_x-(q_x+dq_x)=-dq_х. Согласно закону сохранения энергии должно быть Q₁=Q₂ или тепловой баланс в дифференциальной форме: . Учтя, что , разделив уравнение на dV и d и используя закон Фурье: и т.д., получим

(1.5)

или в более компактном виде

,

где div – «дивергенция»- термин векторной алгебры

Если внутри тела действуют источники (стоки) теплоты, то в правую часть уравнений добавляется величина q_V – объемная плотность внутренних тепловыделений (теплопоглощений)

, Вт/м³.

1.4.1. Анализ дифференциального уравнения теплопроводности

Оно устанавливает связь между временным () и пространственным изменением температуры в любой внутренней точке тела, в которой происходит процесс теплопроводности.

Для простоты анализа примем, что тело изотропное, когда его теплофизические свойства не зависят от направления. Пусть также коэффициент теплопроводности не зависит от температуры. Тогда и уравнение теплопроводности (1.5) упрощается

. (1.6)

Существует более компактная форма записи дифференциального уравнения теплопроводности

(1.7)

где – лапласиан, Набла в квадрате или оператор Лапласа в декартовой системе координат; - коэффициент температуропроводности, м²/с.

Запись оператора Лапласа в других системах координат:

а) цилиндрическая: , (1.8)

б) сферическая: , (1.9)

где  - азимутальный угол или угол долготы (меридианы),  - угол широты (параллели) цилиндрической и сферической систем координат.

Для одномерного поля температур можно записать общее уравнение:

(1.10)

где k – фактор геометрической формы равный 1 – для плоского тела, 2 – цилиндра и 3 для шара.

Рассмотрим физический смысл коэффициента температуропроводности а.

1. это физический параметр, зависящий от рода вещества и в основном от температуры;

2. существенен только для нестационарных процессов;

3. характеризует скорость изменения температуры, т.е. а – представляет меру теплоинерционных свойств. Это вытекает из уравнения (1.7), т.к. то скорость изменения температуры будет тем больше, чем больше а. Т.е. выравнивание температур будет быстрее происходить в том теле, где температуропроводность больше.

Т.к. , то можно составить такую "цепочку" неравенств:

а_{металлов}а_{жидкости}а_газов

Анализ 1) Пусть . Получим уравнение Фурье : ; (1.11)

2) , уравнение Пуассона; (1.12)

3) , уравнение Лапласа. (1.13)

В уравнениях (1.12) и (1.13) температуропроводность отсутствует, т.е.

4) ;

когда , то получим одномерное уравнение . (1.14)

Нахождение решений этих уравнений в частных производных представляет собой основное содержание теории теплопроводности.