1. Теплопроводность

1.1 Температурное поле

Температурное поле – это совокупность значений температур в данный момент времени  для всех точек изучаемого пространства. Математическая запись: t=f(x,y,z,). (Бывают поля скоростей, давлений, напряжений, концентраций, электрические, магнитные, электромагнитные, гравитационные, биополя и т.д.) Изложенные ниже основы расчета температурных полей могут быть применены к расчету других полей. t=f₃(x)одномерное стационарное температурное поле. Возможны случаи, когда t=f₂(x,y) – двухмерное стационарное, а если t=f₄(x,) – одномерное нестационарное, а при t=f₅() – нольмерное нестационарное, это нагрев термически тонкого тела.

Определение 1. Изотермическая поверхность – это геометрическое место точек, имеющих одинаковую температуру.

Свойства изотерм: изотермы не должны пересекаться, это функция однозначная, т.к. одна и та же точка не должна иметь две разные температуры

1.2. Градиент температур.

, град/м. Градиент температур - это предел отношения изменения температуры к расстоянию между изотермами по нормали n.

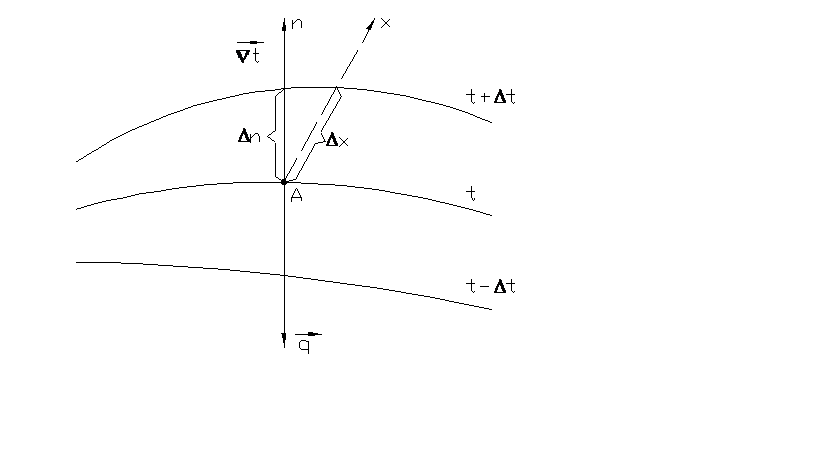
Рис. 1.1 Изотермы и градиент температур

(1.1)

t- это вектор, направленный в сторону возрастания температур (или другой величины).

Второе определение. Температурный градиент представляет собой максимальное изменение температуры на единицу длины в направлении нормали n к изотерме. и т.д. Пример: слиток .

1.3. Основной закон теплопроводности.

Постулат Фурье о пропорциональности теплового потока градиенту: q~grad←t после многочисленных опытных проверок превратился в Закон, названный его именем: , Вт/м². (1.2)

Закон Фурье (1.2) называют основным законом теплопроводности.

Для одномерного стационарного поля температур закон Фурье упрощается до вида:

(1.3)

Так как тепловой поток является вектором, то его можно записать в проекциях на оси x,y,z:

.

Знак " –" поставлен из тех соображений, что тепловой поток, будучи вектором, направлен в сторону убывания температуры, т.е. в противоположную сторону чем градиент температур.

Полное количество теплоты найдем путем интегрирования по поверхности и времени следующего выражения: ,

Тогда , Дж (1.4)

–это коэффициент пропорциональности в законе Фурье, показывает какое количество тепла передается в 1^цу времени при градиенте t=1⁰/м, [] = = Вт/мК. Коэффициент теплопроводности –характеризует способность тела проводить теплоту.  - это физический параметр, зависящий от природы тела, температуры, давления (для газов) и от направления (для анизотропных тел), например: древесина, материалы в рулонах и т.д. Существует тесная аналогия между протеканием электричества и теплоты. Поэтому хорошие проводники электричества (золото, серебро, платина медь) одновременно являются хорошими проводниками теплоты. Коэффициенты теплопроводности таких тел Вт/мК, для других тел см. рис. 1.2.

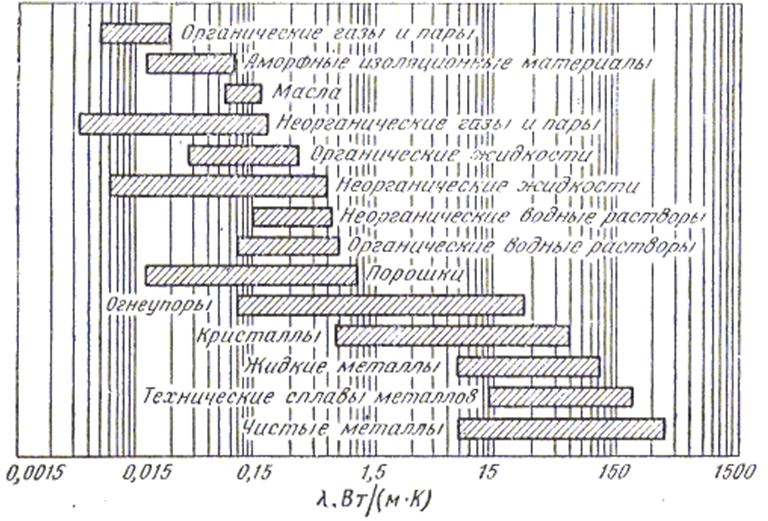
Рис. 1.2 Порядок значений коэффициентов теплопроводности различных веществ